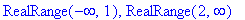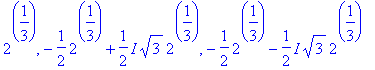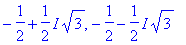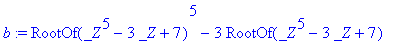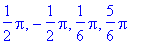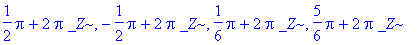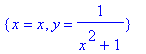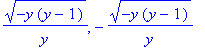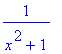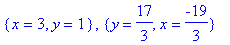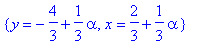rootof в maple что это

Rootof в maple что это

уМЕДХАЭБС: task2, рТЕДЩДХЭБС: Top, чЧЕТИ: Top

1 уЙУФЕНЩ ЛПНРШАФЕТОПК БМЗЕВТЩ

Maple – УРЕГЙБМЙЪЙТПЧБООЩК НБФЕНБФЙЮЕУЛЙК РБЛЕФ, ЛПФПТЩН РПМШЪХАФУС РТПЖЕУУЙПОБМШОЩЕ НБФЕНБФЙЛЙ ЧП ЧУЕН НЙТЕ. рПДПВОЩЕ РБЛЕФЩ ФБЛЦЕ ОБЪЩЧБАФУС УЙУФЕНБНЙ ЛПНРШАФЕТОПК БМЗЕВТЩ. йЪ НОПЦЕУФЧБ РПДПВОЩИ УЙУФЕН (Maple, Matlab, Mathcad, Mathematica, Macsyma, Derive, Axiom, MuPAD) Maple СЧМСЕФУС РТЙЪОБООЩН МЙДЕТПН Ч ПВМБУФЙ УЙНЧПМШОЩИ ЧЩЮЙУМЕОЙК (ФП ЕУФШ Ч РТЕПВТБЪПЧБОЙЙ ЧЩТБЦЕОЙК У ЙУРПМШЪПЧБОЙЕН РЕТЕНЕООЩИ, НОПЗПЮМЕОПЧ, ЖХОЛГЙК Й Ф.Д.). рПНЙНП ЬФПЗП Ч Maple ЧИПДСФ НПДХМЙ, ПВМЕЗЮБАЭЙЕ ТБВПФХ Ч ФБЛЙИ ТБЪДЕМБИ НБФЕНБФЙЛЙ, ЛБЛ ЧЩУЫБС БМЗЕВТБ, МЙОЕКОБС БМЗЕВТБ, БОБМЙФЙЮЕУЛБС ЗЕПНЕФТЙС, ФЕПТЙС ЮЙУЕМ, НБФЕНБФЙЮЕУЛЙК БОБМЙЪ, ДЙЖЖЕТЕОГЙБМШОЩЕ ХТБЧОЕОЙС, ЛПНВЙОБФПТОЩК БОБМЙЪ, ФЕПТЙС ЧЕТПСФОПУФЕК, УФБФЙУФЙЛБ Й НОПЗЙИ ДТХЗЙИ.

Maple ЛБЛ УХРЕТЛБМШЛХМСФПТ

ч ТБВПЮЕН МЙУФЕ (worksheet) УЙУФЕНЩ Maple НПЦОП ЧЧПДЙФШ ЛПНБОДЩ РПУМЕ РТЙЗМБЫЕОЙС » > «. лПНБОДБ ДПМЦОБ ЪБЧЕТЫБФШУС УЙНЧПМПН » ; «, ЕЕ ТЕЪХМШФБФ ОЕНЕДМЕООП ЧЩЧПДЙФУС ОБ ЬЛТБО. еУМЙ ЧНЕУФП » ; » РПУФБЧЙФШ » : «, ФП ЛПНБОДБ ВХДЕФ ЧЩРПМОЕОБ, ОП ТЕЪХМШФБФ ЕЕ ТБВПФЩ ОЕ ВХДЕФ ОБРЕЮБФБО. оБРТЙНЕТ:

уЙНЧПМ % ПВПЪОБЮБЕФУС РПУМЕДОЕЕ ЧЩЮЙУМЕООПЕ Maple ЧЩТБЦЕОЙЕ, %% – РТЕДРПУМЕДОЕЕ, %%% — РТЕДРТЕДРПУМЕДОЕЕ (Б ЧПФ ПВПЪОБЮЕОЙС %%%% ХЦЕ ОЕ УХЭЕУФЧХЕФ).

юЙУМБ Й ЛПОУФБОФЩ

еУМЙ Ч ЧЩТБЦЕОЙЙ ЧУФТЕЮБЕФУС ЮЙУМП, ЪБРЙУБООПЕ У РМБЧБАЭЕК ФПЮЛПК (ОБРТЙНЕТ, 3.14 ЙМЙ 5.6e-17 ), ФП ЧУЕ ЧЩЮЙУМЕОЙС ЧЩРПМОСАФУС РТЙВМЙЦЕООП, Ч РТПФЙЧОПН УМХЮБЕ ЧЩЮЙУМЕОЙС РТПЧПДСФУС ФПЮОП. ч Maple ЕУФШ УМЕДХАЭЙЕ ЛПОУФБОФЩ: Pi юЙУМП РЙ
I нОЙНБС ЕДЙОЙГБ i
exp(1) пУОПЧБОЙЕ ОБФХТБМШОЩИ МПЗБТЙЖНПЧ e
infinity вЕУЛПОЕЮОПУФШ
true мПЗЙЮЕУЛБС ЙУФЙОБ
false мПЗЙЮЕУЛБС МПЦШ

чЩЮЙУМЕОЙС У ХЮБУФЙЕН ЛПОУФБОФ ЧЩРПМОСАФУС ФПЮОП (ЕУМЙ ФПМШЛП ЙИ ЪОБЮЕОЙЕ ОЕ ВХДЕФ РЕТЕЧЕДЕОП Л ДЕКУФЧЙФЕМШОПНХ ЪОБЮЕОЙА), ОБРТЙНЕТ

пРЕТБФПТЩ

ч Maple УХЭЕУФЧХАФ УМЕДХАЭЙЕ ПРЕТБФПТЩ:

рЕТЕНЕООЩЕ

уФБОДБТФОЩЕ ЖХОЛГЙЙ

рТЕПВТБЪПЧБОЙЕ НБФЕНБФЙЮЕУЛЙИ ЧЩТБЦЕОЙК

ч ЧЩТБЦЕОЙЕ НПЗХФ ЧИПДЙФШ ЛПОУФБОФЩ, УЧПВПДОЩЕ РЕТЕНЕООЩЕ, НБФЕНБФЙЮЕУЛЙЕ ЖХОЛГЙЙ. рТЙНЕТ ЧЩТБЦЕОЙС:

дПЧПМШОП ЮБУФП Ч ЛБЮЕУФЧЕ ЧЩТБЦЕОЙК ЧЩУФХРБАФ НОПЗПЮМЕОЩ ПФ ПДОПК ЙМЙ ОЕУЛПМШЛЙИ РЕТЕНЕООЩИ ЙМЙ ТБГЙПОБМШОЩЕ ЧЩТБЦЕОЙС. Maple УПДЕТЦЙФ ТБЪМЙЮОЩЕ ЖХОЛГЙЙ ДМС РТЕПВТБЪПЧБОЙС ФБЛЙИ ЧЩТБЦЕОЙК.

жХОЛГЙС factor(eq) ТБЪМБЗБЕФ ЧЩТБЦЕОЙЕ eq ОБ НОПЦЙФЕМЙ.

тЕЫЕОЙЕ ХТБЧОЕОЙК

пВЩЛОПЧЕООЩЕ ХТБЧОЕОЙС

уЙУФЕНЩ ХТБЧОЕОЙК

юЙУМЕООПЕ ТЕЫЕОЙЕ ХТБЧОЕОЙК

йОПЗДБ Maple РТЙ ТЕЫЕОЙЙ ФТБОУГЕОДЕОФОЩИ ХТБЧОЕОЙК ОЕ ЧЩЧПДЙФ УМПЦОЩЕ ЧЩТБЦЕОЙС Ч ЧЙДЕ ТБДЙЛБМПЧ, Б ПУФБЧМСЕФ ЙИ Ч ЖПТНЕ RootOf. юФПВЩ ЪБУФБЧЙФШ Maple ЧЩЧПДЙФШ ЧУЕ ТЕЫЕОЙС Ч ЧЙДЕ ТБДЙЛБМПЧ (ЕУФЕУФЧЕООП, ЕУМЙ ПОЙ РТЕДУФБЧЙНЩ Ч ФБЛПК ЖПТНЕ), ОЕПВИПДЙНП РТЙУЧПЙФШ ЪОБЮЕОЙЕ true УЙУФЕНОПК РЕТЕНЕООПК _EnvExplicit ( _EnvExplicit:=true ).

тЕЫЕОЙЕ ФТЙЗПОПНЕФТЙЮЕУЛЙИ ХТБЧОЕОЙК

Источник

Решение уравнений

Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений

Уравнения с одной переменной

Для решения таких уравнений в Maple предусмотрены две команды: solve для символьного решения и fsolve для решения с ответом в численном виде. Например, формула для квадратного уравнения:

Maple знает формулы для кубического уравнения:

но они сложны, неприятны по внешнему виду, и их почти никогда не применяют.

Используем численные коэффициенты, чтобы ответ был численным:

Этот результат – правильный, но поскольку Maple «думает» символами, то они не выглядят слишком пригодными. Для получения чисел с плавающей запятой следует применять уже известную команду evalf :

или вводить коэффициенты уравнения с десятичной точкой:

Команда solve с полиномами работает по-умному: она знает фундаментальную теорему алгебры о том, что полином n-го порядка имеет n корней. Например, если спросить о корнях уравнения x 6 + 1:

в ответе должны быть все шесть.

Maple может решать более сложные уравнения вроде cos(x) – x/10:

При решении сложных уравнений надо проявлять осторожность, поскольку возможно более одного ответа, и Maple не даст все. Попробуем нарисовать функцию cos(x) – x/10 и увидим, как много у нее нулей, т. е. столько корней придется искать.

Maple на самом деле не обманывает: 1.427551779 есть решение, но не все.

Важно: прежде чем искать решение, постройте график, тогда будете знать, сколько корней надо найти.

Посмотрите, что произойдет, если указать диапазон, где нет корней:

По общему правилу, когда Maple без вычислений возвращает то, что ему задали, это означает, что либо он не может найти ответ, либо вы ошиблись. Ищите, где ошибка.

Учтите, что вместо диапазона можно просто задать одно угаданное решение:

Здесь надо быть осторожным. Если для fsolve подсказано начальное значение, причем оно расположено близко к максимуму функции, нули которой ищутся, то fsolve может ошибиться или может найти решение не в том месте, где начальная подсказка. Посмотрим на примере метода секущих, почему так происходит:

Ищем решения уравнения cos(x) + x/3. Чтобы узнать, где искать корни, нарисуем функцию и увидим рядом с 3 два близко расположенных корня. Команда найдет один из них:

а вам нужен второй, и возникает проблема: как указать команде на него или как задать начальное значение. Можно так: ищи один корень вблизи 3, но не ищи s1:

(a) Найдите все решения уравнения e x = 10sin(x) между –5 и 20.

(b) Найдите все решения уравнения e (–x) = x, используйте solve и fsolve и сравните ответы.

(с) Найдите все корни функции для x между 0 и 10.

Эту задачу можно решить очень компактно с помощью команды seq с командой fsolve внутри нее.

Решение разбейте на части:

Шаг 1. Нарисуйте функцию между 0 и 100, затем несколько раз обновите диапазон графика, чтобы узнать, где первый и второй корни и как далеко они друг от друга (вы обнаружите, что они на расстоянии порядка π).

Источник

Rootof в maple что это

Будучи системой символьных вычислений, Maple должен иметь средства для преобразования алгебраических выражений: приведения подобных членов (это делается по умолчанию), раскрытия скобок (expand), группировки (collect), разложения на множители (factor для многочленов и ifactor для целых чисел) упрощения выражений (simplify) и т.д. Действие перечисленных выше функций станет понятно из следующих примеров:

(23) (521) (93799610095769647)

Решение уравнений, неравенств и систем

Для решения уравнений, систем уравнений и неравенств в Maple используется команда (функция) solve. Приведем примеры:

Обратите внимание: если первый (а в нашем случае и единственный) аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0.

Обратите внимание, что открытый интервал (или луч) задается в Maple с помощью функции Open, применяемой к концам интервала, задаваемого функцией RealRange. Не забудьте, что Maple чувствителен к регистру: команда open (с маленькой буквы) служит для открытия файлов.

Рассмотрим примеры решения алгебраических уравнений степеней выше второй:

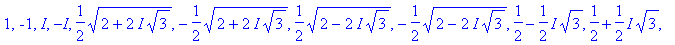
Если же корни уравнения не выражаются в радикалах или их выражение слишком громоздко, Maple представляет ответ, используя функцию RootOf :

В случае, когда корни выражаются в радикалах (например, при решении алгебраических уравнений 4-й степени) получить явное выражение корней можно, присвоив зарезервированной переменной _EnvExplicit значение true. (Альтернативные вариант: использовать функцию convert с параметром radical.)

С помощью команды solve можно решать не только алгебраические уравнения и неравенства:

Приведем ряд примеров применения функции solve для решения уравнений с несколькими переменными:

Приведем примеры решения систем уравнений:

Волгоградский государственный педагогический университет
Кафедра алгебры, геометрии и информатики

Источник

Иллюстрированный самоучитель по Maple 6/7

Решение уравнений и неравенств

Решение систем нелинейных и трансцендентных уравнений

Функция solve может использоваться для решения систем нелинейных и трансцендентных уравнений. Для этого система уравнений и перечень неизвестных задаются в виде множеств.

Ниже приведены примеры решения уравнений:

В этих примерах хорошо видна техника работы с функциями solve и assign. В конце примеров показано восстановление неопределенного статуса переменных х и у с помощью функции unassign и снятие определения переменных с помощью заключения их в прямые апострофы.

Функция RootOf

В решениях уравнений нередко появляется функция RootOf, означающая, что корни нельзя выразить в радикалах. Эта функция применяется и самостоятельно в виде RootOf(ехрr) или RootOf(ехрr, х), где ехрr – алгебраическое выражение или равенство, х – имя переменной, относительно которой ищется решение.

Если х не указана, ищется универсальное решение по переменной _Z. Когда ехрr задано не в виде равенства, решается уравнение ехрr=0. Для получения решений вида RootOf в явном виде может использоваться функция all values.

Примеры применения функции RootOf:

Итак, функция RootOf является эффективным способом представления решения в компактном виде. Как уже отмечалось, наряду с самостоятельным применением она часто встречается в составе результатов решения нелинейных уравнений.

Источник

Символьная алгебра

Справочник символьной математики Maple. Команды, которые нужны для хорошей работы

Описания команд

Maple почти никогда не дает в точности то, что хочется, поэтому придется всегда работать с какими-то ручными алгебраическими выкладками. Однако возможности редактирования (обычные копирование-вставка Ctrl-c и Ctrl-v) позволяют удобно сочетать возможности рабочего листа Maple и алгебраических выкладок «вручную».

Примеры того, что может команда expand (разложить):

Эта команда – вторая половина универсальной Maple-овской пары, применяемой для алгебраических упрощений.

Если в результате расчетов получается алгебраическое выражение, которое требует помощи, пробуйте применять эту комбинацию.

Иногда не срабатывает. Тогда попытайтесь применить expand и simplify :

Бывают случаи, когда вы сами не понимаете, чего хотите.

Поиграйте с этими командами, чтобы хорошо овладеть работой с ними. При этом всегда пытайтесь прежде всего использовать опцию symbolic :

(Обратите внимание, что боковики должны записываться внутри фигурных скобок.) Для Maple это не то же самое, что замена (см. команду subs ниже):

Использование боковиков – это своего рода умная замена, в которой Maple пытается заменить все, что может, используя заданное ему соотношение. Боковик помещается в фигурные скобки, причем можно определить сразу несколько величин в конструкции simplify(expression,);

sort располагает выражения, в особенности полиномиальные, в порядке от высшей степени к низшей:

factor пытается записать полиномы как произведение членов:

Если надо собрать больше, чем один множитель, дайте список множителей в collect :

Укажите отличия между следующим выражением и тем, что написано выше:

Если Maple задано не имеющее решения уравнение, то он возвратит его или не даст ответ. Обратите внимание, что нарисованная ниже функция никогда не становится больше 1.

так что бесполезно пытаться найти, где она равна 2:

Maple не может его решить, поэтому возвращает без ответа.

Нормальная форма рациональных функций для общего знаменателя:

А что получится, если попытаться разложить результат?

Maple разрешает сослаться непосредственно на числитель или знаменатель дробного выражения вроде такого:

но, возможно, не точно в ожидаемой форме. Контролируют части таких выражений, применяя копирование-вставку:

Используйте мышь для выделения числителя выражения (выше), копируйте его с помощью (Ctrl-c), затем вставьте в группу с помощью (Ctrl-v):

Эта команда выбирает части выражения.

Поэкспериментируйте с ней:

Эта команда заменяет одну переменную на другую:

При использовании subs вы, возможно, разочаруетесь ее глупостью:

Ниже приведены несколько полезных примеров-опций.

Примеры применения convert:

Преобразуйте ответ из команды RootOf в вид с квадратными корнями, кубическими корнями и т. п.:

Обратите внимание, что здесь команда convert менее полная, чем allvalues :

Число в конце команды говорит Maple о том, какой корень вы хотите найти. Преобразуем ряд Тейлора в полином с помощью опции polynom

Преобразуем рациональные функции в дробь с помощью опции parfrac :

Преобразуем рациональные функции в непрерывную дробь с помощью confrac :

Выразим функции в экспоненциальной форме с помощью exp :

Преобразуем выражения с синусами и косинусами в форму с тангенсами с помощью tan :

Преобразуем выражения с тангенсами в форму с синусами-косинусами с помощью sincos :

Преобразуем английские меры в метрические convert(…,metric) :

Посмотрим, как английские меры преобразуются в метрические:

Например, convert дает красивое определение функции signum :

Преобразуем комплексное выражение в форму polar :

Но это, вероятно, не в точности то, что имелось в виду. К счастью, команда map сможет представить это в более приемлемом виде.

Эти два аргумента не обязательны, и convert выберет соответствующее количество членов ряда. Ниже несколько примеров с иллюстрирующими графиками, использующих taylor для генерации ряда.

Приближенная функция для синуса. Сравните точный результат (красным) с рациональным приближением (синим):

Это выглядит несколько странно. Почему надо строить приближение имеющейся функции рациональной функцией?

Вот как строится аппроксимация функции Бесселя J 0 (x):

Или иначе, постройте график разности между точной функцией и приближенной. Тогда лучше видна область применимости:

Источник