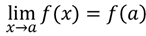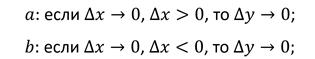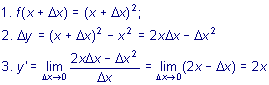Что значит приращение функции

Приращение аргумента, приращение функции

Урок 37. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Приращение аргумента, приращение функции»

· познакомиться с понятием непрерывной функции;

· познакомиться с понятием предел функции в точке;

· рассмотреть примеры использования данных понятий для решения задач.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Не всегда нам надо знать точные значения тех или иных параметров. Иногда нам достаточно знать, как они изменяются. Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на сколько именно изменилась температура воздуха, а нам важно похолодало или потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а важно определить разгоняется автомобиль или тормозит.

Причём, если на улице потеплело, то изменения будут со знаком плюс и наоборот если похолодало, то изменения будут со знаком минус.

Если автомобиль разгоняется, то изменения будут со знаком плюс, если тормозит – то со знаком минус.

Для описания таких изменений было введено понятие приращение.

Приращение аргумента обозначают так:

Приращение функции обозначают так:

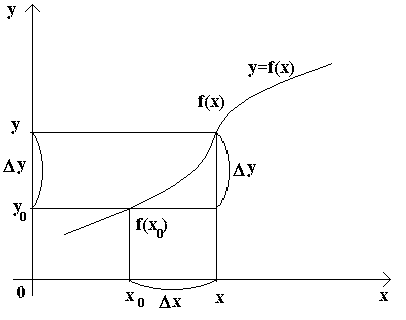
Давайте рассмотрим, что же такое приращение аргумента и функции на графике.

Рассмотрим ещё один пример.

Давайте вспомним определение непрерывной функции, которое мы формулировали ранее.

Определение непрерывности функции в точке x = a выглядит так:

Определение непрерывности функции в точке можно записать так:

Когда мы вводили определение непрерывной функции, то мы говорили, что функция непрерывна на промежутке X, если она непрерывна в каждой точке промежутка. Давайте уточним, что означает непрерывность функции в концевых точках промежутка, например, как понимать непрерывность функции в точках a и b отрезка [a; b].

Давайте изобразим график линейной функции. Отметим приращение аргумента и функции. И найдём чему равно отношение приращения аргумента к приращению функции.

Источник

Что значит приращение функции

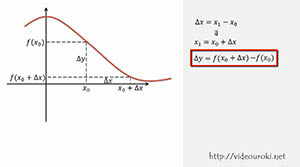
Определение : Пусть функция у = f(x) определена в точках х₀ и х₁. Разность х1 — х₀ называют приращением аргумента (при переходе от точки x₀ к x₁), а разность f(х₁) — f(x₀) называют приращением функции.

Приращение аргумента обозначают ΔX ( дельта икс, Δ — прописная буква греческого алфавита «дельта»; соответствующая строчная буква пишется так: δ). Приращение функции обозначают ΔY или Δ f.

Итак, x1 — x0 = Δ х, значит, х₁ = х0+ Δ x. f(x 1) — f(xо) = Δ у (или Δ f), значит,

Приращение функции в точке — функция обычно обозначаемая от новой переменной определяемая как

Переменная называется приращением аргумента.

В случае когда ясно о каком значении идёт речь, применяется более короткая запись.

Таким образом все эти непонятные иксы, игреки и дельты становятся вполне конкретными точками на плоскости. И мы понимаем,что фраза из определения приращения «Разность х1 — х₀ называют приращением аргумента (при переходе от точки x₀ к x₁), а разность f(х₁) — f(x₀) называют приращением функции» имеет вполне определенный смысл.

Надеюсь, что этот обзор помог вам разобраться с такими непонятными определениями, как приращение функции и приращение аргумента. Для тех же, кто по прежнему ничего не понял, я советую разобраться с такими базовыми понятиями, как функция и аргумент функции.

Источник

Решение производной для чайников: определение, как найти, примеры решений

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Решение:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Что значит приращение функции

рХУФШ ЙНЕЕН ОЕЛПФПТХА ЖХОЛГЙА y= f(x), ПРТЕДЕМЕООХА ОБ ОЕЛПФПТПН РТПНЕЦХФЛЕ. дМС ЛБЦДПЗП ЪОБЮЕОЙС БТЗХНЕОФБ x ЙЪ ЬФПЗП РТПНЕЦХФЛБ ЖХОЛГЙС y = f(x) ЙНЕЕФ ПРТЕДЕМЕООПЕ ЪОБЮЕОЙЕ.

уПУФБЧЙН ПФОПЫЕОЙЕ РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ

оБКДЕН РТЕДЕМ ЬФПЗП ПФОПЫЕОЙС РТЙ . еУМЙ ЬФПФ РТЕДЕМ УХЭЕУФЧХЕФ, ФП ЕЗП ОБЪЩЧБАФ РТПЙЪЧПДОПК ДБООПК ЖХОЛГЙЙ f(x) Ч ФПЮЛЕ x 0 Й ПВПЪОБЮБАФ f ‘( x 0 ). йФБЛ,

рТПЙЪЧПДОБС ПВПЪОБЮБЕФУС УЙНЧПМБНЙ f ‘ (x), y ‘, . лПОЛТЕФОПЕ ЪОБЮЕОЙЕ РТПЙЪЧПДОПК РТЙ x = a ПВПЪОБЮБЕФУС f ‘( a ) ЙМЙ .

пРЕТБГЙС ОБИПЦДЕОЙС РТПЙЪЧПДОПК ПФ ЖХОЛГЙЙ f(x) ОБЪЩЧБЕФУС ДЙЖЖЕТЕОГЙТПЧБОЙЕН ЬФПК ЖХОЛГЙЙ.

дМС ОЕРПУТЕДУФЧЕООПЗП ОБИПЦДЕОЙС РТПЙЪЧПДОПК РП ПРТЕДЕМЕОЙА НПЦОП РТЙНЕОЙФШ УМЕДХАЭЕЕ РТБЛФЙЮЕУЛПЕ РТБЧЙМП :

рТЙНЕТ 1

оБКФЙ РТПЙЪЧПДОХА ЖХОЛГЙЙ y = x 2

Б) Ч РТПЙЪЧПМШОПК ФПЮЛЕ;

a)

рТЙНЕТ 2

йУРПМШЪХС ПРТЕДЕМЕОЙЕ, ОБКФЙ РТПЙЪЧПДОХА ЖХОЛГЙЙ Ч РТПЙЪЧПМШОПК ФПЮЛЕ.

Источник

Что значит приращение функции

Приращение аргумента и функции

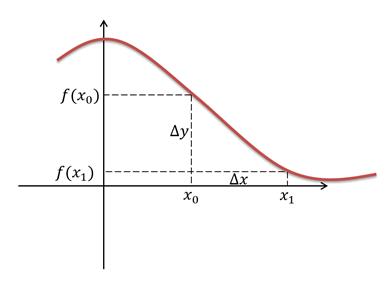
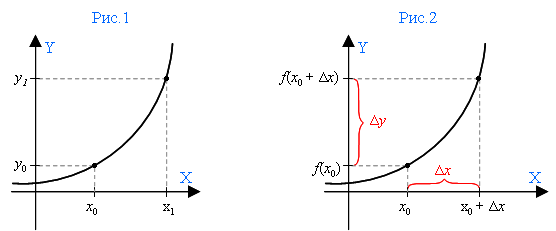
На оси Х – две точки: x₀ и x₁ (рис.1). Если от x₁ отнимем x₀, то узнаем длину шага между ними – а говоря иначе, узнаем, на сколько приросла точка x₀ в точке x₁. Эта разность между двумя заданными точками оси X и называется приращением аргумента.

Точки x₀ и x₁ образуют на оси Y соответственно точки у₀ и у₁. Если от у₁ отнять у₀, то мы получим приращение функции.

Итак, в функции y = f(x) относительно определенных точек x₀ и x₁:
разность x₁ – x₀ называется приращением аргумента, а разность у₁ – у₀ называется приращением функции.

Приращение обозначается греческой буквой Δ (дельта):

Можно сказать и иначе: если к x₀ прибавить величину приращения Δx, то мы получим точку x₁.
То есть x₁ = x₀ + Δx (рис.2).
Тогда точку f(x₁), отмеченную на первом рисунке как у₁, тоже можно обозначить иначе:
f(x₀ + Δx).

Осталось вывести формулу приращения функции.

Формула приращения функции:

Δy = f(x₀ + Δx) – f(x₀)

Δf = f(x₀ + Δx) – f(x₀)

Источник