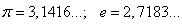Что значит ненатуральное число
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Математика
Тестирование онлайн
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3. и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом. Например:
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Округление чисел
Округлить 8,759123. с точностью до целой части.
Округлить 8,759123. с точностью до десятой части.
Округлить 8,759123. с точностью до сотой части.
Округлить 8,759123. с точностью до тысячной части.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это неправильные примеры натуральных чисел, потому что ноль расположен слева. По правилам так нельзя. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двухзначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа на него самого | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Числа. Натуральные числа.
Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Всякое натуральное число легко записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000. – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Обозначение натуральных чисел: Множество натуральных чисел обозначают символом N.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Сравнение натуральных чисел.
Таблица разрядов и классов чисел.
1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч
1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов
4-й класс миллиарды
1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы.
Основные свойства натуральных чисел.
Действия над натуральными числами.
1. Сложение натуральных чисел результат: сумма натуральных чисел.
Формулы для сложения:
В основном, сложение натуральных чисел выполняется « столбиком ».
2. Вычитание натуральных чисел – операция, обратная сложению: разница натуральных чисел.
Формулы для вычитания:
Вычитание натуральных чисел удобно производить « столбиком ».
3. Умножение натуральных чисел : произведение натуральных чисел.
Формулы для умножения:
(а + b) ∙ с= а ∙ с + b ∙ с
(а – b) ∙ с = а ∙ с – b ∙ с
4. Деление натуральных чисел – операция, обратная операции умножения.
Формулы для деления:
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо.
Когда в выражении есть скобки – сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.
Алгебра
План урока:
Натуральные числа
Ещё в далекие доисторические времена человек освоил такую математическую операцию, как счет. Можно было подсчитать количество соплеменников в племени или животных в стае, на которых велась охота. При этом человек ещё не осознавал понятие числа как некое отвлеченное понятие. Анализ языков народов, находящихся на самых низких стадиях развития, показывает, что они в словосочетаниях «три змеи», «три палки», «три камня» используют разные слова для числа 3. Однако со временем человек осознал, что количество предметов можно определять числом, которое не будет зависеть от природы подсчитываемых объектов. Числа, используемые для счета, сегодня называют натуральными числами. Долгое время человечество не знало никаких других чисел.
В качестве примера можно привести следующие натуральные числа: 1, 8, 10, 1000, 64141 и т.п. Если можно представить, что в каком-то множестве содержится N элементов, то N будет натуральным числом.
Вообще все натуральные числа являются частью так называемого натурального ряда чисел. Начинается этот ряд с единицы, а каждое следующее число больше предыдущего на 1.
Таким образом, можно дать ещё одно определение натуральных чисел – это числа, входящие в натуральный ряд. Традиционно ноль не является натуральным числом, ведь при подсчете предметов счет начинают с единицы. Такой подход используется в большинстве российских источников. Однако стоит отметить, что иногда в зарубежной литературе всё же предпочитают начинать натуральный ряд не с единицы, а с нуля. В этом случае 0 становится натуральным числом. Это деление весьма условно. Для обозначения множества натуральных чисел используется буква N. Очевидно, что натуральных чисел существует бесконечно много, а потому не существует наибольшего натурального числа.
Любые два натуральных числа можно складывать друг с другом и перемножать, при этом в результате будет снова получаться натуральное число. При вычитании может получиться ноль или отрицательное число, а при делении – дробное.
Простые и составные числа
Все натуральные числа можно разбить на три группы:
Единицу традиционно не считают ни простым, ни составным числом. Составным же называют натуральное число, делящееся не только на единицу и себя. Можно дать и другие определения, основанные на количестве делителей у числа. Так, единица имеет ровно 1 делитель. У простого числа всегда ровно 2 делителя, а у составного – 3 и более.
В качестве примера простых чисел можно привести: 2, 3, 5, 7, 31, 101, 163. Примерами составных чисел являются:
Среди делителей составного числа могут быть как другие составные, так и простые числа. Например, 50 имеет простые делители 2 и 5 и составные 10 и 25.
Заметим, что если число n делится на m, а m в свою очередь делится на k, то и n делится на k. Так, 45 делится на 9, а 9 делится на 3. Значит, и 45 делится на 3. Из этого свойства чисел вытекает следующее утверждение:
Любое составное число имеет хотя бы один простой делитель, причем им обязательно будет наименьший из всех делителей числа. Докажем это. Пусть число H – составное, и имеет наименьший делитель F. Предположим, что F – составное число. Тогда у него есть делитель L, который меньше его. Но тогда L должен быть делителем и для H. Так как L 1 1