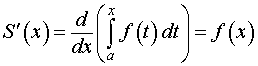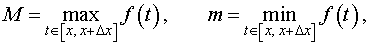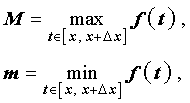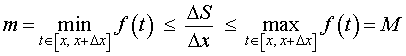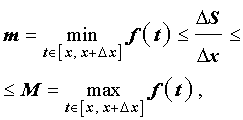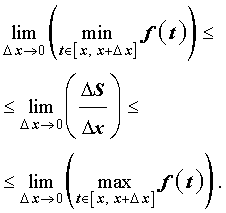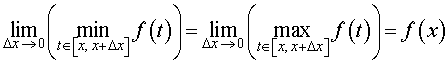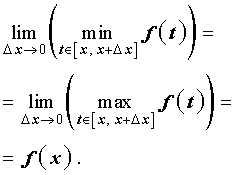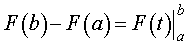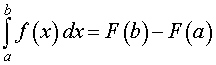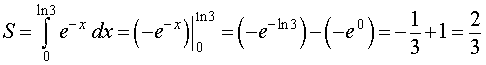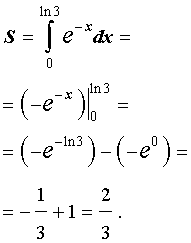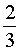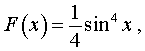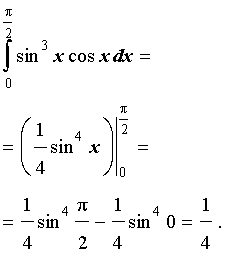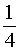Что выражает формула ньютона лейбница
Определенный интеграл как площадь криволинейной трапеции
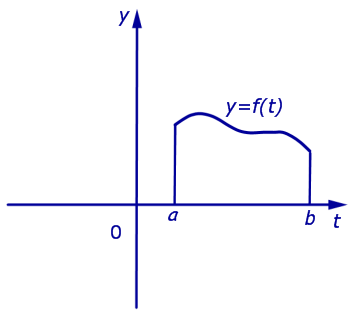
Пусть y = f (t) – непрерывная на отрезке [a, b] функция, принимающая только положительные значения.
Определение 1. Фигуру, ограниченную графиком функции y = f (t) сверху, отрезком [a, b] снизу, а справа и слева отрезками прямых t = a и t = b (рис. 2), называют криволинейной трапецией.
Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции f (t) в пределах от a до b и обозначают
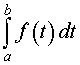 | (1) |
Формула (1) читается так: «Интеграл от a до b от функции f (t) по dt »
Определение 3. В формуле (1) функцию f (t) называют подынтегральной функцией, переменную t называют переменной интегрирования, отрезок [a, b] называют отрезком интегрирования, число b называют верхним пределом интегрирования, а число a – нижним пределом интегрирования.
Производная от определенного интеграла по верхнему пределу
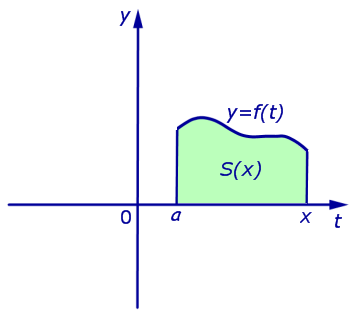
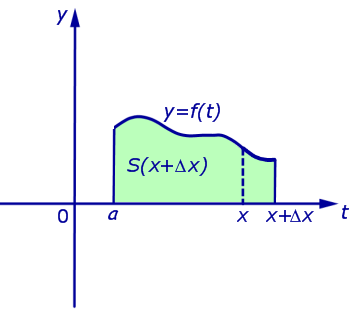
Если обозначить S (x) площадь криволинейной трапеции, ограниченной с боков отрезками прямых t = a и t = x (рис. 3),
то будет справедлива формула
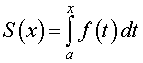 | (2) |
Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.
Другими словами, справедлива формула
Доказательство. Из формулы (2) следует, что
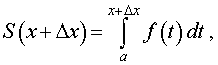 | (3) |
где через Δx обозначено приращение аргумента x (рис. 4)
Из формул (3) и (2) получаем, что
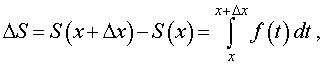 | (4) |
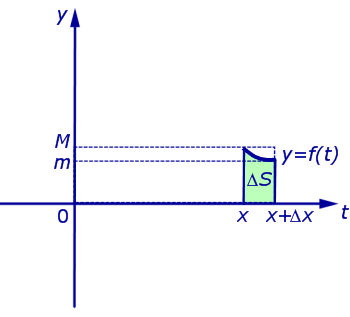
где через ΔS обозначено приращение функции S (x), соответствующее приращению аргумента Δx (рис. 5)
Если ввести обозначения
(см. раздел «Наибольшее и наименьшее значение функции на отрезке»), то можно заметить, что выполнено неравенство
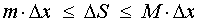 | (5) |
смысл которого заключается в том, что площадь криволинейной трапеции, изображенной на рисунке 5, не может быть меньше, чем площадь прямоугольника с основанием Δx и высотой m, и не может быть больше, чем площадь прямоугольника с основанием Δx и высотой M.
Из неравенства (5) следует, что
В силу непрерывности функции y = f (t) выполнено равенство
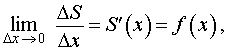 | (6) |
что и завершает доказательство теоремы 1.
Теорема Ньютона-Лейбница. Если F (x) – любая первообразная функции f (x), то справедливо равенство
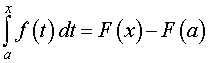 | (7) |
Воспользовавшись равенством (8), из формулы (2) получаем, что
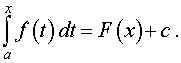 | (9) |
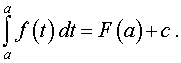 | (10) |
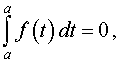 | (11) |
Из формул (10) и (11) следует, что
и формула (9) принимает вид
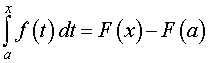
что и завершает доказательство теоремы Ньютона-Лейбница.
Замечание 1. Формулу (7) часто записывают в виде
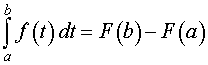 | (12) |
и называют формулой Ньютона-Лейбница.
Замечание 2. Для правой части формулы Ньютона-Лейбница часто используют обозначение
Замечание 4. Все определения и теоремы остаются справедливыми не только в случае положительных непрерывных функций f (x), но и для гораздо более широкого класса функций, имеющих произвольные знаки и интегрируемых по Риману, однако этот материал уже выходит за рамки школьного курса математики.
Примеры решения задач
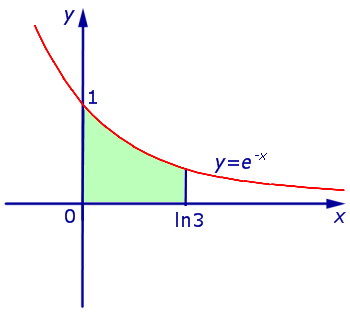
Задача 1. Найти площадь фигуры, ограниченной линиями
Решение. Рассматриваемая фигура является криволинейной трапеции (рис. 6)
Ответ.
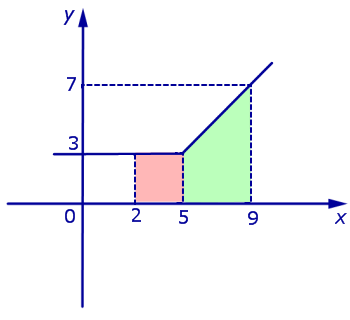
Задача 2. График функции y = f (x) изображен на рисунке 7.
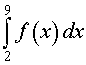 | (13) |
Решение. Интеграл (13) равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f (x), ограниченной снизу осью абсцисс Ox и ограниченной с боков отрезками прямых x = 2 и x = 9. Криволинейная трапеция состоит из квадрата, раскрашенного на рисунке 7 розовым цветом, и трапеции, раскрашенной на рисунке 7 зеленым цветом. Площадь квадрата равна 9, а площадь трапеции равна 20. Таким образом, интеграл (13) равен 29.
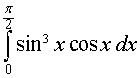 | (14) |
Решение. Поскольку одной из первообразных подынтегральной функции интеграла (14) является функция
то в соответствии с формулой Ньютона-Лейбница получаем
Ответ.
Вычисление определенного интеграла. Формула Ньютона-Лейбница
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Формула Ньютона-Лейбница
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Произведем вычисление F ( a ) с использованием первого свойства определенного интеграла. Тогда получаем, что
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Ответ: ∫ 1 3 x 2 d x = 26 3
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
Производим переход к вычислению второго интеграла.
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
Интегрирование по частям при вычислении определенного интеграла
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Формула Ньютона-Лейбница
Основная теорема анализа или формула Ньютона — Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной
Формулировка
Данный вид интеграла называется интегралом с переменным верхним пределом. Используя теорему о среднем в определённом интеграле, легко показать что данная функция непрерывная и дифференцируемая. А также производная от данной функции в точке x равна самой интегрируемой функции. От сюда следует, что любая непрерывная функция имеет первообразную в виде квадратуры: 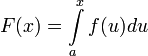
Смотреть что такое «Формула Ньютона-Лейбница» в других словарях:
Формула Ньютона — Лейбница — Основная теорема анализа или формула Ньютона Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной Формулировка Рассмотрим интеграл от функции y = f(x) в пределах от постоянного числа a до… … Википедия
НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА — основная формула интегрального исчисления. Выражает связь между определенным интегралом от функции f(x) и какой либо ее первообразной F(x) … Большой Энциклопедический словарь
Теорема Ньютона — Лейбница — Формула Ньютона Лейбница или теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то и … Википедия
Формула конечных приращений — У этого термина существуют и другие значения, см. Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия
Формула Стокса — Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2… … Википедия
Формула Лейбница — У этого термина существуют и другие значения, см. Список объектов, названных в честь Лейбница. У этого термина существуют и другие значения, см. Формула Лейбница (значения). Формулой Лейбница в интегральном исчислении называется правило… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Первообразная функции. Формула Ньютона-Лейбница
Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).
Сейчас объясним, что это значит.
Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.
Таблица первообразных
Первообразная суммы функций равна сумме их первообразных.
Первообразная разности функций — разности первообразных.
Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:
Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.
Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.
Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница)
Тогда площадь этой фигуры вычисляется по формуле:
Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».
Найдем первообразную функции с помощью таблицы первообразных. Получим:
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При x = 0 получим: Значит, и
По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.
Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть
Презентация на тему Формула Ньютона-Лейбница
Описание презентации по отдельным слайдам:
Описание слайда:
Работу выполнили:
Павшинцев И.С.
Чижков А.А.
Работу приняла:
Плешакова О.В.
2010 год
Описание слайда:
план
1-Ньютон и Лейбниц
2- теорема
3- интеграл
4- применение интеграла
5-историческое значение и философский смысл формулы
6- список используемой литературы интернет ресурсы
7- конец!
Описание слайда:
Описание слайда:
Ньютон и Лейбниц
Из сохранившихся документов историки науки выяснили, что дифференциальное и интегральное исчисление Ньютон открыл ещё в 1665-1666 годы, однако не публиковал его до 1704 года.[70] Лейбниц разработал свой вариант анализа независимо (с 1675 года), хотя первоначальный толчок, вероятно, его мысль получила из слухов о том, что такое исчисление у Ньютона уже имеется, а также благодаря научным беседам в Англии и переписке с Ньютоном. В отличие от Ньютона, Лейбниц сразу опубликовал свою версию, и в дальнейшем, вместе с Якобом и Иоганном Бернулли, широко пропагандировал это эпохальное открытие по всей Европе. Большинство учёных на континенте не сомневались, что анализ открыл Лейбниц.
Описание слайда:
Вняв уговорам друзей, взывавших к его патриотизму, Ньютон во 2-й книге своих «Начал» (1687) сообщил:[71]
В письмах, которыми около десяти лет тому назад я обменивался с весьма искусным математиком г-ном Лейбницем, я ему сообщал, что обладаю методом для определения максимумов и минимумов, проведения касательных и решения тому подобных вопросов, одинаково приложимых как для членов рациональных, так и для иррациональных, причем я метод скрыл, переставив буквы следующего предложения: «когда задано уравнение, содержащее любое число текущих количеств, найти флюксии[14] и обратно». Знаменитейший муж отвечал мне, что он также напал на такой метод и сообщил мне свой метод, который оказался едва отличающимся от моего, и то только терминами и начертанием формул.
Описание слайда:
В 1693 году, когда Ньютон наконец опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. Ньютон сообщил:[72]
Наш Валлис присоединил к своей «Алгебре», только что появившейся, некоторые из писем, которые я писал к тебе в своё время. При этом он потребовал от меня, чтобы я изложил открыто тот метод, который я в то время скрыл от тебя переставлением букв; я сделал это коротко, насколько мог. Надеюсь, что я при этом не написал ничего, что было 6ы тебе неприятно, если же это случилось, то прошу сообщить, потому что друзья мне дороже математических открытий.
Описание слайда:
После появления первой подробной публикации ньютонова анализа (математическое приложение к «Оптике», 1704) в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона. Рецензия ясно указывала, что автором нового исчисления является Лейбниц. Сам Лейбниц решительно отрицал, что рецензия составлена им, но историки сумели найти черновик, написанный его почерком.[70] Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего разгорелась общеевропейская приоритетная война, «наиболее постыдная склока во всей истории математики».[46]
Описание слайда:
31 января 1713 года Королевское общество получило письмо от Лейбница, содержащее примирительную формулировку: он согласен, что Ньютон пришёл к анализу самостоятельно, «на общих принципах, подобных нашим». Рассерженный Ньютон потребовал создать международную комиссию для прояснения приоритета. Комиссии не понадобилось много времени: спустя полтора месяца, изучив переписку Ньютона с Ольденбургом и другие документы, она единогласно признала приоритет Ньютона, причём в формулировке, на этот раз оскорбительной в отношении Лейбница. Решение комиссии было напечатано в трудах Общества с приложением всех подтверждающих документов
Описание слайда:
В ответ с лета 1713 года Европу наводнили анонимные брошюры, которые отстаивали приоритет Лейбница и утверждали, что «Ньютон присваивает себе честь, принадлежащую другому». Брошюры также обвиняли Ньютона в краже результатов Гука и Флемстида.[70] Друзья Ньютона, со своей стороны, обвинили в плагиате самого Лейбница; по их версии, во время пребывания в Лондоне (1676) Лейбниц в Королевском обществе ознакомился с неопубликованными работами и письмами Ньютона, после чего изложенные там идеи Лейбниц опубликовал и выдал за свои.[73]
Война не ослабевала до декабря 1716 года, когда аббат Конти сообщил Ньютону: «Лейбниц умер — диспут окончен
Описание слайда:
теорема
Теорема
Если f непрерывна на отрезке a,b и Ф — ее любая первообразная на этом отрезке, то имеет место равенство
Описание слайда:
Пусть на отрезке (a,b) задана интегрируемая функция ʄ Начнем с того, что отметим, что
то есть не имеет никакого значения, какая буква ( x или u ) стоит под знаком ʄ в определенном интеграле по отрезку (a,b)
Описание слайда:
Зададим произвольное значение x € (a.b) и определим новую функцию
Описание слайда:
Покажем, что F непрерывна на отрезке (a,b) В самом деле, пусть
тогда
Описание слайда:
Описание слайда:
Описание слайда:
Далее, в силу непрерывности ʄ в точке x для всякого ε ˃0 можно указать такое δ что
для
Поэтому
что доказывает, что левая часть этого неравенства есть о(1) при h→0
Описание слайда:
имеет производную, равную
Следовательно, функция F(x) есть первообразная для ʄ (a,b)
Описание слайда:
Где C — некоторая постоянная. Полагая в этом равенстве x=a и учитывая, что F(a)=0 получим
Ф(a)=C Таким образом, Но
Описание слайда:
Описание слайда:
Интеграл
Интеграл функции — естественный аналог суммы последовательности. Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию. Процесс нахождения интеграла называется интегрированием.
Существует несколько различных определений операции интегрирования, отличающиеся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат.
Описание слайда:
Типы интегралов
Определённый интеграл
Неопределённый интеграл
Интеграл Римана и Римана — Стилтьеса
Интеграл Лебега и Лебега — Стилтьеса
Интеграл Даниэля
Кратный интеграл
Криволинейный интеграл
Поверхностный интеграл
Эллиптический интеграл
Описание слайда:
История
Знаки интеграла ʃ дифференцирования dx были впервые использованы Лейбницем в конце XVII века. Символ интеграла образовался из буквы S — сокращения слова лат. summa (сумма).
Интеграл в древности
Интегрирование прослеживается ещё в древнем Египте, примерно в 1800 до н. э., Московский математический папирус демонстрирует знание формулы объёма усечённой пирамиды. Первым известным методом для расчёта интегралов является метод исчерпывания Евдокса (примерно 370 до н. э.), который пытался найти площади и объёмы, разрывая их на бесконечное множество частей, для которых площадь или объём уже известны. Этот метод был подхвачен и развит Архимедом, и использовался для расчёта площадей парабол и приближенного расчёта площади круга. Аналогичные методы были разработаны независимо в Китае в 3-м веке н.э Лю Хуэйем, который использовал их для нахождения площади круга. Этот метод был впоследствии использован Дзю Чонгши для нахождения объёма шара.
Описание слайда:
Историческое значение и философский смысл
формулы Ньютона-Лейбница
Одним из важнейших исследовательских инструментов этого ряда является формула Ньютона-Лейбница, и стоящий за ней метод нахождения первообразной функции путем интегрирования ее производной. Историческое значение формулы в использовании бесконечно малых величин и абсолютно точном ответе на поставленный вопрос. Общеизвестны преимущества применения этого метода для решения математических, физических и прочих естественнонаучных задач, например, классической задачи о квадратуре круга – построении квадрата равновеликого заданному кругу. Философский смысл – в возможности получения информации о целом по его бесконечно малой части, замеченный ранее – наглядно реализуется в медицине и биологии, примером чему могут служить успехи генной инженерии в клонировании – создании взаимоподобных живых существ. Редким исключением в перечне наук, воспользовавшихся формулой Ньютона-Лейбница, остается история. Невозможность представления информации исторических источников в виде цифр – аргументов формулы – традиционна. Таким образом, до сих пор философский смысл формулы является не совсем философским, так как реализуется лишь в естественнонаучном знании, оставляя социально-гуманитарное знание без столь мощного инструмента. Хотя, если придерживаться традиционных особенностей социально-гуманитарного знания, его так сказать, слабостей, то и по делом ему.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
1. Бродский И.А. Сочинения в четырех томах. Т.3. СПб., 1994.
2. Вернадский В.И. Биосфера и ноосфера. М., 2003.
3. Вундт, Вильгельм. Введение в философию. М., 2001.
4. Гайденко П.П. Эволюция понятия науки. М., 1980.
5. Декарт, Рене. Размышления о первоначальной философии. СПб., 1995.
6. Карпов Г.М. Великое посольство Петра I. Калининград, 1998.
7. Кунцман П., Буркард Ф.-П., Видман Ф. Философия: dtv-Atlas. М., 2002.
8. Малаховский В.С. Избранные главы истории математики. Калининград, 2002.
9. Натансон И.П. Краткий курс высшей математики. СПб., 2001.
10. Энгельс Ф. Анти-Дюринг. М., 1988.
11. Шереметевский В.П. Очерки по истории математики. М., 2004
Интернет ресурсы
http://ru.wikipedia.org
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.