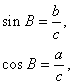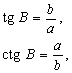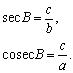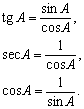Тригонометрия что это такое простыми словами

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

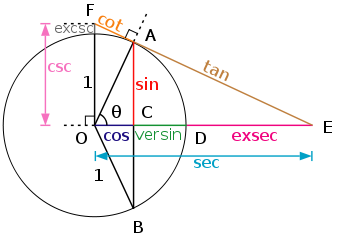
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

Тригонометрия

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

В Школе СССР имела статус учебного предмета.

Содержание

Определение тригонометрических функций

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

История

Древняя Греция

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β Средневековая Индия

Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

Индийцы также знали формулы для кратных углов , , где .

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.

Источник

ТРИГОНОМЕТРИЯ

ТРИГОНОМЕТРИЯ – (от греч. trigwnon – треугольник и metrew – измеряю) – математическая дисциплина, изучающая зависимости между углами и сторонами треугольников и тригонометрические функции.

Термин «тригонометрия» ввел в употребление в 1595 немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. К концу 16 в. большинство тригонометрических функций было уже известно, хотя само это понятия еще не существовало.

В тригонометрии выделяют три вида соотношений: 1) между самими тригонометрическими функциями; 2) между элементами плоского треугольника (тригонометрия на плоскости); 3) между элементами сферического треугольника, т.е. фигуры, высекаемой на сфере тремя плоскостями, проходящими через ее центр. Тригонометрия началась именно с наиболее сложной, сферической части. Она возникла прежде всего из практических нужд. Древние наблюдали за движением небесных светил. Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Наблюдения за звездным небом с незапамятных времен вели и астрологи.

Естественно, все измерения, связанные с расположением светил на небосводе, – измерения косвенные. Прямые могли быть проведены только на поверхности Земли, но и здесь далеко не всегда удавалось непосредственно определить расстояние между какими-то пунктами и тогда вновь прибегали к косвенным измерениям. Например, вычисляли высоту дерева, сравнивая длину его тени с длиной тени от какого-нибудь шеста, высота которого была известна. Аналогичным образом вычисляли и размеры острова в море. Подобные задачи сводятся к анализу треугольника, в котором одни его элементы выражают через другие. Этим и занимается тригонометрия. А поскольку звезды и планеты представлялись древним точками на небесной сфере, то сначала стала развиваться именно сферическая тригонометрия. Ее считали разделом астрономии.

А начиналось все очень давно. Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. Астрономы Междуречья научились предсказывать положение Земли и Солнца и именно от них к нам пришла система измерения углов в градусах, минутах и секундах, потому что у вавилонян была принята шестидесятеричная система счисления.

Однако первые по-настоящему важные достижения принадлежат древнегреческим ученым. Например, 12-я и 13-я теоремы второй книги Начал Евклида (конец 4–3 в. до н. э.) выражают по существу теорему косинусов. Во 2 в. до н.э. астроном Гиппарх из Никеи (180–125 до н.э.) составил таблицу для определения соотношений между элементами треугольников. Такие таблицы нужны потому, что значения тригонометрических функций нельзя вычислить по аргументам с помощью арифметических операций. Тригонометрические функции приходилось рассчитывать заранее и хранить в виде таблиц. Гиппарх подсчитал в круге заданного радиуса длины хорд, отвечающих всем углам от 0 до 180°, кратным 7,5°. По существу, это таблица синусов. Труды Гиппарха до нас не дошли, но многие сведения из них включены в Альмагест (II в.) – знаменитое сочинение в 13 книгах греческого астронома и математика Клавдия Птолемея (ум. ок.160 н. э.). Древние греки не знали синусов, косинусов и тангенсов, вместо таблиц этих величин они употребляли таблицы, позволявшие находить хорду окружности по стягиваемой дуге. В Альмагесте автор приводит таблицу длин хорд окружности радиуса в 60 единиц, вычисленных с шагом 0,5° с точностью до 1/3600 единицы, и объясняет, как эта таблица составлялась. Труд Птолемея несколько веков служил введением в тригонометрию для астрономов.

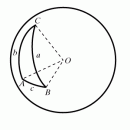
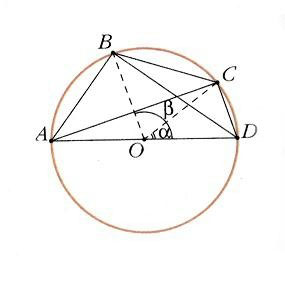
Чтобы понять, как ученые древности составляли тригонометрические таблицы, надо познакомиться с методом Птолемея. Метод основан на теореме – произведение диагоналей вписанного в окружность четырехугольника равно сумме произведений его противоположных сторон.

Пусть ABCD – вписанный четырехугольник, АD – диаметр окружности, а точка O – ее центр (рис. 1). Если известно, как вычислять хорды, стягивающие углы DOC = a и DОВ = b, т. е. сторону СD и диагональ B, то, по теореме Пифагора, из прямоугольных треугольников АDВ и АDС можно найти АВ и АС, а потом, по теореме Птолемея, – BC = (АС·ВD – АВ·СD) /АD, т.е. хорду, стягивающую угол ВОС = b – a. Некоторые хорды, например стороны квадрата, правильных шестиугольника и восьмиугольника, отвечающие углам 90, 60 и 45°, легко определить. Известна также сторона правильного пятиугольника, которая стягивает дугу в 72°. Приведенное выше правило позволяет вычислять хорды для разностей этих углов, например для 12° = 72° – 60°. Кроме того, можно находить хорды половинных углов, однако этого недостаточно, чтобы рассчитать, чему равна хорда дуги в 1°, – хотя бы потому, что все названные углы кратны 3°. Для хорды 1° Птолемей нашел оценку, показав, что она больше 2/3 хорды (3/2)° и меньше 4/3 хорды (3/4)° – двух чисел, совпадающих с достаточной для его таблиц точностью.

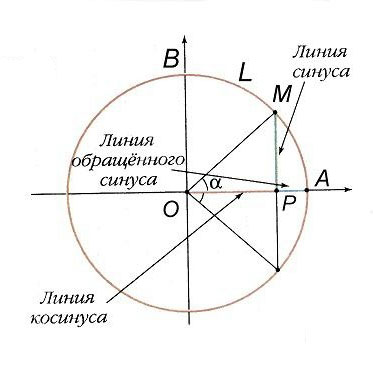
Если греки по углам вычисляли хорды, то индийские астрономы в сочинениях 4–5 вв. перешли к полухордам двойной дуги, т.е. в точности к линиям синуса (рис. 2). Они пользовались и линиями косинуса – вернее, не его самого, а «обращенного» синуса, получившего позднее в Европе название «синус-верзус», сейчас эта функция, равная 1 – cos a, уже не употребляется. Впоследствии тот же подход привел к определению тригонометрических функций через отношения сторон прямоугольного треугольника.

За единицу измерения отрезков MP, OP, PA принималась дуговая минута. Так, линия синуса дуги AB = 90° есть OB – радиус окружности; дуга AL, равная радиусу, содержит (округленно) 57°18′ = 3438′.

Дошедшие до нас индийские таблицы синусов (древнейшая составлена в 4–5 веке н.э.) не столь точны, как птолемеевы; они составлены через 3°45′ (т.е. через 1/24 часть дуги квадранта).

Термины «синус» и «косинус» пришли от индийцев, не обошлось и без любопытного недоразумения. Полухорду индийцы называли «ардхаджива» (в переводе с санскрита – «половина тетивы лука»), а потом сократили это слово до «джива». Мусульманские астрономы и математики, получившие знания по тригонометрии от индийцев, восприняли его как «джиба», а затем оно превратилось в «джайб», что на арабском языке означает «выпуклость», «пазуха». Наконец, в 7 в. «джайб» буквально перевели на латынь словом «sinus», которое не имело никакого отношения к обозначаемому им понятию. Санскритское «котиджива» – синус остатка (до 90°), а на латинском – sinus complementi, т.е. синус дополнения, в 17 в. сократилось до слова «косинус». Наименования «тангенс» и «секанс» (в переводе с латинского означающие «касательная» и «секущая») введены в 1583 немецким ученым Финком.

Большой вклад в развитие тригонометрии внесли арабские ученые, например, Аль-Баттани (ок. 900 н.э.). В 10 в. багдадский ученый Мухаммед из Буджана, известный под именем Абу-ль-Вефа (940–997), присоединил к линиям синусов и косинусов линии тангенсов, котангенсов, секансов и косекансов. Он дает им те же определения, которые содержатся и в наших учебниках. Абу-ль-Вефа устанавливает и основные соотношения между этими линиями.

Итак, к концу 10 в. ученые исламского мира уже оперировали, наряду с синусом и косинусом, четырьмя другими функциями – тангенсом, котангенсом, секансом и косекансом; открыли и доказали несколько важных теорем плоской и сферической тригонометрии; использовали окружность единичного радиуса (что позволило толковать тригонометрические функции в современном смысле); придумали полярный треугольник сферического треугольника. Арабские математики составили точные таблицы, например таблицы синусов и тангенсов с шагом в 1′ и точностью до 1/700 000 000. Очень важной прикладной задачей была и такая: научиться определять направление на Мекку для пяти ежедневных молитв, где бы ни находился мусульманин.

Особенно большое влияние на развитие тригонометрии оказал Трактат о полном четырехстороннике астронома Насир-эд-Дин из Туса (1201–1274), известного так же под именем ат-Туси. Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная область математики.

В 12 в. был переведен с арабского языка на латинский ряд астрономических работ, по ним впервые европейцы познакомились с тригонометрией.

Трактат Насир-эд-Дина произвел большое впечатление на немецкого астронома и математика Иоганна Мюллера (1436–1476). Современники больше знали его под именем Региомонтана (так переводится на латинский название его родного города Кенигсберга, ныне – Калининграда). Региомонтан составил обширные таблицы синусов (через 1 минуту с точностью до седьмой значащей цифры). Он впервые отступил от шестидесятиричного деления радиуса и за единицу измерения линии синуса принял одну десятимиллионную часть радиуса. Таким образом, синусы выражались целыми числами, а не шестидесятиричными дробями. До введения десятичных дробей оставался только один шаг, но он потребовал более 100 лет. Труд Региомонтана О треугольниках всех родов пять книг сыграл в европейской математике ту же роль, что и сочинение Насир-эд-Дина в науке мусульманских стран.

За таблицами Региомонтана последовал ряд других, еще более подробных. Друг Коперника Ретик (1514–1576) вместе с несколькими помощниками в течение 30 лет работал над таблицами, законченными и изданными в1596 его учеником Отто. Углы шли через 10», а радиус делился на 1 000 000 000 000 000 частей, так что синусы имели 15 верных цифр.

Дальнейшее развитие тригонометрии шло по пути накопления и систематизации формул, уточнения основных понятий, становления терминологии и обозначений. Многие европейские математики работали в области тригонометрии. Среди них такие великие ученые, как Николай Коперник (1473–1543), Тихо Браге (1546–1601) и Иоганн Кеплер (1571–1630). Франсуа Виет (1540–1603) дополнил и систематизировал различные случаи решения плоских и сферических треугольников, открыл «плоскую» теорему косинусов и формулы для тригонометрических функций от кратных углов. Исаак Ньютон (1643–1727) разложил эти функции в ряды и открыл путь для их использования в математическом анализе. Леонард Эйлер (1707–1783) ввел и само понятие функции, и принятую в наши дни символику. Величины sin x, cos x и т.д. он рассматривал как функции числа x – радианной меры соответствующего угла. Эйлер давал числу x всевозможные значения: положительные, отрицательные и даже комплексные. Он также обнаружил связь между тригонометрическими функциями и экспонентой комплексного аргумента, что позволило превратить многочисленные и зачастую весьма замысловатые тригонометрические формулы в простые следствия из правил сложения и умножения комплексных чисел. Он же ввел и обратные тригонометрические функции.

К концу 18 в. тригонометрия как наука уже сложилась. Тригонометрические функции нашли применение в математическом анализе, физике, химии, технике – везде, где приходится иметь дело с периодическими процессами и колебаниями – будь то акустика, оптика или качание маятника.

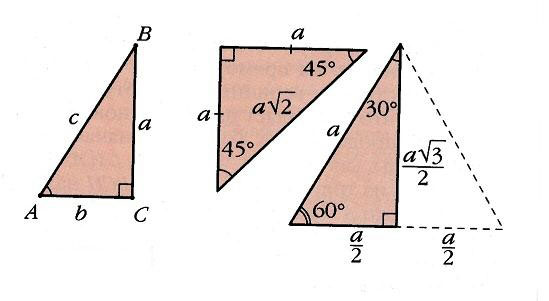
Решение любых треугольников, в конечном счете, сводится к решению прямоугольных треугольников (т.е. таких, у которых один из углов – прямой). Поскольку все прямоугольные треугольники с заданным острым углом подобны друг другу, отношения их соответственных сторон одинаковы. Например, в прямоугольном треугольнике ABC отношение двух его сторон, например, катета а к гипотенузе с, зависит от величины одного из острых углов, например А. Отношения различных пар сторон прямоугольного треугольника и называются тригонометрическими функциями его острого угла. Всего таких отношений в треугольнике шесть, и им отвечают шесть тригонометрических функций (обозначения сторон и углов треугольника на рис. 3).

Синус 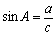(отношение противолежащего катета к гипотенузе),

косинус 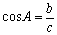(отношение прилежащего катета к гипотенузе),

тангенс 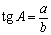(отношение противолежащего катета к прилежащему),

котангенс 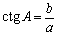(отношение прилежащего катета к противолежащему),

секанс sec A = 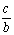(отношение гипотенузы к прилежащему катету),

косеканс cosec A = 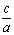(отношение гипотенузы к противолежащему катету).

По отношению к углу B («дополнительному» углу по отношению к А) формулы меняются соответственно:

Из определений вытекает несколько равенств, связывающих тригонометрические функции одного и того же угла между собой:

С учетом теоремы Пифагора a 2 + b 2 = c 2 можно выразить все шесть функций через какую-нибудь одну. Например, синус и косинус связаны основным тригонометрическим тождеством

Некоторые соотношения между функциями:

Эти формулы справедливы и для тригонометрических функций любого угла, но ими надо пользоваться осторожно, поскольку правые и левые части могут иметь разные области определения.

Есть только два прямоугольных треугольника, у которых и углы «хорошие» (выражаются целым или рациональным числом градусов), и хотя бы одно из отношений сторон рационально. Это равнобедренный треугольник (с углами 45, 45 и 90°) и половина равностороннего треугольника (с углами 30, 60, 90°) – как раз те два случая, когда значения тригонометрических функций удается вычислить прямо по определению. Эти значения приведены в таблице

Источник

Тригонометрия – это просто и понятно

Презентация к уроку

Подходя к школе, слышу голоса ребят из спортивного зала, иду дальше – поют, рисуют… везде эмоции, чувства. Мой кабинет, урок алгебры, десятиклассники. Вот и наш учебник, в котором курс тригонометрии составляет половину его объема, и в нем две закладки – это те места, где я нашла слова, не относящиеся к теории тригонометрии.

К числу немногих относятся учащиеся, которые любят математику, чувствует ее красоту и не спрашивает, зачем нужно изучать тригонометрию, где применяется изученный материал? Большинство – кто просто выполняет задания, чтобы не получить плохую оценку. И твердо уверены в том, что прикладное значение математики – это получить знания, достаточные для успешной сдачи ЕГЭ и поступления в ВУЗ (поступить и забыть).

Основная цель представляемого урока – показать прикладное значение тригонометрии в различных сферах деятельности человека. Приведенные примеры помогут учащимся увидеть связь этого раздела математики с другими предметами, изучаемыми в школе. Содержание этого урока – элемент профессиональной подготовки учащихся.

Рассказать новое о, казалось бы, давно известном факте. Показать логическую связь между тем, что уже знаем, и то, что предстоит изучить. Немного приоткрыть дверь и заглянуть за рамки школьной программы. Необычные задачи, связь с событиями сегодняшнего дня – вот те приемы, которые я использую для достижения поставленных целей. Ведь школьная математика как предмет способствует не столько обучению, сколько развитию личности, его мышления, культуры.

2. Конспект урока по алгебре и началам анализа (10 класс).

Организационный момент: Расставить шесть столов полукругом (модель транспортира), листы с заданиями для учащихся на столах (Приложение 1).

Объявление темы урока: “Тригонометрия – это просто и понятно”.

В курсе алгебры и начал анализа мы приступаем к изучению тригонометрии, мне хотелось бы рассказать о прикладном значении этого раздела математики.

“Великая книга природы может быть прочтена только теми, кто знает язык, на котором она написана, и этот язык – математика”.
(Г. Галилей).

В конце урока подумаем вместе, смогли ли мы заглянуть в эту книгу и понять язык, на котором она написана.

Тригонометрия – слово греческое и в переводе означает “измерение треугольников”. Возникновение тригонометрии связано с измерениями на земле, строительным делом, астрономией. А первое знакомство с ней произошло тогда, когда вы взяли в руки транспортир. Обратили вы внимание на то, как стоят столы? Прикиньте в уме: если принять один стол за хорду, то какова градусная мера дуги, которую она стягивает?

Вспомним о мере измерения углов: 1 ° = 1/ 360 часть окружности (“градус” – от латинского grad – шаг). Знаете ли вы, почему окружность разделили на 360 частей, почему не разбили на 10, 100 или 1000 частей, как это происходит, например, при измерении длин? Расскажу вам одну из версий.

Раньше люди считали, что Земля – это центр Вселенной и она неподвижна, а Солнце совершает за сутки один оборот вокруг Земли, геоцентрическая система мира, “гео” – Земля (Рисунок № 1). Вавилонские жрецы, проводившие астрономические наблюдения, обнаружили, что в день равноденствия Солнце от восхода до заката описывает на небесном своде полуокружность, в которой видимый поперечник (диаметр) Солнца укладывается ровно 180 раз, 1 ° – след Солнца. (Рисунок № 2).

Долгое время тригонометрия носила чисто геометрический характер. В вы продолжаете знакомство с тригонометрией, решая прямоугольные треугольники. Узнаёте, что синус острого угла прямоугольного треугольника – это есть отношение противолежащего катета к гипотенузе, косинус – отношение прилежащего катета к гипотенузе, тангенс – отношение противолежащего катета к прилежащему катету и котангенс – отношение прилежащего катета к противолежащему. И запоминаете, что в прямоугольном треугольнике, имеющем данный угол, отношения сторон не зависят от размеров треугольника. Знакомитесь с теоремами синусов и косинусов для решения произвольных треугольников.

В 2010 году московскому метрополитену исполнилось 75 лет. Каждый день мы спускаемся в метро и не замечаем, что …

Задача № 1. Угол наклона всех эскалаторов московского метро равен 30 градусам. Зная это, количество ламп на эскалаторе и примерное расстояние между лампами, можно вычислить примерную глубину заложения станции. На эскалаторе станции “Цветной бульвар” 15 ламп, а на станции “Пражская” 2 лампы. Рассчитайте, какова глубина заложения этих станций, если расстояния между лампами, от входа эскалатора до первой лампы и от последней лампы до выхода с эскалатора равны 6 м (Рисунок № 3). Ответ: 48 м и 9 м

Домашнее задание. Самая глубокая станция московского метро – “Парк Победы”. Какова глубина её заложения? Предлагаю вам самостоятельно найти недостающие данные для решения домашней задачи.

У меня в руках лазерная указка, она же – дальномер. Измерим, например, расстояние до доски.

Китайский дизайнер Хуань Цяокун догадался соединить в одно устройство два лазерных дальномера, транспортир и получил инструмент, позволяющий определять расстояние между двумя точками на плоскости (Рисунок № 4). Как вы думаете, с помощью какой теоремы решается эта задача? Вспомните формулировку теоремы косинусов. Согласны ли вы со мной, что ваших знаний уже достаточно для того, чтобы сделать такое изобретение? Решайте задачи по геометрии и совершайте каждый день маленькие открытия!

Помимо плоской геометрии Евклида (планиметрии) могут существовать и другие геометрии, в которых рассматриваются свойства фигур не на плоскости, а на других поверхностях, например на поверхности шара (Рисунок № 5). Первый математик, заложивший фундамент для развития неевклидовых геометрий был Н.И. Лобачевский – “Коперник геометрии”. С 1827 г. в течение 19 лет он был ректором Казанский Университета.

Сферическая тригонометрия, являющаяся частью сферической геометрии, рассматривает соотношения между сторонами и углами треугольников на сфере, образованных дугами больших кругов на сфере (Рисунок № 6).

Исторически сферическая тригонометрия и геометрия возникли из потребностей астрономии, геодезии, навигации, картографии. Подумайте, какое из этих направлений в последние годы получило столь бурное развитие, что его результат уже применяется в современных коммуникаторах. … Современное применение навигации – это система спутниковой навигации, которая позволяет определить местоположение и скорость объекта по сигналу его приемника.

Глобальная Навигационная Система (GPS). Для определения широты и долготы приемника необходимо, как минимум, принимать сигналы от трех спутников. Прием сигнала от четвертого спутника позволяет определить и высоту объекта над поверхностью (Рисунок № 7).

Компьютер приемника решает четыре уравнения с четырьмя неизвестными до тех пор, пока не найдется решение, которое проводит все окружности через одну точку (Рисунок № 8).

Знания из тригонометрии острого угла оказались недостаточны для решения более сложных практических задач. При изучении вращательных и круговых движений значение величины угла и круговой дуги не ограничены. Возникла необходимость перехода к тригонометрии обобщенного аргумента.

В качестве модели, с помощью которой математики работают с углами, была выбрана окружность (Рисунок № 9). Положительные углы откладываются против часовой стрелки, отрицательные – по часовой. Знакомы ли вы с историей такого соглашения?

Как известно, механические и солнечные часы устроены так, что их стрелки вращаются “по солнцу”, т.е. в том же направлении, в каком мы видим кажущееся нам движение Солнца вокруг Земли. (Вспомните начало урока – геоцентрическая система мира). Но с открытием Коперником истинного (положительного) движения Земли вокруг Солнца, видимое нами (т.е. кажущееся) движение Солнца вокруг Земли является фиктивным (отрицательным). Гелиоцентрическая система мира (гелио – Солнце) (Рисунок № 10).

В 2010 прошли Зимние Олимпийские игры в Ванкувере, критерии выставления оценок за выполненное упражнение фигуристом мы узнаем, решив задачу.

Задача № 2. Если фигурист совершает поворот на угол 10 800 градусов при выполнении упражнения “винт” за 12 секунд, то он получает оценку “отлично”. Определите, какое количество оборотов совершит фигурист за это время и скорость его вращения (обороты в секунду). Ответ: 2,5 оборота/сек.

Домашнее задание. На какой угол поворачивается фигурист, получивший оценку “неудовлетворительно”, если при таком же времени вращения его скорость была 2 оборота в секунду.

Наиболее удобной мерой измерения дуг и углов, связанных с вращательными движениями, оказалась радианная (радиусная) мера, как более крупная единица измерения угла или дуги (Рисунок № 11). Эта мера измерения углов вошла в науку через замечательные труды Леонарда Эйлера. Швейцарец по происхождению, он 30 лет прожил в России, был членом Петербургской Академии наук. Именно ему мы обязаны “аналитической” трактовкой всей тригонометрии, он вывел формулы, которые вы сейчас изучаете, ввел единообразные знаки:. sin x, cos x, tg x, ctg x.

Если до 17-го века развитие учения о тригонометрических функциях строилось на геометрической основе, то, начиная с 17-го века, тригонометрические функции начали применять к решению задач механики, оптики, электричества, для описания колебательных процессов, распространения волн. Везде, где приходится иметь дело с периодическими процессами и колебаниями, нашли применение тригонометрические функции. Функции, выражающие законы периодических процессов, обладают особым только им присущим свойством: они повторяют свои значения через один и тот же промежуток изменения аргумента. Изменения всякой функции наиболее наглядно передаются на её графике (Рисунок № 12).

Мы уже обращались за помощью к своему организму, при решении задач на вращение. Давайте прислушаемся к биению своего сердца. Сердце – самостоятельный орган. Головной мозг управляет любой нашей мышцей, кроме сердечной. У нее есть собственный центр управления – синусный узел. При каждом сокращении сердца по всему организму – начиная от синусного узла (размером с просяное зерно)– распространяется электрический ток. Его можно зарегистрировать с помощью электрокардиографа. Он вычерчивает электрокардиограмму (синусоиду) (Рисунок № 13).

Теперь поговорим о музыке. Математика – это музыка, это союз ума и красоты.
Музыка – это математика по вычислениям, алгебра по абстрагированию, тригонометрия по красоте. Гармоническое колебание (гармоника) – это синусоидальное колебание. График показывает, как изменяется воздушное давление на барабанную перепонку слушателя: вверх и вниз по дуге, периодически. Воздух давит то сильнее, то слабее. Сила воздействия совсем невелика и колебания происходят очень быстро: сотни и тысячи толчков каждую секунду. Такие периодические колебания мы воспринимаем как звук. Сложение двух различных гармоник дает колебание более сложной формы. Сумма трех гармоник – еще сложнее, а естественные, природные звуки и звуки музыкальных инструментов складываются из большого количества гармоник. (Рисунок № 14.)

Каждая гармоника характеризуется тремя параметрами: амплитудой, частотой и фазой. Частота колебаний показывает, сколько толчков давления воздуха происходит за одну секунду. Большие частоты воспринимаются как «высокие», «тонкие» звуки. Выше 10 КГц – писк, свист. Маленькие частоты воспринимаются как «низкие», «басовые» звуки, рокот. Амплитуда – это размах колебаний. Чем размах больше, тем сильнее воздействие на барабанную перепонку, и тем громче звук, который мы слышим (Рисунок № 15). Фаза – это смещение колебаний во времени. Фаза может измеряться в градусах или радианах. В зависимости от фазы смещается нулевой отсчет на графике. Для задания гармоники достаточно указать фазу от –180 до +180 градусов, поскольку при больших значениях колебание повторяется. Два синусоидальных сигнала с одинаковыми амплитудой и частотой, но разными фазами складываются алгебраически (Рисунок № 16).

Итог урока. Как вы думаете, смогли мы прочитать несколько страниц из Великой книги природы? Узнав о прикладном значении тригонометрии, стала ли вам более понятна ее роль в различных сферах деятельности человека, понятен ли вам был изложенный материал? Тогда вспомните и перечислите сферы применения тригонометрии, с которыми вы познакомились сегодня или знали ранее. Я надеюсь, что каждый из вас нашел в сегодняшнем уроке что-то новое для себя, интересное. Быть может, это новое подскажет вам путь в выборе будущей профессии, но, кем бы вы ни стали, ваша математическая образованность поможет стать профессионалом своего дела и интеллектуально развитым человеком.

Домашнее задание. Ознакомиться с конспектом урока (Приложение № 2), решить задачи (Приложение № 1).

Источник