Триада информатика что это
Перевод из одной системы счисления в другую с помощью триад и тетрад
Развивающая – развивать познавательный интерес учащихся, умения применять полученные знания на практике.
Воспитательная – повысить уровень информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения домашнего упражнения
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями двойки, то перевод чисел из этих СС в 2-ую и наоборот прост и основан на методах триад и тетрад. Число делится на триады (тетрады) вправо и влево от десятичной точки. Если крайние триады (тетрады) оказались неполными, они дополняются нулями.
| Алфавит | Триады | Тетрады |
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
Упражнение: Выполнить перевод, используя тетрады и триады:
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
Использование таблицы треад и тетрад
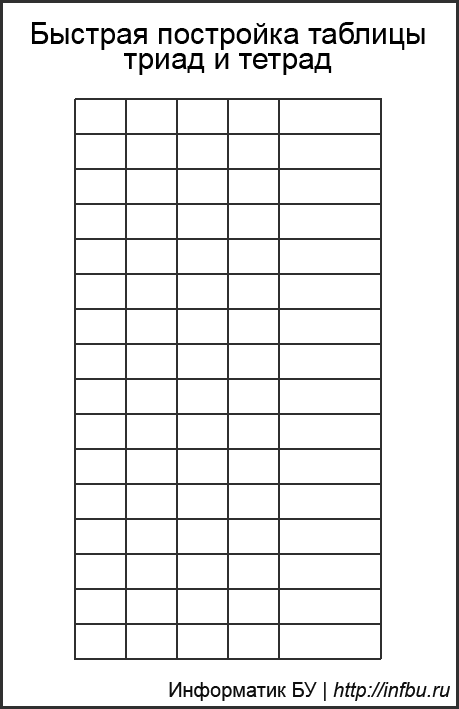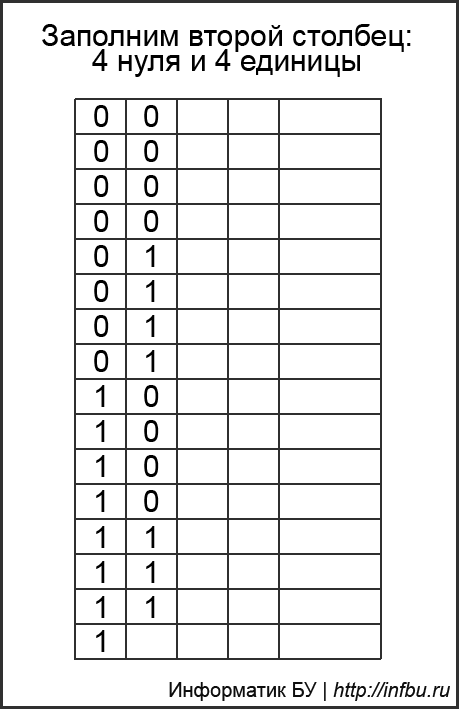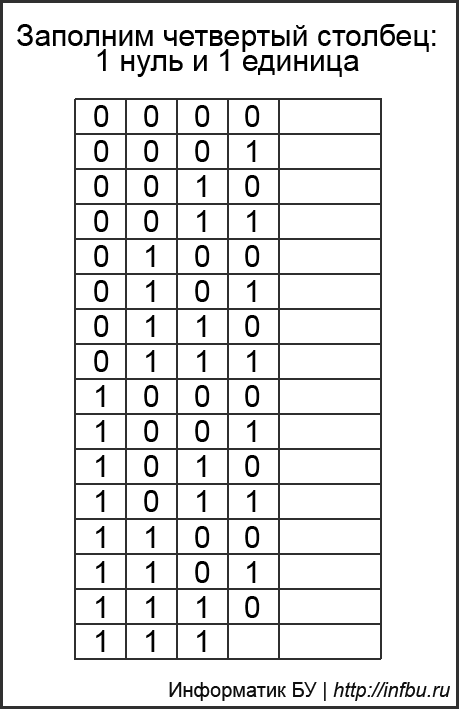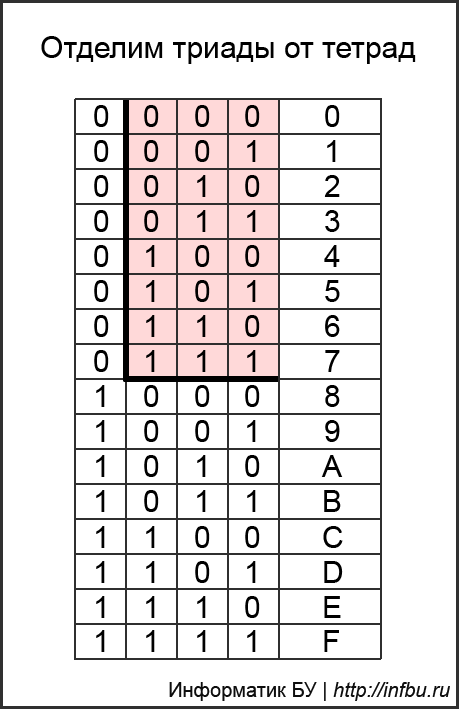
Таблицу триад и тетрад вы можете увидеть, щелкнув по кнопке в правом нижнем углу сайта. Она нужна для быстрого перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную и наоборот.
Многие зазубривают таблицу, но она строится очень просто без зубрёжки:
Перевод чисел из восьмеричной системы счисления в двоичную
Возьмем восьмеричное число 34568
Представим каждый разряд числа в виде триады:
Избавимся от первого незначащего нуля и получим результат:
Перевод чисел из двоичной системы счисления в восьмеричную
Возьмем число 111011012
Разделим его на триады, начиная с правого разряда:
Добавим один незначащий нуль:
Заменим триады значениями из таблицы:
Получается, что 3558 = 111011012
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Возьмем число 15F16
Представим каждый разряд в виде тетрады:
Избавимся от трех первых незначащих нулей и запишем результат:
Получается, что 1010111112 = 15F16
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Возьмем число 100010110111012
Разделим его на тетрады, начиная с правого разряда:
0010 0010 1101 1101
Заменим тетрады значениями из таблицы:
Получается, что 22DD16 = 100010110111012
Триада в информатике это
Переводы в систему счисления с основанием, кратным двойке (2, 8, 16), наиболее эффективно выполнять при помощи триадно – тетрадного метода, суть которого заключается в независимом переводе триад (тетрад) в цифры требуемого 8-ричного (16-ричного) числа.
Для представления одной цифры 8-чной системы используется три двоичных разряда (триада).
| 8-ичная цифра | 10-тичная цифра | Триада | 8-ичная цифра | 10-тичная цифра | Триада |
Тогда для перевода восьмеричного числа в двоичную систему достаточно заменить каждую восьмеричную цифру соответствующей ей двоичной комбинацией из таблицы и избавиться при необходимости от незначащих нулей впереди, например:
Обратный перевод из двоичной системы в восьмеричную заключается в выделении троек двоичных цифр, начиная с конца двоичного числа и добавлении нулей слева для последней тройки, если в ней меньше трех цифр, например:
10101011002 = 1 010 101 1002 = 001 010 101 1002 = 12548
Для представления одной цифры 16-чной системы используется четыре двоичных разряда (тетрада).
| 16-ичная цифра | 10-тичная цифра | Тетрада | 16-ичная цифра | 10-тичная цифра | Тетрада |
| A | |||||
| B | |||||
| C | |||||
| D | |||||
| E | |||||
| F |
Алгоритмы перевода из 16-ричной системы в двоичную аналогичны алгоритмам метода триад с той лишь разницей, что в заменах участвуют не тройки, а четверки двоичных разрядов согласно таблице.
2A97C16 = 0010 1010 1001 0111 11002 = 1010101001011111002
Наиболее удобным способом перевода чисел из восьмеричной системы счисления в 16-ричную и обратно является перевод через двоичную систему. Так, чтобы представить некоторое восьмеричное число в 16-ричной системе, надо сначала по методу триад перевести его в двоичный вид, а затем полученное двоичное число при помощи метода тетрад перевести в 16-ричное. Неполную триаду дополняем слева нулями до полной.
DECA16 = 1101 1110 1100 10102 = 001 101 111 011 001 0102 = 1573128
Аналогично осуществляется перевод чисел из 8-ричной системы счисления в 16-ричную и обратно через двоичную систему. Так, чтобы представить некоторое шестнадцатеричное число в 8-ричной системе, надо сначала по методу тетрад перевести его в двоичный вид, а затем полученное двоичное число при помощи метода триад перевести в 8-ричное. Неполную тетраду дополняем слева нулями до полной.
741528 = 111 100 001 101 0102 = 0111 1000 0110 10102 = 786А16.
Материал представляет собой разработку занятия по информатике в 9 классе
Просмотр содержимого документа
«Урок по информатике «Метод триад и тетрад» (план-конспект)»
План – конспект урока по информатике
по теме: «Перевод чисел из одной системы счисления в другую. Метод триад и тетрад».
Цель урока: ознакомить учащихся с основными правилами перевода чисел из одной системы счисления в другую при помощи метода триад и тетрад.
повторить перевод чисел из одних СС в другие;
научить детей пользоваться таблицей триад и тетрад, показать, как можно получить ее самостоятельно.
развивать личностно-смысловые отношения учащихся к изучаемому предмету;
развитие мышления, памяти;
формирование навыков логического мышления (вывод, анализ, обобщение, выделение главного).
формировать навык самостоятельной работы;
формировать интерес к предмету.
Постановка целей урока.
Проверка домашнего задания – 8 мин.
Проведение самостоятельной работы 12 мин.
Объяснение нового материала. – 12 мин.
Закрепление изученного материала. – 10 мин
1. Организационный момент.
2. Постановка целей урока.
Сегодня мы с вами познакомимся с правилами перевода чисел из одной системы счисления в другую при помощи метода триад и тетрад.
3. Проверка домашнего задания.
Итак, для начала откройте тетради, я проверю наличие домашней работы. А затем мы проверим те правила, которые вы изучили на прошлом уроке.
Правило 1: Перевод целого положительного числа из СС с основанием 10 в систему с основанием q осуществляется его последовательным делением на основание q а до тех пор, пока не получится частное, меньшее q. Последовательными цифрами числа в новой СС будут частное и остатки от деления, начиная с последнего.
Правило 2: Обратный перевод в десятичную СС выполняют, используя позиционную запись данного числа, т. е, представляют число в виде суммы произведений его цифр на соответствующие степени основания.
Правило 3: Перевод правильной дроби из одной СС в другую осуществляется ее последовательным умножением на основание новой системы; при умножаются только дробные части. Дробь в новой СС записывается в виде целых частей получающихся произведений, начиная с первого.
Правило 4: Для перевода неправильных десятичных дробей необходимо выполнить отдельно перевод целой части и дробной.
4. Самостоятельная работа
Ну что же, правила вы выучили хорошо. Теперь можно провести небольшую самостоятельную работу.
Образовательная – познакомить уч-ся с “методом триад и тетрад” для перевода двоичных, восьмеричных и шестнадцатеричных чисел из одной СС в другую.
Развивающая – развивать познавательный интерес учащихся, умения применять полученные знания на практике.
Воспитательная – повысить уровень информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения домашнего упражнения
Уч-ся отвечают на вопросы:
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями двойки, то перевод чисел из этих СС в 2-ую и наоборот прост и основан на методах триад и тетрад. Число делится на триады (тетрады) вправо и влево от десятичной точки. Если крайние триады (тетрады) оказались неполными, они дополняются нулями.
| Алфавит | Триады | Тетрады |
| 000 | 0000 | |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
Упражнение: Выполнить перевод, используя тетрады и триады:
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
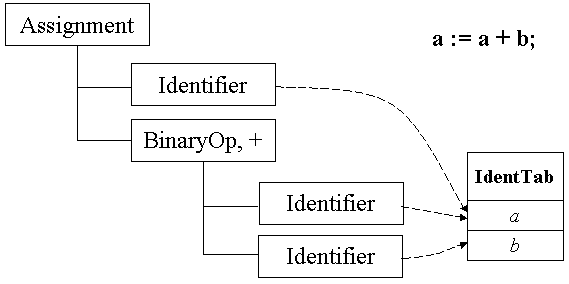
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.