sin x что означает

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

Принцип повтора знаков тригонометрических функций

Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

Функция y = sin x, её свойства и график

п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).

Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.

п.2. Свойства функции y=sinx⁡

2. Функция ограничена сверху и снизу

Область значений \(y\in[-1;1]\)

3. Функция нечётная

4. Функция периодическая с периодом 2π

5. Максимальные значения \(y_=1\) достигаются в точках

Минимальные значения \(y_=-1\) достигаются в точках

Нули функции \(y_<0>=sinx_0=0\) достигаются в точках \(x_0=\pi k\)

6. Функция возрастает на отрезках

Функция убывает на отрезках

7. Функция непрерывна.

п.3. Примеры

Пример 2. Решите уравнение графически:
a) \(sinx=3x\)

Один корень: x = 0

б) \(sinx=2x-2\pi\)

Один корень: x = π

в) \(sinx-\sqrt=0\)
\(sinx=\sqrt\)

Один корень: x = π

Источник

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Синус (sin) угла поворота

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Основные функции тригонометрии

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Источник

Синус, косинус, тангенс и котангенс (ЕГЭ 2022)

Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.

Не так страшен черт, как его малюют!

Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии 🙂 ), начнём с самого начала.

Синус, косинус, тангенс, котангенс — коротко о главном.

Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе

Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе

Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)

Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).

Понятие угла: радиан, градус

Давай для начала разберёмся в понятии угла.

Посмотрим на рисунок.

Вектор \( AB\) «повернулся» относительно точки \( A\) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).

Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!

Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.

Углом в \( 1<>^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac<1><360>\) части окружности.

Таким образом, вся окружность состоит из \( 360\) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен \( 360<>^\circ \).

То есть на рисунке выше изображён угол \( \beta \), равный \( 50<>^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac<50><360>\) длины окружности.

Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.

Ну что, разобрался? Если нет, то давай разбираться по рисунку.

Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.

То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).

Таким образом, длина дуги вычисляется по формуле:

\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.

Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?

Да, для этого надо вспомнить формулу длины окружности. Вот она:

Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).

То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360<>^\circ \).

Соответственно, \( \pi =180<>^\circ \).

Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.

А сколько радиан составляют \( 60<>^\circ \)?

Уловил? Тогда вперёд закреплять:

Тогда смотри ответы:

Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике

Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?

Давай разбираться. Для этого нам поможет прямоугольный треугольник.

Как называются стороны прямоугольного треугольника?

Всё верно, гипотенуза и катеты.

Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))

Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).

Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.

Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?

Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.

В нашем треугольнике \( \sin \beta =\frac\).

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

В нашем треугольнике \( \cos \beta =\frac\).

Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

В нашем треугольнике \( tg\beta =\frac\).

Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).

В нашем треугольнике \( ctg\beta =\frac\).

Эти определения необходимо запомнить!

Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.

А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:

В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).

Тогда убедись, посмотрев на рисунок:

Рассмотрим, к примеру, косинус угла \( \beta \).

По определению, из треугольника \( ABC\): \( \cos \beta =\frac=\frac<4><6>=\frac<2><3>\).

Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac=\frac<6><9>=\frac<2><3>\).

Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.

Если разобрался в определениях, то вперёд закреплять их!

Тогда пробуй сам: посчитай то же самое для угла \( \beta \).

Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac<4><3>\).

Единичная (тригонометрическая) окружность

Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1\).

Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.

Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!

У нас есть целая статья, посвященная ей, которая так и называется «Тригонометрическая (единичная) окружность».

Здесь мы тоже ее разберем довольно подробно.

Как можно заметить, данная окружность построена в декартовой системе координат.

Радиус окружности равен единице.

При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x\) (в нашем примере, это радиус \( AB\)).

Каждой точке окружности соответствуют два числа: координата по оси \( x\) и координата по оси \( y\).

А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?

Для этого надо вспомнить про рассмотренный прямоугольный треугольник.

На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.

Рассмотрим треугольник \( ACG\). Он прямоугольный, так как \( CG\) является перпендикуляром к оси \( x\).

Чему равен \( \cos \ \alpha \) из треугольника \( ACG\)?

Всё верно \( \cos \ \alpha =\frac\).

Кроме того, нам ведь известно, что \( AC\) – это радиус единичной окружности, а значит, \( AC=1\).

Подставим это значение в нашу формулу для косинуса. Вот что получается:

А чему равен \( \sin \ \alpha \) из треугольника \( ACG\)?

Ну конечно, \( \sin \alpha =\frac\)!

Подставим значение радиуса \( AC\) в эту формулу и получим:

Так, а можешь сказать, какие координаты имеет точка \( C\), принадлежащая окружности? Ну что, никак?

А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) — это просто числа?

Какой координате соответствует \( \cos \alpha \)?

Ну, конечно, координате \( x\)!

А какой координате соответствует \( \sin \alpha \)?

Всё верно, координате \( y\)!

Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha )\).

А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)?

Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\frac<\sin \alpha ><\cos \alpha >=\frac\), а \( ctg \alpha =\frac<\cos \alpha ><\sin \alpha >=\frac\).

А что, если угол будет больше \( 90<>^\circ =\frac<\pi ><2>\)?

Вот, к примеру, как на этом рисунке:

Что же изменилось в данном примере?

Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.

Всё верно, придерживаемся соответствующих определений тригонометрических функций:

Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y\); значение косинуса угла – координате \( x\); а значения тангенса и котангенса соответствующим соотношениям.

Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.

Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси \( x\).

До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?

Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.

Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.

Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360<>^\circ \) или \( 2\pi \).

В первом случае, \( 390<>^\circ =360<>^\circ +30<>^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30<>^\circ \) или \( \frac<\pi ><6>\).

Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360<>^\circ \cdot m\) или \( 2\pi \cdot m\) (где \( m\) – любое целое число), соответствуют одному и тому же положению радиус-вектора.

Ниже на рисунке изображён угол \( \beta =-60<>^\circ \).

Этот список можно продолжить до бесконечности.

Все эти углы можно записать общей формулой \( \beta +360<>^\circ \cdot m\) или \( \beta +2\pi \cdot m\) (где \( m\) – любое целое число)

Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:

Вот тебе в помощь единичная окружность:

Возникли трудности? Тогда давай разбираться.

Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.

Ну что же, начнём по порядку: углу в \( 90<>^\circ =\frac<\pi ><2>\) соответствует точка с координатами \( \left( 0;1 \right)\), следовательно:

\( \text\ 90<>^\circ =\frac=\frac<1><0>\Rightarrow \text\ 90<>^\circ \) — не существует;

Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.

Ответы:

\( \displaystyle \sin \ 180<>^\circ =\sin \ \pi =0\) \( \displaystyle \cos \ 180<>^\circ =\cos \ \pi =-1\) \( \text\ 180<>^\circ =\text\ \pi =\frac<0><-1>=0\)

\( \text\ 180<>^\circ =\text\ \pi =\frac<-1><0>\Rightarrow \text\ \pi \) — не существует

\( \sin \ 270<>^\circ =-1\) \( \cos \ 270<>^\circ =0\)

\( \text\ 270<>^\circ =\frac<-1><0>\Rightarrow \text\ 270<>^\circ \) — не существует

\( \text\ 270<>^\circ =\frac<0><-1>=0\) \( \sin \ 360<>^\circ =0\) \( \cos \ 360<>^\circ =1\) \( \text\ 360<>^\circ =\frac<0><1>=0\)

\( \text\ 360<>^\circ =\frac<1><0>\Rightarrow \text\ 2\pi \) — не существует

\( \sin \ 450<>^\circ =\sin \ \left( 360<>^\circ +90<>^\circ \right)=\sin \ 90<>^\circ =1\) \( \cos \ 450<>^\circ =\cos \ \left( 360<>^\circ +90<>^\circ \right)=\cos \ 90<>^\circ =0\)

\( \text\ 450<>^\circ =\text\ \left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<1><0>\Rightarrow \text\ 450<>^\circ \) — не существует

\( \text\ 450<>^\circ =\text\left( 360<>^\circ +90<>^\circ \right)=\text\ 90<>^\circ =\frac<0><1>=0\).

Таким образом, мы можем составить следующую табличку:

Нет необходимости помнить все эти значения!

Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:

А вот значения тригонометрических функций углов в \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\) и \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\), приведённых ниже в таблице, необходимо запомнить:

Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:

Источник

14. Свойства функций синуса, косинуса, тангенса

и котангенса и их графики

14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК

График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:

1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями

координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее

З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох

(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордина-

та соответствующей точки единичной окружности

(рис. 79). Поскольку ординату можно найти для

любой точки единичной окружности (в силу того,

что через любую точку окружности всегда можно

провести единственную прямую, перпендикуляр-

ную оси ординат), то область определения функции

y = sin x — все действительные числа. Это можно за-

писать так: D (sin x) = R.

Для точек единичной окружности ординаты нахо-

дятся в промежутке [–1; 1] и принимают все значения

от –1 до 1, поскольку через любую точку отрезка [–1; 1]

оси ординат (который является диаметром единичной

окружности) всегда можно провести прямую, перпендикулярную оси орди-

нат, и получить точку окружности, которая имеет рассматриваемую орди-

нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].

Это можно записать так: E (sin x) = [–1; 1].

Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окружности является точка A, то есть при

Наименьшее значение функции sin x равно минус единице. Это значение

достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть

при

поэтому ее график симметричен относительно начала координат.

В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом

k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых sin x, то есть ордината соответствующей точки единичной окруж­

ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-

ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).

функции синус положительны (то есть ордината соответствующей точки

единичной окружности положительна) в I и II четвертях (рис. 80). Таким

образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех

x ∈ (2πk; π + 2πk), k ∈ Z.

Значения функции синус отрицательны (то есть ордината соответствую-

щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-

Промежутки возрастания и убывания

Учитывая периодичность функции sin x с периодом T = 2π, достаточно

исследовать ее на возрастание и убывание на любом промежутке длиной

2π, например на промежутке

то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной окружности увеличивается (то есть

sin x ₂ > sin x ₁ ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,

делаем вывод, что она такж е возрастает на каждом из промежутков

Если x ∈ (рис. 81, б), то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной

окружности уменьшается (то есть sin x _{2 1} ), таким образом, на этом промежутке функция sin x убывает. Учитывая

периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой

функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на

промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината

соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на

промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для

построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат

Поскольку мы построили график на

промежутке длиной 2π, то, учитывая

периодичность синуса (с периодом 2π),

повторяем вид графика на каждом про-

межутке длиной 2π (то есть переносим па-

раллельно график вдоль оси Ох на 2πk,

где k — целое число).

Получаем график, который называется

З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,

множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,

описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими

колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль

координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией

времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная

фаза,

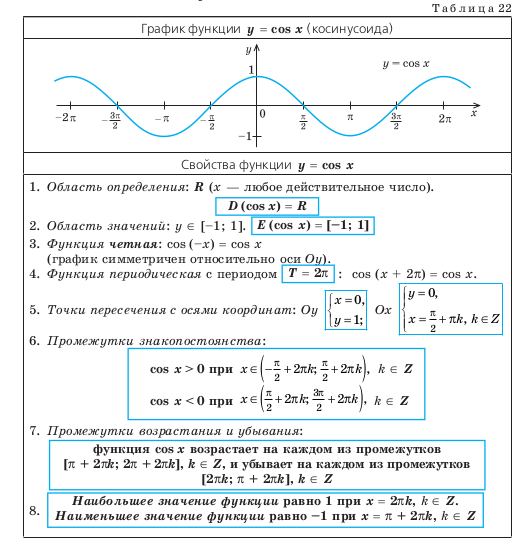
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что значение косинуса — это абсцис-

са соответствующей точки единичной окружности

(рис. 85). Поскольку абсциссу можно найти для лю-

бой точки единичной окружности (в силу того, что

через любую точку окружности, всегда можно про-

вести единственную прямую, перпендикулярную оси

абсцисс), то область определения функции y = cos x —

все действительные числа. Это можно записать так:

D (cos x) = R.

Для точек единичной окружности абсциссы нахо-

дятся в промежутке [–1; 1] и принимают все значе-

ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной

всегда можно провести прямую, перпендикулярную оси абсцисс, и получить

точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:

y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это

зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при

x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.

Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси

Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом

T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.

соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только

тогда, когда на единичной окружности будут выбраны точки C или D, то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции косинус положительны (то есть абсцисса соответствующей точки

единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-

тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех

Значения функции косинус отрицательны (то есть абсцисса соответству-

ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,

поэтому cos x

Промежутки возрастания и убывания

Учитывая периодичность функции cos x (T = 2π), достаточно исследовать

ее на возрастание и убывание на любом промежутке длиной 2π, например

на промежутке [0; 2π].

Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x ₂ > x ₁ ) абсцисса соответствующей точки единичной

окружности уменьшается (то есть cos x _{2 1} ), следовательно, на этом промежутке функция cos x убывает. Учитывая

периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.

Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x ₂ > x ₁ ) аб-

сцисса соответствующей точки единичной окружности увеличивается (то

есть cos x ₂ >cos x ₁ ), таким образом, на этом промежутке функция cos x

возрастает. Учитывая периодичность функции cos x, делаем вывод, что

она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.

Проведенное исследование позволяет построить график функции y = cos x

аналогично тому, как был построен график функ-

ции y = sin x. Но график функции у = cos x можно

также получить с помощью геометрических преоб-

разований графика функции у = sin х, используя

Эту формулу можно обосновать, например, так.

Рассмотрим единичную окружность (рис. 88), отметим на ней точки

Источник