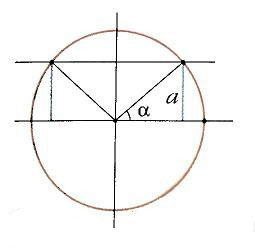
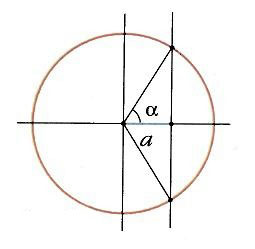
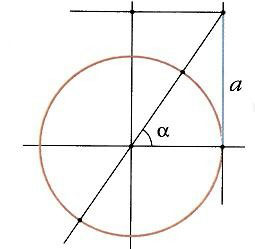
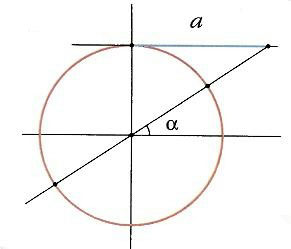
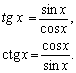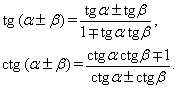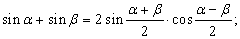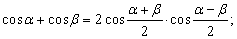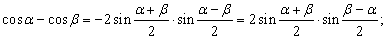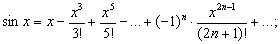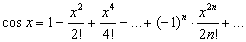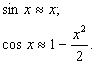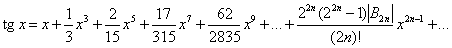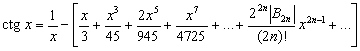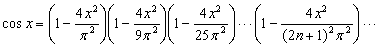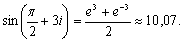sec что это в тригонометрии

СЕКАНС

Смотреть что такое «СЕКАНС» в других словарях:

СЕКАНС — (лат., от secare сечь, рассекать). В тригонометрии: радиус круга, проведенный из центра круга до конца касательной черты, за окружность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СЕКАНС лат. secans, от secare … Словарь иностранных слов русского языка

СЕКАНС — (лат. secans секущая) одна из тригонометрических функций … Большой Энциклопедический словарь

СЕКАНС — [сэ], секанса, муж. (латин secans, букв. рассекающий) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношению гипотенузы к катету, прилежащему к углу. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

СЕКАНС — муж. тригоном. луч (радиус) круга, протянутый до конца касательной черты, за окружность. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

секанс — сущ., кол во синонимов: 1 • функция (49) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

секанс — секанс. Произносится [сэканс] … Словарь трудностей произношения и ударения в современном русском языке

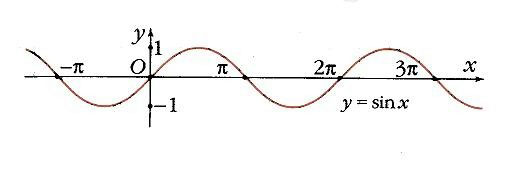
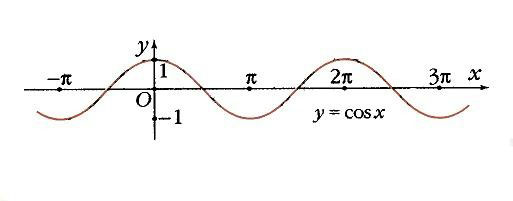
Секанс — Рис. 1 Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса Тригонометрические функции вид элементарных функций. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x),… … Википедия

секанс — а; м. [от лат. secans секущий] Матем. Одна из тригонометрических функций угла, в прямоугольном треугольнике равная отношению гипотенузы к катету, прилежащему к данному углу. * * * секанс (лат. secans секущая), одна из тригонометрических функций … Энциклопедический словарь

Секанс — [лат. secans, здесь секущая (прямая); от seco режу, рассекаю], одна из тригонометрических функций (См. Тригонометрические функции); обозначение sec. В прямоугольном треугольнике С. острого угла называют отношение гипотенузы к катету,… … Большая советская энциклопедия

Источник

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

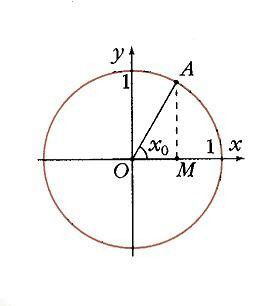
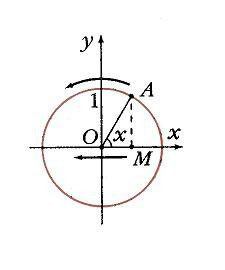
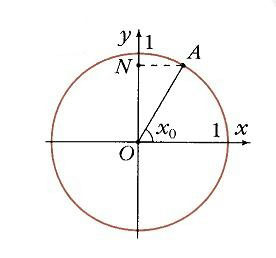
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

Принцип повтора знаков тригонометрических функций

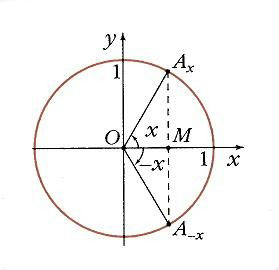
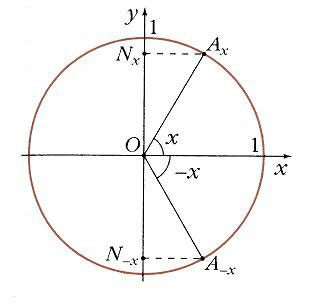
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.

В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.

Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.

Тригонометрический круг

Углы в радианах

Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.

Источник

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

Если — прямоугольные декартовы координаты точки А, то Т. ф. синус и косинус определяются формулами

Остальные Т. ф. могут быть определены формулами

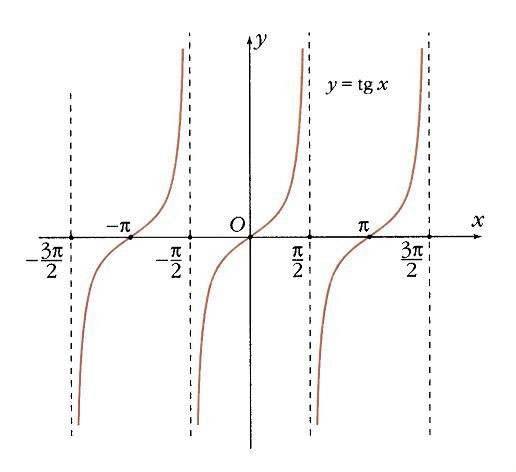
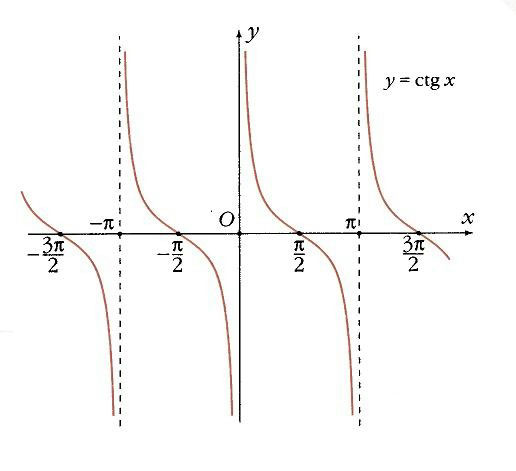
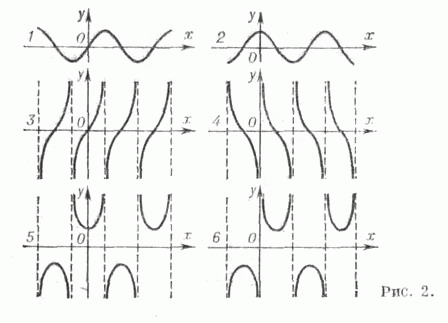
Все Т. ф.- периодические функции. Графики Т. ф. даны на рис. 2.

Основные свойства Т. ф.: область определения, множество значений, четность и участки монотонности приведены в табл.

Каждая Т. ф. в каждой точке своей ооласти определения непрерывна и бесконечно дифференцируема; производные Т. ф.:

Все Т. ф. допускают разложение в степенные ряды:

при

при

Полезное

Смотреть что такое «ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ» в других словарях:

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — (от греческого trigonon треугольник и функция), функции угла. Таковы, например, синус (sin a), косинус (cos a), тангенс (tg a), котангенс (ctg a). Они выражают отношения длин сторон прямоугольного треугольника. Например, sin a отношение длины… … Современная энциклопедия

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса вектора, образующего с положительным направлением оси Ох… … Большой Энциклопедический словарь

Тригонометрические функции — (от греческого trigonon треугольник и функция), функции угла. Таковы, например, синус (sin a), косинус (cos a), тангенс (tg a), котангенс (ctg a). Они выражают отношения длин сторон прямоугольного треугольника. Например, sin a отношение длины… … Иллюстрированный энциклопедический словарь

Тригонометрические функции — Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия

Тригонометрические функции — один из важнейших классов элементарных функций. Для определения Т. ф. обычно рассматривают окружность единичного радиуса с двумя взаимно перпендикулярными диаметрами A A и B B (рис. 1). От точки А по окружности откладываются дуги … Большая советская энциклопедия

тригонометрические функции — функции угла: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec). Их можно определить как отношения длины r и проекций а и b на оси координат радиуса вектора, образующего с положительным направлением оси Ох… … Энциклопедический словарь

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — ф ции угла: синус (sin), косинус (cos), тангенс (tg), котангенс> (ctg), секанс (sес), косеканс(соsес). Т. ф. можно определить как отношения длины г и проекций а и b на оси координат радиус вектора, образующего с положит. направлением оси Ох угол… … Большой энциклопедический политехнический словарь

Обратные тригонометрические функции — (круговые функции, аркфункции) математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: арксинус (обозначение: arcsin) арккосинус (обозначение: arccos)… … Википедия

Обратные тригонометрические функции — аркфункции, круговые функции, решают следующую задачу: найти дугу (число) по заданному значению её тригонометрической функции. Шести основным тригонометрическим функциям соответствуют шесть О. т. ф.: 1) Arc sin х («арксинус x») функция,… … Большая советская энциклопедия

Редко используемые тригонометрические функции — Редко используемые тригонометрические функции функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К… … Википедия

Источник

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ – один из классов элементарных функций.

Функция у = cos х.

Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента x₀ и отсчитать от оси Ox угол x_0, то этому углу на единичной окружности соответствует некоторая точка A (рис. 1) а ее проекцией на ось Ох будет точка М. Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента x₀ сопоставлено значение функции y = cos x₀ как абсциссы точки А. Соответственно точка В (x₀; у₀) принадлежит графику функции у = cos х (рис. 2). Если точка А находится правее оси Оу, то косинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:

Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x, найти на окружности соответствующие точки A_x и А_-x. Как видно на рис. 3 их проекцией на ось Ох является одна и та же точка М. Поэтому

Значит, можно исследовать свойства функции y = cos х на отрезке [0, p ], а затем учесть ее четность и периодичность.

Функция y = sin х.

На единичной окружности углу x₀ соответствует точка А (рис. 7), а ее проекцией на ось Оу будет точка N. Значение функции у₀ = sin x₀ определяется как ордината точки А. Точка В (угол x₀, у₀) принадлежит графику функции y = sin x (рис. 8). Ясно, что функция y = sin x периодическая, ее период равен 2 p :

т.е. синус – функция нечетная, f(–x) = –f(x) (рис. 9).

Если точку A повернуть относительно точки О на угол p /2 против часовой стрелки (другими словами, если угол х увеличить на p /2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,

Иначе, синус – это косинус, «запоздавший» на p /2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p /2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p /2 вправо (рис. 10). Чрезвычайно важное свойство синуса выражается равенством

.

Геометрический смысл равенства виден из рис. 11. Здесь х – это половина дуги АВ, а sin х – половина соответствующей хорды. Очевидно, что по мере сближения точек А и В длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство

Функции у = tg х, у = ctg х. Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:

Котангенс не определен там, где синус равен 0 (когда х = k p ). В остальных точках он монотонно убывает, а прямые х = k p – его вертикальные асимптоты. В точках х = p /2 + k p котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).

Четность и периодичность.

Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:

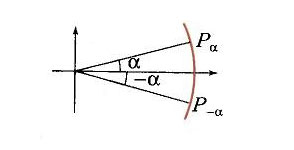
Периодичность синуса и косинуса следует из того, что все точки P _{a + 2k p} , где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P _{a + k p} поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.

Основные свойства тригонометрических функций могут быть сведены в таблицу:

Формулы приведения.

– a + a p – a p + a + a+ a2 p – asin bcos acos asin a–sin a–cos a–cos a–sin acos bsin a–sin a–cos a–cos a–sin asin acos a

1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;

Формулы сложения.

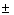
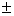
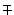
sin ( a b ) = sin a cos b cos a sin b ;

cos ( a b ) = cos a cos b sin a sin b

Формулы кратных углов.

Эти формулы выводятся прямо из формул сложения:

sin 2 a = 2 sin a cos a ;

cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a ;

sin 3 a = 3 sin a – 4 sin 3 a ;

cos 3 a = 4 cos 3 a – 3 cos a ;

Если в формулах двойного аргумента заменить a на a /2, их можно преобразовать в формулы половинных углов:

;

;

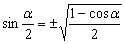
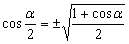
Формулы универсальной подстановки.

Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg ( a /2), это бывает полезно при решении некоторых уравнений:

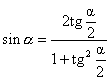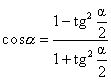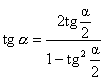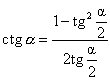Формулы преобразования сумм в произведения и произведений в суммы.

До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:

2 sin a sin b = cos ( a – b ) – cos ( a + b );

2 cos a cos b = cos ( a – b ) + cos ( a + b );

2 sin a cos b = sin ( a – b ) + sin ( a + b ).

Формулы для функций тангенса и котангенса можно получить из вышеприведенных.

Формулы понижения степени.

Из формул кратного аргумента выводятся формулы:

С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.

Производные и интегралы тригонометрических функций
(sin x)` = cos x;	(cos x)` = –sin x;
(tg x)` = 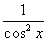;	(ctg x)` = – ;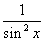
т sin x dx = –cos x + C;	т cos x dx = sin x + C;
т tg x dx = –ln |cos x| + C;	т ctg x dx = ln |sin x| + C;

Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.

Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.

Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:

Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:

Функции sin x и cos x могут быть представлены в виде бесконечных произведений:

(эта формула была получена Эйлером в 1740);

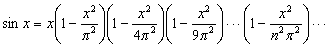
Тригонометрические функции комплексного аргумента

определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x, если вместо x поставить z:

,

.

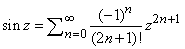
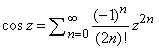
Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.

Тангенс и котангенс определяются формулами:

,

.

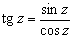
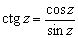
Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p /2 + p n, полюсы ctg z и cosec z – также простые и находятся в точках z = p n, n = 0, ±1, ±2,…

Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,

т.е. четность и нечетность сохраняются. Сохраняются и формулы

т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.

Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:

;

;

.

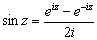
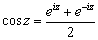
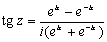
Обратно, e iz выражается через cos z и sin z по формуле:

Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.

Тригонометрические функции также можно выразить через гиперболические функции:

z = –i sh iz, cos z = ch iz, z = –i th iz.

где sh, ch и th – гиперболические синус, косинус и тангенс.

Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:

Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:

Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим. Такие уравнения настолько часто встречаются, что методы их решения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.

Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а. Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическими функциями или просто аркфункциями.

Обратные тригонометрические функции.

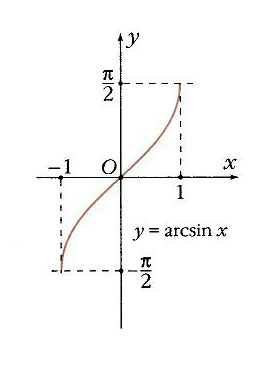
Для sin х, cos х, tg х и ctg х можно определить обратные функции. Они обозначаются соответственно arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x. По определению, arcsin х есть такое число у, что

Аналогично и для других обратных тригонометрических функций. Но такое определение страдает некоторой неточностью.

Если отразить sin х, cos х, tg х и ctg х относительно биссектрисы первого и третьего квадрантов координатной плоскости, то функции из-за их периодичности становятся неоднозначными: одному и тому же синусу (косинусу, тангенсу, котангенсу) соответствует бесконечное количество углов.

Так же решаются другие простейшие тригонометрические уравнения:

где п = 0, ±1, ±2. (рис. 16);

где п = 0, ±1, ±2. (рис. 17);

где п = 0, ±1, ±2. (рис. 18).

Основные свойства обратных тригонометрических функций:

arcsin х (рис. 19): область определения – отрезок [–1, 1]; область значений – [– p /2, p /2], монотонно возрастающая функция;

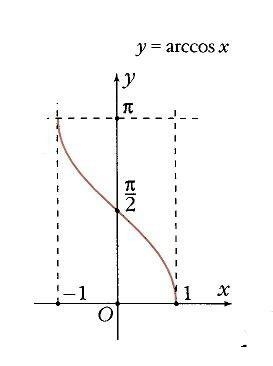
arccos х (рис. 20): область определения – отрезок [–1, 1]; область значений – [0, p ]; монотонно убывающая функция;

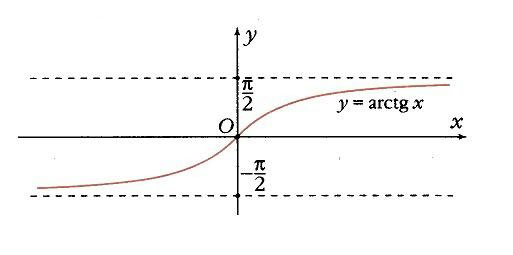
arctg х (рис. 21): область определения – все действительные числа; область значений – интервал (– p /2, p /2); монотонно возрастающая функция; прямые у = – p /2 и у = p /2 – горизонтальные асимптоты;

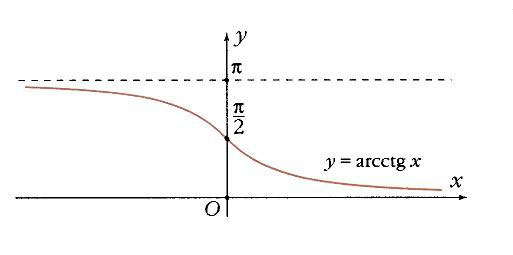
arcctg х (рис. 22): область определения – все действительные числа; область значений – интервал (0, p ); монотонно убывающая функция; прямые y = 0 и у = p – горизонтальные асимптоты.

Т.к. тригонометрические функции комплексного аргумента sin z и cos z (в отличие от функций действительного аргумента) принимают все комплексные значения, то и уравнения sin z = a и cos z = a имеют решения для любого комплексного a:

,

.

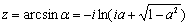
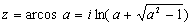
Функции tg z и ctg z принимают все комплексные значения, кроме ±i: уравнения tg z = a, ctg z = a имеют решения для любого комплексного числа a № ± i:

,

.

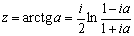
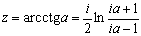
Для любого z = x + iy, где x и y – действительные числа, имеют место неравенства

из которых при y ® Ґ вытекают асимптотические формулы (равномерно относительно x)

Кочетков Е.С., Кочеткова Е. С. Алгебра и элементарные функции, ч. 1–2, М., 1966
Шабат Б.В. Введение в комплексный анализ. М., 1969

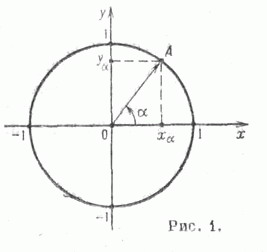
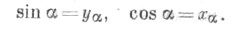
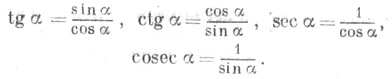
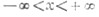
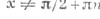
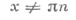
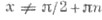
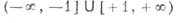
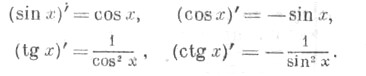
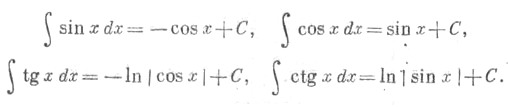
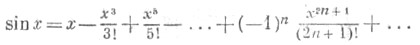
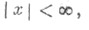
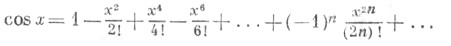
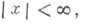
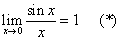Источник