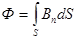qvbsina что за формула
Qvbsina что за формула
Явление электромагнитной индукции.
Открытое в 1831 году Фарадеем явление электромагнитной индукции состоит в том, что в любом замкнутом контуре при изменении магнитного потока через поверхность, ограниченную этим контуром, возникает электродвижущая сила, величина которой пропорциональна скорости изменения магнитного потока:
В проводящем контуре существование ЭДС индукции приводит к появлению индукционного тока. Знак минус в формуле соответствует правилу Ленца, согласно которому направление индукционного тока всегда таково, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
ЭДС индукции в движущихся проводниках.
Изменение магнитного потока через контур, вызывающее появление ЭДС индукции, может происходить как за счет изменения магнитного поля, так и за счет изменения ориентации и формы контура.
В тех случаях, когда магнитное поле не изменяется во времени, а магнитный поток через контур изменяется из-за движения проводников контура в магнитном поле (изменения площади контура S ), причиной возникновения ЭДС индукции является сила Лоренца.
С другой стороны, за время D t площадь контура изменяется на величину D S=l V D t, а магнитный поток : D Ф=B V lsina D t.
Итак, ЭДС индукции будет равна: E = BVlsina
ЭДС индукции в неподвижных проводниках.
Остаётся допустить, что в области, где существует переменное магнитное поле, возникает электрическое поле, которое и обусловливает возникновение индукционного тока в замкнутом контуре, т.е. работа сил этого электрического поля поля по замкнутому контуру уже не равна нулю. Поэтому, в отличие от потенциального электростатического поля, это электрическое поле называют вихревым.
Итак, переменное магнитное поле создает в каждой точке пространства
Если по катушке идет п epe м e нный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет ток. Это явление называют самоиндукцией. При самоиндукции проводящий контур играет двоякую роль: по нему протекает ток, создающий переменное магнитное поле, и в нем же возникает ЭДС индукции.
Явление самоиндукции подобно явлению инерции в механике. За счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Модуль B вектора индукции магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф
где L- индуктивность контура. Это физическая величина, числено равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с. Зависит от числа витков, размеров, формы и сердечника катушки. Измеряется в генри (Гн).
Используя закон электромагнитной индукции и формулу для индуктивности контура, получаем равенство:
Действие магнитного поля на движущийся заряд



Опыт показывает, что магнитное поле действует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренцаи выражается формулой
F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки:если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q
Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца:
F=QE + Q[vB].
Это выражение называется формулой Лоренца.Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
Закон Ома для участка цепи и полной цепи: формулы и определения
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac <\varepsilon>
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Основные формулы. Связь магнитной индукции B с напряженностью H магнитного поля
ЭЛЕКТРОМАГНЕТИЗМ
Связь магнитной индукции B с напряженностью H магнитного поля
B = mm0H,
B = m0H.
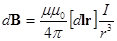

Магнитная индукция в центре кругового тока
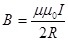
Магнитная индукция на оси кругового тока
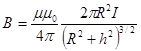
Магнитная индукция поля прямого тока
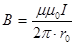
Магнитная индукция поля, создаваемого отрезком провода с током
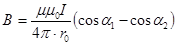
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция,
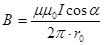
Магнитная индукция поля соленоида B = mm0nI,
Сила, действующая на провод с током в магнитном поле (закон Ампера),
F = I[l B], или F = I×B×l×sina,
dF = I[dl B].
Магнитный момент плоского контура с током
pm = nIS,
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле,
M = [pm B], или M = pm Bsina,
где a- угол между векторами pm и B.
Потенциальная энергия (механическая) контура с током в магнитном поле
Сила Лоренца F = Q[vB], или F=QvBsina,
а) в случае однородного магнитного поля и плоской поверхности
Ф = BScosa или Ф =Bn S,
б) в случае неоднородного поля и произвольной поверхности
(интегрирование ведется по всей поверхности).
Потокосцепление (полный поток) Y = NФ.
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Работа по перемещению замкнутого контура в магнитном поле
ЭДС индукции 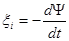
Разность потенциалов на концах провода, движущегося со скоростью v в магнитном поле, U = B×l×v×sina,
Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего контур,
Q = DФ/R, или Q = NDФ/R = DY/R,
Индуктивность соленоида L = Ф/I.
ЭДС самоиндукции 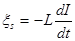
Индуктивность соленоида L = mm0 n 2 V,
Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:
Энергия магнитного поля 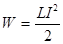
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Электротехника
вторник, 22 июня 2010 г.
МАГНИТНОЕ ПОЛЕ. ЗАКОН ПОЛНОГО ТОКА
РАЗДЕЛ 2. ЭЛЕКТРОМАГНЕТИЗМ И ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЛЕКЦИЯ 11. МАГНИТНОЕ ПОЛЕ. ЗАКОН ПОЛНОГО ТОКА
Магнитное поле – это материя, которая окружает движущиеся заряженные частицы, неразрывно с ними связана и определяется по силовому воздействию на движущиеся заряженные тела.
Силы в магнитном поле:
1. Сила Ампера – это сила, которая действует на проводник с током, помещенный в магнитное поле.
Направление силы Ампера можно определить по правилу левой руки: если четыре вытянутых пальца левой руки расположить по току проводнике так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, то отогнутый на 90 0 большой палец укажет направление силы Ампера.
2. Сила Лоренца – это сила, действующая со стороны магнитного поля на любую заряженную частицу.
Направление силы Лоренца определяется по правилу левой руки: если левую руку расположить по скорости движения положительно заряженной частицы, против движения отрицательной, так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, то отогнутый на 90 0 большой палец укажет направление силы Лоренца.
2. Определить направление силы Лоренца, действующей на частицу в магнитном поле:
Характеристики магнитного поля:
1. По интенсивности и направленности магнитное поле характеризуется вектором магнитной индукции – В [1Тл].
Модуль вектора В равен отношению максимального значения модуля силы Ампера к силе тока и длине проводника: B = FAmax / Il
Направление вектора магнитной индукции определяется по правилу буравчика: если буравчик с правой нарезкой расположить так, чтобы поступательное движение острия буравчика совпадало с направлением тока в проводнике, то вращательное движение рукоятки буравчика укажет направление вектора магнитной индукции.
3. Определить направление вектора магнитной индукции, если ток в проводнике направлен следующим образом:
2. Интегральной характеристикой магнитного поля служит магнитный поток – Ф[1 Тл]. Он представляет собой поток вектора магнитной индукции сквозь данную замкнутую поверхность:
а) Ф = В S б) Ф = В Scos a
3. Характеристикой магнитного поля, не учитывающей влияния среды, является напряженность магнитного поля – Н [ A /м]. B = m 0Н
4. Свойство тока возбуждать магнитное поле называется магнитодвижущей силой – F [1 A ]: F = I – если мы рассматриваем проводник с током; F = NI – если мы рассматриваем катушку с током, где N – число витков катушки.
5. Магнитное напряжение – U м [1 A ] : UM = Hl
Работа сил магнитного поля:
1. Пусть в магнитном поле под действием силы Ампера перемещается проводник с током толщиной b на расстояние своей толщины. Необходимо определить работу магнитного поля по перемещению проводника с током (рис. а):
Вывод: работа электромагнитных сил, затраченная на перемещение проводника с током, равна произведению тока в проводнике на изменение магнитного потока, сцепленного с этим проводником.
2. Рассмотрим перемещение контура толщиной d на величину своей толщины в магнитном поле и определим работу поля по перемещению этого контура (рис. б)
Вывод: работа магнитного поля по перемещению контура не зависит от формы этого контура. Всякий контур с током стремиться занять в магнитном поле такое положение, при котором магнитный поток, пронизывающий контур максимален.
Закон полного тока
Полным током называется алгебраическая сумма токов, пронизывающих поверхность, ограниченную замкнутым контуром.
Положительными считаются токи, направления которых совпадают с поступательным движением буравчика, рукоятка которого вращается по обходу контура.
Закон полного тока (первая формулировка): магнитодвижущая сила вдоль контура равна полному току, который проходит сквозь поверхность, ограниченную данным контуром: F = S I
Закон полного тока (вторая формулировка): циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему поверхность, ограниченную этим контуром: S I = ò Н l dl