подобие геометрических фигур в жизни

Проектно-исследовательская работа по геометрии «Применение подобия треугольников и фигур в жизни «

Просмотр содержимого документа
«Проектно-исследовательская работа по геометрии «Применение подобия треугольников и фигур в жизни «»

Применение подобия треугольников и фигур в жизни

Работу выполнила: Олейникова Дарья

Руководитель: учитель математики

Понятие подобия треугольников

Признаки подобия треугольников

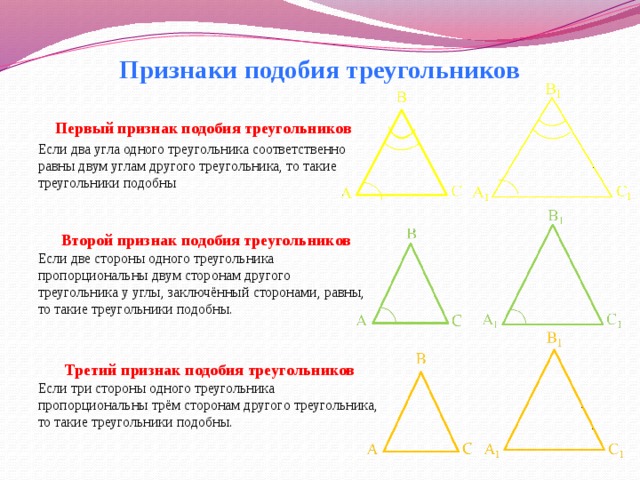
Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника у углы, заключённый сторонами, равны, то такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

За шесть веков до нашей эры греческий мудрец Фалес Милетский

вычислил высоту египетской пирамиды, измерив длину её тени.

Как это было, рассказывается в книге Я.И.Перельмана

Фалес, говорит предание, избрал день и час,

когда длина собственной его тени

равнялась его росту. В этот момент высота пирамиды

должна также равняться

Вот, пожалуй, единственный

случай, когда человек

извлёк пользу из своей тени.

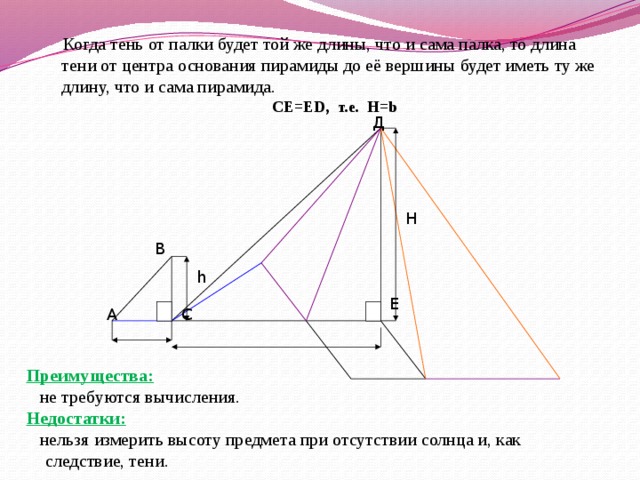
Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида.

не требуются вычисления.

Жюль Верн Это писатель, предвосхитивший возможности современного технического прогресса. Из 108 гипотез писателя 64 были реализованы. Увлекавшийся идеями технического прогресса, Ж.Верн был поэтом природы.

В романе Жюля Верна «Таинственный остров» описан один из способов измерения высоких предметов.

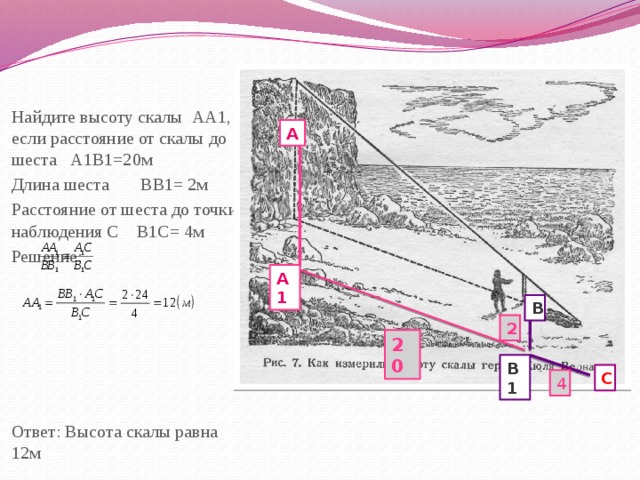
Найдите высоту скалы АА1, если расстояние от скалы до шеста А1В1=20м

Длина шеста ВВ1= 2м

Расстояние от шеста до точки наблюдения С В1С= 4м

Ответ: Высота скалы равна 12м

Нахождения четвертого неизвестного члена

так как приходится

Определение высоты предмета

 АВD подобен  EFD (по двум углам):

В подобных треугольниках сходственные стороны пропорциональны:

измерения в любую погоду;

одежда будет чистой;

нужно специальное приспособление: зеркало.

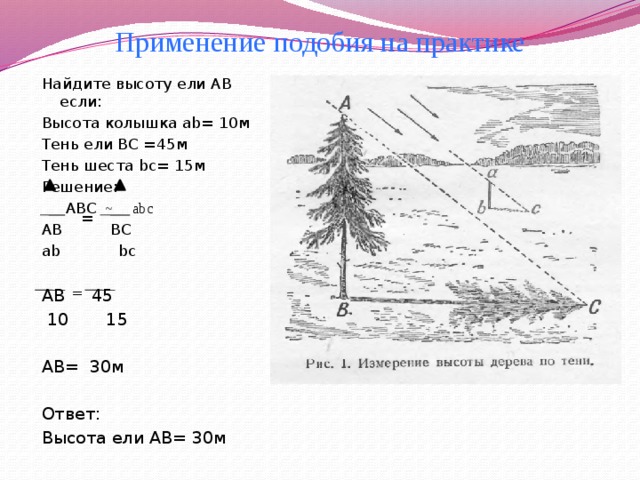
Применение подобия на практике

Найдите высоту ели АВ если:

Высота колышка ab= 10м

Задача – измерение расстояния до недоступной точки.

Чтобы найти ширину реки АВ необходимо поставить колышек С на продолжение АВ, вдоль берега отмерить на прямой CF перпендикулярной АС, расстояние одно в несколько раз меньше другого. Например : отмеряют FE в четыре раза меньше ЕС. По направлению FG, перпендикулярному к FD отыскивают точку Н из которой точка Е перекрывает точку А . Треугольники АСЕ и EFH подобны (объясните почему). Из подобия треугольников следует пропорция AC:FH=CE:EF=4:1.

Значит, измерив FH, можно узнать искомую ширину реки.

CE:EF=4:1 FH=6 м, BC=4 м

Решение задачи на конкретном примере

СС1- 8м, расстояние от ели до

ВС- 1 м, расстояние от меня до

точки пересечения гипотенузы с

Ответ: высота ели = 13,5м

Подобие в жизни и архитектуре

Всемирный торговый центр в Нью-Йорке

комплекс из семи зданий, спроектированный Минору Ямасаки и официально открытый 4 апреля 1973 года в Нью-Йорке (США). Архитектурной доминантой комплекса были две башни, каждая по 110 этажей — Северная (высотой 526,3 м) и Южная (высотой 415 м). 11 сентября 2001 года комплекс ВТЦ был разрушен в результате террористической атаки.

Всемирный торговый центр в Коломбо

самое высокое законченное здание в Шри-Ланке. Высота — 152 метра, таким образом башни занимают третье место по высоте среди башен-близнецов в Южной Азии. Он один из 320 Всемирных торговых центров в 90 странах мира.

Башни Петронас в Куала-Лумпуре

88-этажный небоскрёб. Высота — 451,9 метров. Находится в столице Малайзии Куала-Лумпуре. В проектировании небоскрёба участвовал премьер-министр Малайзии Махатхир Мохамад, который предложил построить здания в «исламском» стиле. Поэтому в плане комплекс представляет собой две восьмиконечные звезды.

Торрес-де-Санта-Крус в Испании

пара небоскрёбов, представляющих собой жилые башни-близнецы. Небоскрёбы расположены в городе Санта-Крус-де-Тенерифе (Канарские острова, Испания). Первое здание было построено в 2004 году, а второе — в 2006 году.

Башни-близнецы Банка Германии

два небоскрёба, высотой по 155 м.,являющиеся штаб-квартирой Банка Германии, находящиеся во Франкфурте-на-Майне, Германия. Занимают 80 место по высоте в Европе, 53 место в Евросоюзе, 11 место в Германии и 10 место во Франкфурте-на-Майне.

«Ворота Европы» в Мадриде

Самый большой макет центральной части Москвы

Это та же Москва только уменьшенная в 400 раз

Готовая часть нового архитектурного макета Москвы выставлена в павильоне №75 на Выставке достижений народного хозяйства.

Завершить работу над макетом планируется к 2017 году, он сможет войти в Книгу рекордов Гиннеса как самый большой макет города.

Площадь этого макета — 70 квадратных метров, 6500 зданий.

Общая площадь макета после окончания всех работ составит 950 квадратных метров, на нем будет представлена часть города, охватывающая Третье транспортное кольцо, все железнодорожные вокзалы, а также территорию Воробьевых гор и активно развивающиеся территории промышленной зоны ЗИЛ(Завод Имени Лихачева).

Источник

«Подобие фигур в жизни»

Выбранный для просмотра документ pril1.ppt

Описание презентации по отдельным слайдам:

Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей. Вот один пример из «Устава ратных, пушечных и других дел, касающихся до военной науки»:

За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.

Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. СЕ=ED, т.е. H=b Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

«Таинственный остров» (фр. L’Île mystérieuse) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. Является продолжением известных произведений Верна «20000 лье под водой» и «Дети капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.

Нахождения четвертого неизвестного члена пропорции. Преимущества: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить высоту предмета не испачкавшись, так как приходится ложиться на землю.

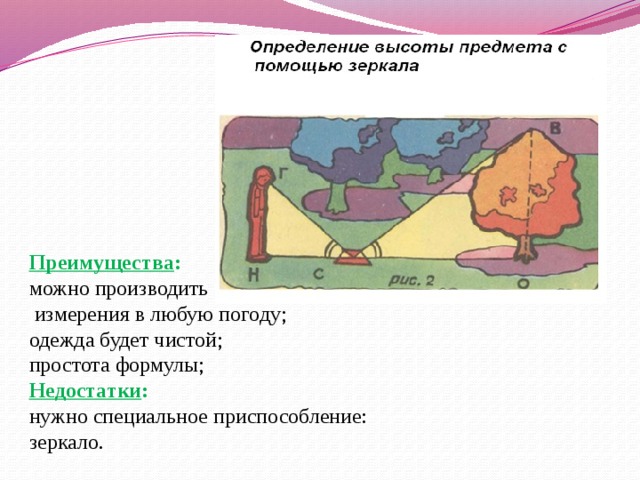
Преимущества: можно производить измерения в любую погоду; одежда будет чистой; простота формулы; Недостатки: нужно специальное приспособление: зеркало.

По построению  АВС подобен  А1В1С1 (по двум углам). В подобных треугольниках сходственные стороны пропорциональны: А В С А1 В1 С1

Нахождение ширины озера Длина тени земного шара

Выбранный для просмотра документ Природа говорит языком математики.doc

Природа говорит языком математики.

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.

При помощи подобных треугольников можно измерить огромные расстояния и высоты используя подручные средства, т.е. мы будем решать две задачи:

определение высоты предмета;

определение расстояния до недоступного объекта.

Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Вот один пример. Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.

Рассмотрим несколько случаев из истории и литературы.

1. Определение высоты предмета по длине его тени.

Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.

Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.

Я хочу прочитать вам эту маленькую притчу.

«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.

— Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

Определение высоты пирамиды по длине ее тени.

АВС подобен D СDE (по двум углам):

ВСА= СED=90°;

АВС= СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

В подобных треугольниках сходственные стороны пропорциональны:

.

Таким образом, Фалес нашел высоту пирамиды.

Преимущества способа Фалеса:

не требуются вычисления.

нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

2. Определение высоты предмета по шесту.

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».

Читаем отрывок из романа.

— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны.

— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.

Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

По окончании измерений инженер составил следующую запись:

Н 333,33

Значит, высота гранитной стены равнялась приблизительно 333 футам».

Преимущества способа Жюль Верна:

— можно производить измерения в любую погоду;

нельзя измерить, высоту предмета не испачкавшись, так как приходится ложиться на землю.

3. Определение высоты предмета.

Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.

Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.

АВD подобен D EFD (по двум углам):

ВАD = FED=90°;

АDВ = EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

; .

Таким образом, найдена высота объекта.

4. Определение расстояния до недоступного объекта.

Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1 ).

6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).

7. Дополнительный материал. Слайд 29-30

Источник

Научно-исследовательский проект «Подобные фигуры вокруг нас»

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ САМАРСКОЙ ОБЛАСТИ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА

«ЦЕНТР ОБРАЗОВАНИЯ» С.ШИГОНЫ

МУНИЦИПАЛЬНОГО РАЙОНА ШИГОНСКИЙ САМАРСКОЙ ОБЛАСТИ

«Подобные фигуры вокруг нас»

Митина Анастасия, 8 «В» класс

учитель математики высшей категории

Глава 1. Подобные фигуры вокруг нас

1.1. Из истории подобия

1.2. Понятие подобия

1.3.Способы измерения предметов с применением подобия

1.3.1. Первый способ измерения высоты предмета

1.3.2. Второй способ измерения высоты предмета

1.3.3. Третий способ измерения высоты предмета

Глава 2. Использование подобия треугольников на практике

2.1. Измерение высоты объекта

2.1. 2. С помощью шеста

2.1.3. С помощью зеркала

2.1.4. Как поступил сержант

2.1.5. Не приближаясь к дереву

2.2.1. Способы очистки водоемов

2.2.2. Измерение ширины пруда

Порой не замечаем мы,

Мы говорим « Подобен Божеству»,

Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, полученные из наблюдений и опытов. Почти все великие ученые древности и средних веков были выдающимися геометрами. Девиз древней школы был: «Не знающие геометрии не допускаются!»

В наше время геометрические знания по-прежнему находят широкое применение в строительстве, архитектуре, искусстве, а также во многих отраслях промышленности. На уроках геометрии мы изучили тему «Подобие треугольников», и меня заинтересовал вопрос, как данную тему можно применить на практике.

Вспомните произведение Л. Керолла «Алиса в стране чудес». Какие изменения происходили с главной героиней: то она вырастала до нескольких футов, то уменьшалась до нескольких дюймов, всегда оставаясь, впрочем, сама собой. О каком преобразовании с точки зрения геометрии идет речь? Конечно, о преобразовании подобия.

Нахождение области применения подобия треугольников в жизни человека.

1.Изучить научную литературу по данной теме.

2.Показать применение подобия треугольников на примере измерительных работ.

Гипотеза. С помощью подобия треугольников можно выполнять измерения реальных объектов.

Методы исследования: поиск, анализ, математическое моделирование.

Глава1. Подобные фигуры вокруг нас

1.1.Из истории подобия

В основе подобия фигур лежит принцип отношения и пропорции. Идея отношения и пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские дворцы и другие памятники древности. Многие обстоятельства, в том числе особенности архитектуры, требования удобства, эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин. В «Московском» папирусе при рассмотрении отношения большего катета к меньшему в одной из задач на прямоугольный треугольник применяется специальный знак для понятия «отношение». В «Началах» Евклида учение об отношениях излагается дважды. В VII книге содержится арифметическая теория. Она относится только к соизмеримым величинам и к целым числам. Эта теория создана на основе практики действия с дробями. Евклид применяет ее для исследования свойств целых чисел. В V книге излагается общая теория отношений и пропорций, разработанная Евдоксом. Она лежит в основе учения о подобии фигур, изложенного в VI книге «Начал», где находится определение: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».

Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.

До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.

В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобными.

У всех подобных фигур одинаковые формы, но разные размеры.

Определение: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Замечание 1: Равные треугольники подобны с коэффициентом 1.

Замечание 2: При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны.

Замечание 3: Требования, которые перечислены в определении подобных треугольников, являются избыточными.

Свойства подобных треугольников

Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

1.3.Способы измерения предметов с применением признаков подобия

1.3.1. Первый способ измерения высоты предмета

В солнечный день не составляет труда измерение высоты предмета, предположим дерева, по его тени. Необходимо только, взять предмет (например, палку) известной длины и установить ее перпендикулярно поверхности. Тогда от предмета будет падать тень. Зная высоту палки, длину тени от палки, длину тени от предмета, высоту которого мы измеряем, можно определить высоту предмета. Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу.

«Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мгновению распахнули перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы.

Кто ты? –спросил верховный жрец.

Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта.

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту. Что сказал Фалес?

Слова Фалеса : Когда тень от палки стала той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины имеет ту же длину, что и сама пирамида.

1.3.2.Второй способ измерения высоты предмета

Этот способ был предметно описан у Жюля Верна в романе «Таинственный Остров». Этот способ можно применять, когда нет солнца и не видно тени от предметов. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от предмета, чтобы лежа можно было видеть верхушку предмета на одной прямой линии с верхней точкой шеста. Тогда высоту предмета можно найти, зная длину линии, проведенной от вашей головы до основания предмета.

Вам понадобится для этого инструмент? – спросил Герберт.

Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

«-Тебе знакомы зачатки геометрии? – спросил он Герберта, поднимаясь с земли. Помнишь свойства подобных треугольников

-Их сходственные стороны пропорциональны.

-Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. …Если мы измерим два расстояния: расстояние от колышка до основания шеста и расстояние от колышка до основания стены, то, зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, т. е. высоту стены. Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись:

15 : 500 = 10 : х; 500 х 10 = 5000; 5000 : 15 = 333,3.

Значит, высота гранитной стены равнялась 333 футам.

1.3.3.Третий способ определение высоты предмета по зеркалу.

Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до зеркала больше, чем расстояние от зеркала до вас. Помните: угол падения равен углу отражения (закон отражения).

 АВD подобен EFD (по двум углам):

АDВ =EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

Источник