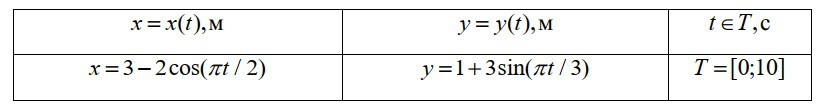plot2d scilab что это
plot2d
Syntax
Arguments
a real matrix or vector. If omitted, it is assumed to be the vector 1:n where n is the number of curve points given by the y parameter.
a real matrix or vector.
sets the style for each curve. The associated value should be a real vector with integer (positive or negative) values.
controls the display of captions.
strf is a string of length 3 «xyz» (by default strf= «081» )
sets the curves captions. The associated value should be a character string.
sets the axes labels and tics definition. The associated value should be a real vector with four integer entries [nx,Nx,ny,Ny].
controls the computation of the actual coordinate ranges from the minimal requested values. The associated value should be an integer ranging from 0 to 8.
specifies how the axes are drawn. The associated value should be an integer ranging from 0 to 5 or 9 (default value).
Description
plot2d plots a set of 2D curves. If you are familiar with Matlab plot syntax, you should use plot.
The arguments should be used to customize the plot
This option may be used to specify how the curves are drawn. If this option is specified, the associated value should be a vector with as many entries as curves.
if style(i) is strictly positive, the curve is drawn as plain line and style(i) defines the index of the color used to draw the curve (see getcolor). Note that the line style and the thickness can be set through the polyline entity properties (see polyline_properties).
Piecewise linear interpolation is done between the given curve points.
if style(i) is negative or zero, the given curve points are drawn using marks, abs(style(i)) defines the mark with id used. Note that the marks color and marks sizes can be set through the polyline entity properties (see polyline_properties).
is a string of length 3 «xyz» (by default strf= «081» )
controls the display of captions.
controls the computation of the actual coordinate ranges from the minimal requested values. Actual ranges can be larger than minimal requirements.
no computation, the plot use the previous (or default) scale
from the min/max of the x, y data
built for an isometric scale from the rect arg
built for an isometric plot from the min/max of the x, y data
enlarged for pretty axes from the rect arg
enlarged for pretty axes from the min/max of the x, y data
like y=1 but the previous plot(s) are redrawn to use the new scale
like y=2 but the previous plot(s) are redrawn to use the new scale
controls the display of information on the frame around the plot. If axes are requested, the number of tics can be specified by the nax optional argument.
nothing is drawn around the plot.
axes are drawn, the y=axis is displayed on the left.
the plot is surrounded by a box without tics.
axes are drawn, the y=axis is displayed on the right.
axes are drawn centred in the middle of the frame box.
The curve captions are drawn on below the x-axis. This option is not flexible enough, use the captions or legend functions preferably.
This option may be used to set the minimal bounds requested for the plot. If this option is specified, the associated value should be a real vector with four entries:
The axes boundaries can also be customized through the axes entity properties (see axes_properties).
Ny and ny give similar information for the y-axis.
If axesflag option is not set nax option supposes that axesflag option has been set to 9.
This option may be used to control the computation of the actual coordinate ranges from the minimal requested values. Actual ranges can be larger than minimal requirements.
no computation, the plot use the previous (or default) scale.
The actual range is the range given by the rect option.
The actual range is computed from the min/max of the x and y data.
The actual range is the range given by the rect option and enlarged to get an isometric scale.
The actual range is computed from the min/max of the x and y data and enlarged to get an isometric scale.
The actual range is the range given by the rect option and enlarged to get pretty axes labels.
The actual range is computed from the min/max of the x and y data and enlarged to get pretty axes labels.
like frameflag=1 but the previous plot(s) are redrawn to use the new scale. Used to add the current graph to a previous one.
like frameflag=2 but the previous plot(s) are redrawn to use the new scale. Used to add the current graph to a previous one.
like frameflag=8 but the range is enlarged to get pretty axes labels. This is the default value.
The axes boundaries can also be customized through the axes entity properties (see axes_properties)
This option may be used to specify how the axes are drawn. The associated value should be an integer ranging from 0 to 5 :
nothing is drawn around the plot (axes_visible=[«off» «off»];box=»off»).
axes are drawn, the y-axis is displayed on the left (axes_visible=[«on» «on»];box=»on»,y_location=»left»).
the plot is surrounded by a box without tics (axes_visible=[«off» «off»];box=»on»).
axes are drawn, the y-axis is displayed on the right (axes_visible=[«on» «on»];box=»off»,y_location=»right»).
axes are drawn centered in the middle of the frame, the box being not drawn (axes_visible=[«on» «on»];box=»off»,x_location=»middle», y_location=»middle»).
axes are drawn, the y-axis is displayed on the left (axes_visible=[«on» «on»];box=»off»,y_location=»left»). This is the default value.
The axes aspect can also be customized through the axes entity properties (see axes_properties).
More information
Enter the command plot2d() to see a demo.
Other high level plot2d functions exist:
plot2d2 same as plot2d but the curve is supposed to be piecewise constant.
plot2d3 same as plot2d but the curve is plotted with vertical bars.
plot2d4 same as plot2d but the curve is plotted with vertical arrows.
Построение графиков Scilab
Математический пакет Scilab располагает широким и гибко настраиваемым аппаратом для построения двумерных графиков и трёхмерных изображений.
Математический пакет Scilab располагает широким и гибко настраиваемым аппаратом для построения двумерных графиков и трёхмерных изображений.
Перечислим основные функции для оформления графика:
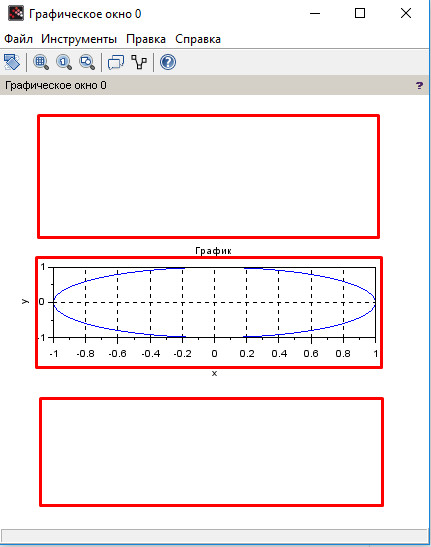
Например, subplot(312) разобъёт графичекое окно на 3 строки, 1 столбец и нарисует график во второй ячейке:
Расположение графика в графическом окне subplot(312).
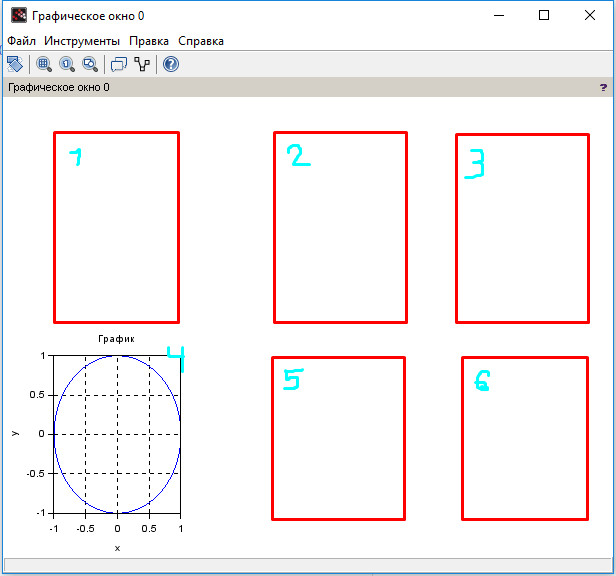
Например, subplot(234) разобъёт графичекое окно на 2 строки, 3 столбца и нарисует график в четвёртой ячейке:
Расположение графика в графическом окне subplot(234).
5.1 Двумерные графики
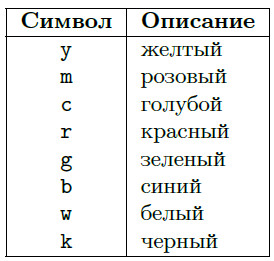
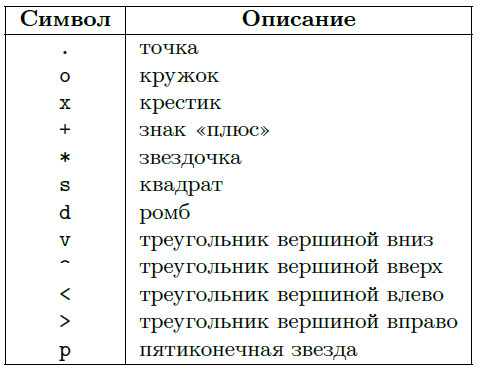
Установить желаемый вид и цвет графика можно, указав строковый параметр \( s \), который может состоять из одного, двух или трёх символов, определяющие соответственно: цвет линии, тип маркера, тип линии графика. Возможные значения перечислены в таблицах 2-4.
Таблица 2. Символы, определяющие цвет линии графика.
Таблица 3. Символы, определяющие тип линии графика.
Таблица 4. Символы, определяющие тип маркера
Для демонстрации работы функции plot() построим графики траектории движения точки по заданным уравнениям \( x(t), y(t) \) на плоскости и в заданном диапазоне времени T (таблица 5). Определим внешний вид каждого из графиков, а также оформим систему координат со всеми необходимыми подписями (листинг 13). Результат работы программы представлен на рис. 7.
Таблица 5. Уравнения движения материальной точки и промежуток времени.
Рисунок 7. Построение графиков движения материальной точки.
5.2 Построение трёхмерных изображений
Процесс построения графика функции вида \( Z(x,y) \) можно разделить на 3 этапа:
1. Создание прямоугольной сетки с помощью функции linspace();
2. Вычисление значений функции \( Z(x,y) \) в узлах сетки;
3. Вызов функции plot3d() или plot3d2().
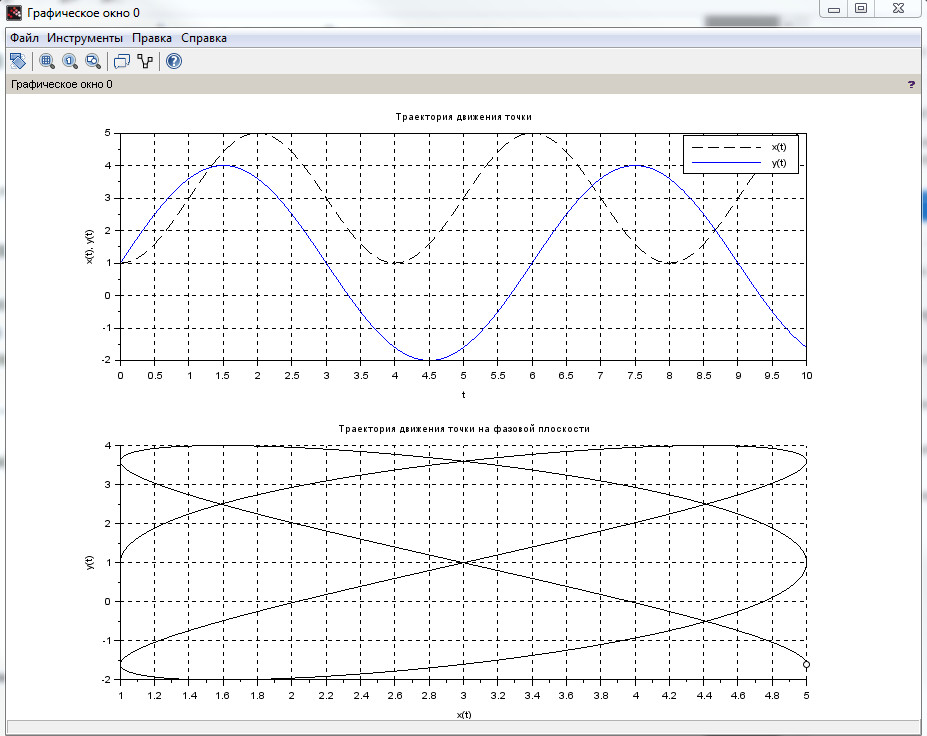
В качестве примера, построим сферу в трехмерной системе координат с помощью функций plot3d1 и plot3d2.
Рисунок 8. Сфера, заданная параметрически, построенная с помощью функции plot3d1 (слева) и plot3d2 (справа).
Поверхность сферы в декартовых координатах \( (x,y,z) \) параметрически задаётся системой уравнений: \( f(n) = \begin
независимые переменные \( u и v \) изменяются на промежутке \( [-\pi; \pi] \). Результат работы программы представлен на рис.8, исходный код на листинге 14.
Кроме того, если какая-либо функция из \( X, Y или Z\) зависит только от одного параметра \( u или v \), необходимо провести векторное умножение на единичный вектор ones() размерности, равной размерности параметра, от которого эта функция не зависит (см. строку 10 листинга 14).
plot2d
Calling Sequence
Arguments
a real matrix or vector. If omitted, it is assumed to be the vector 1:n where n is the number of curve points given by the y parameter.
a real matrix or vector.
sets the style for each curve. The associated value should be a real vector with integer (positive or negative) values.
controls the display of captions.
strf is a string of length 3 «xyz» (by default strf= «081» )
sets the curves captions. The associated value should be a character string.
sets the axes labels and tics definition. The associated value should be a real vector with four integer entries [nx,Nx,ny,Ny].
controls the computation of the actual coordinate ranges from the minimal requested values. The associated value should be an integer ranging from 0 to 8.
specifies how the axes are drawn. The associated value should be an integer ranging from 0 to 5.
Description
plot2d plots a set of 2D curves. If you are familiar with Matlab plot syntax, you should use plot.
The arguments should be used to customize the plot
This option may be used to specify how the curves are drawn. If this option is specified, the associated value should be a vector with as many entries as curves.
if style(i) is strictly positive, the curve is drawn as plain line and style(i) defines the index of the color used to draw the curve (see getcolor). Note that the line style and the thickness can be set through the polyline entity properties (see polyline_properties).
Piecewise linear interpolation is done between the given curve points.
if style(i) is negative or zero, the given curve points are drawn using marks, abs(style(i)) defines the mark with id used. Note that the marks color and marks sizes can be set through the polyline entity properties (see polyline_properties).
is a string of length 3 «xyz» (by default strf= «081» )
controls the display of captions.
controls the computation of the actual coordinate ranges from the minimal requested values. Actual ranges can be larger than minimal requirements.
no computation, the plot use the previus (or default) scale
from the min/max of the x, y datas
built for an isometric scale from the rect arg
built for an isometric plot from the min/max of the x, y datas
enlarged for pretty axes from the rect arg
enlarged for pretty axes from the min/max of the x, y datas
like y=1 but the previus plot(s) are redrawn to use the new scale
like y=2 but the previus plot(s) are redrawn to use the new scale
controls the display of information on the frame around the plot. If axes are requested, the number of tics can be specified by the nax optional argument.
nothing is drawn around the plot.
axes are drawn, the y=axis is displayed on the left.
the plot is surrounded by a box without tics.
axes are drawn, the y=axis is displayed on the right.
axes are drawn centred in the middle of the frame box.
The curve captions are drawn on below the x-axis. This option is not flexible enough, use the captions or legend functions preferably.
This option may be used to set the mimimal bounds requested for the plot. If this option is specified, the associated value should be a real vector with four entries:
The axes boundaries can also be customized through the axes entity properties (see axes_properties).
Ny and ny give similar information for the y-axis.
If axesflag option is not set nax option supposes that axesflag option has been set to 9.
This option may be used to control the computation of the actual coordinate ranges from the minimal requested values. Actual ranges can be larger than minimal requirements.
no computation, the plot use the previous (or default) scale.
The actual range is the range given by the rect option.
The actual range is computed from the min/max of the x and y data.
The actual range is the range given by the rect option and enlarged to get an isometric scale.
The actual range is computed from the min/max of the x and y data and enlarged to get an isometric scale.
The actual range is the range given by the rect option and enlarged to get pretty axes labels.
The actual range is computed from the min/max of the x and y data and enlarged to get pretty axes labels.
like frameflag=1 but the previous plot(s) are redrawn to use the new scale. Used to add the current graph to a previous one.
like frameflag=2 but the previous plot(s) are redrawn to use the new scale. Used to add the current graph to a previous one.
like frameflag=8 but the range is enlarged to get pretty axes labels. This is the default value.
The axes boundaries can also be customized through the axes entity properties (see axes_properties)
This option may be used to specify how the axes are drawn. The associated value should be an integer ranging from 0 to 5 :
nothing is drawn around the plot (axes_visible=[«off» «off»];box=»off»).
axes are drawn, the y-axis is displayed on the left (axes_visible=[«on» «on»];box=»on»,y_location=»left»).
the plot is surrounded by a box without tics (axes_visible=[«off» «off»];box=»on»).
axes are drawn, the y-axis is displayed on the right (axes_visible=[«on» «on»];box=»off»,y_location=»right»).
axes are drawn centered in the middle of the frame, the box being not drawn (axes_visible=[«on» «on»];box=»off»,x_location=»middle», y_location=»middle»).
axes are drawn, the y-axis is displayed on the left (axes_visible=[«on» «on»];box=»off»,y_location=»left»). This is the default value
The axes aspect can also be customized through the axes entity properties (see axes_properties).
More information
Enter the command plot2d() to see a demo.
Other high level plot2d functions exist:
plot2d2 same as plot2d but the curve is supposed to be piecewise constant.
plot2d3 same as plot2d but the curve is plotted with vertical bars.
plot2d4 same as plot2d but the curve is plotted with vertical arrows.
Scilab/Графики
Во время работы в Scilab, представлять результаты в виде графиков приходится также часто, как и писать сценарии. В этой главе мы рассмотрим способы построения разных видов графиков.
Содержание
Основные понятия [ править ]
Для начала определим то, с чем мы будем иметь дело. График — это графическое представление функции. В среде Scilab все графики строятся по точкам, при этом каждые две соседние точки соединяются друг с другом отрезком. Чем меньше расстояние между точками, тем меньше искажение графика за счет замены его реального образа кусочно-линейной функцией. К сожалению, координаты точек нужно где-то хранить, что является главным ограничивающим фактором в желании получить как можно более плавное представление.
Внешний вид графика определяют следующие факторы:
Все графики в Scilab строятся в так называемых графических окнах (англ. Figure ). Графические окна используются не только для построения графиков, но и для создания пользовательских интерфейсов, анимации и рисования, о чем подробнее будет рассказано в другом разделе. Каждое графическое окно имеет идентификатор, который называется дескриптором графического окна или просто дескриптором (англ. Handle ), когда опускание уточнения не вводит в заблуждение. В дальнейшем вы увидите, что дескриптор есть не только у графических окон.
Любое графическое окно в Scilab это отдельный объект, обладающий широким набором параметров, отвечающих за его внешний вид. При построении графиков пользователь неявно обращается к рабочей области графического окна, когда, например, чертит оси, сетку, отмечает точки и соединяет их прямыми. Построение графика на самом деле сложный процесс, связанный с рисованием линий на мониторе. К счастью для построения графиков в системе есть множество предопределенных функций, которые выполняют всю построительную работу в графическом окне. От пользователя лишь требуется знания всех этих функций и правил их применения.
Далее, говоря слово график, мы будем понимать график функции вместе со всеми дополнительными элементами, как оси, сетка подписи и т.п.
Создание графического окна [ править ]
Для того, чтобы создать графическое окно необходимо воспользоваться функцией
Данная функция ожидает в качестве аргумента целое число, которое будет определять номер окна в системе. Если пользователь ничего не передаст, то система присвоит окну последний не занятый порядковый номер, начиная с нуля. В ответ данная функция возвращает дескриптор окна, а также набор его параметров. Большая часть параметров заранее предопределена.
Давайте попробуем создать графическое окно
После вызова функции появится графическое окно с номером 0, а в командном окне вы увидите параметры данного окна.
Белая область графического окна, которую вы видите, называется рабочей и вы вольны рисовать на ней все, что вам захочется, в том числе и графики.
Давайте создадим еще одно графическое окно, но определим его номер самостоятельно. Для этого введем команду
Теперь у нас два графических окна под номерами 0 и 5, текущим из которых является окно 5. Чтобы посмотреть весь перечень открытых окон, необходимо вызвать макрос
который вернет вектор с номерами всех открытых графических окон. Давайте снова сделаем активным окно 0, для чего вызовем функцию scf()
Закрыть графическое окно можно двумя способами:
Последний способ обычно применяется в сценариях, когда управление окнами осуществляется программно. Закроем окно 5 и убедимся, что оно закрылось
Мы пока отвлечемся от настройки графических окон и перейдем непосредственно к построению графиков. Отметим также, что если за время сеанса не было создано ни одного графического окна, то функции рисования создают его автоматически. В любом случае, если вы желаете полностью управлять всем процессом, то рекомендуется создавать окна вручную.
Построение графиков [ править ]
Любой график имеет следующие элементы:
При вызове непосредственно функций построения, многие второстепенные элементы строятся автоматически по заранее заготовленным шаблонам, однако, всеми этими элементами можно управлять.
Построение графиков одномерных функций [ править ]
Как было сказано ранее, все графики строятся по точкам, а сам массив точек иногда называют точечной функцией. У одномерной функции точка характеризуется двумя координатами — значением аргумента и значением функции. Обычно множество значений аргумента и функции записываются в векторы, которые передаются уже в качестве аргументов для строящих функций.
Для построения одномерных функций в прямоугольной системе координат служат следующие функции:
Для начала попробуем построить параболу через точечную функцию. Для этого определим квадратичную функцию
Самый простой вызов функции plot2d() заключается в передаче именно этих векторов в качестве аргументов. Если до этого ни одного графического окна не было создано, то оно будет создано автоматически. Вызовите функцию
Вы увидите самый простой график, на котором будут нарисованы две оси с подобранным масштабом. Сам график будет черного цвета. Все остальные элементы графика считаются опциональными и могут быть включены различными способами.
Давайте построим второй график на той же плоскости и множестве аргументов, но введем уже другую функцию, например, кубическую. Вы можете не объявлять функцию отдельно и не заготавливать точки, а передать в качестве аргумента алгебраическое выражение. В этом случае вектор значений функций до построения будет приготовлен за вас на основе тех значений аргумента, которые вы передали.
При таком способе вызова множество значений функции было рассчитано автоматически. Сам график кубической параболы был построен поверх и также черным цветом. Обратите внимание, что масштаб осей изменился так, чтобы было видно точки обеих функций. Множество точек на экране ограниченных квадратом, в который помещаются все точки всех графиков, образует особую область, которую можно масштабировать, уменьшать и увеличивать так, как это нужно пользователю.
Сделайте активным графическое окно. Затем попробуйте покрутить колесико мыши. Таким образом, вы можете управлять масштабом в пределах множества определенных заранее аргументов. Если вы зажмете левую кнопку мыши и попробуете перетащить курсор, то увидите как передвигается область. При этом оси перестраиваются автоматически.
График в графическом окне также является объектом и может быть стерт. Этот процесс может показаться сложным, но на начальном этапе попробуем показать всю суть объектно-ориентированной парадигмы.
Рисование графика — сложный процесс, который заключается в создании объектов в понимании объектно-ориентированного программирования. Например, сначала было создано графическое окно «Figure» (объект), которое затем породило потомков (англ. Children ) «Axes» (оси, которые вы видите на экране). У осей тоже есть потомки и это как раз сами линии графика, которые к ним привязываются.
Любой объект в Scilab является типизованным списком, указатель на который мы и называем дескриптором. Для извлечения параметров графических объектов служит функция get(). Для примера, давайте посмотрим сколько потомков у наших осей
В данном примере функция вернула дескриптор осей текущего графического окна с полным перечнем свойств. Мы можем наблюдать, что оси текущего графического окна имеют два потомка, отраженных в строке children. Чтобы удалить потомков, а следовательно стереть график, необходимо воспользоваться функцией delete(). Давайте удалим график параболы, для чего нужно просто правильно передать дескриптор интересующего нас объекта.
Обратите внимание на то, что дескриптор потомка-параболы имеет индекс 2, так как каждый новый созданный объект занимает позицию (1), тем самым смещая все остальные вверх. Если все сделано правильно, то вы увидите, что график параболы пропал. Если вы обратитесь снова к списку потомков, то увидите, что удаление прошло успешно
Из этого примера, вы должны вынести то, что для успешной работы с внутренними объектами среды достаточно знать их устройство и функции-примитивы (называемые также методами), работающие с этими объектами.
Теперь предлагаем читателю самостоятельно построить график с помощью функции fplot2d(). Напомним, что ей не нужны сами координаты, а нужна формула, по которой значения функции будут рассчитаны. Это удобно, когда вы работаете не с экспериментальными данными, где обычно имеют дело с точечными функциями, а с аналитически определенными функциями. Чтобы функция fplot2d() сработала, ей нужно передать два аргумента: вектор значений аргумента и имя заранее определенной функции (без аргументов).
В рамках данного упражнения, выполните следующие шаги:
Для построения графиков в полярной системе координат служит функция polarplot(). Полный прототип функции выглядит так
Очевидно, что самый простой вызов этой функции схож с вызовом plot2d, а разница лишь в том, как определяется координата каждой следующей точки. Настройка внешнего вида графиков для всего семейства функций-построителей одномерных функций в целом одинаковая, поэтому основные принципы мы рассмотрим ниже.
Построения функций в комплексной плоскости по смыслу похожи на построение в прямоугольной системе координат, где по оси абсцисс отсчитывается действительная часть функции, а по оси ординат — мнимая. Для некоторых частных примеров существуют готовые функции-построители. Некоторые из них(например, построение годографа Найквиста) мы рассмотрим чуть позже.
Опираясь на предыдущий материал самостоятельно постройте графики показанные на рисунке.
Двумерное построение графиков [ править ]
В предыдущих упражнениях мы показали, что по внутренней организации график является объектом (в понимании объектно-ориентированной парадигмы), а точнее говоря существует предопределенный класс, который является формой для создания графиков как объектов. Вы могли видеть полный перечень параметров этого класса, которые определяют поведение конкретного экземпляра этого класса (или того, что мы называем объектом). Также один объект может порождать потомков — экземпляры подмножества классов, для которых данный класс является родительским. Таким образом, зная назначения тех или иных параметров, вы можете полностью управлять объектом как вам нужно. Однако, вы наверное заметили как этих параметров много, а держать их в голове становится не практичным.
К счастью, ручное редактирование параметров в большинстве случаев не нужно, потому что часть параметров заложено в функции-построители, а внешний вид самого графика может быть изменен через встроенный редактор. Кроме того, многие функции для построения графиков имеют похожие прототипы и разница зачастую обусловлена только системой координат.
Полный прототип функции plot2d() имеет следующий вид (квадратные скобки означают необязательные аргументы или флаги)
Здесь мы отметим, что некоторые параметры имеют большое количество возможных значений, что порождает еще большее количество возможных комбинаций. Обычное их перечисление здесь не поспособствует быстрого освоения ими, поэтому мы рекомендуем вам поэкспериментировать самостоятельно со всеми этими параметрами. Для начала мы приведем несколько поучительных примеров. Возможные значения этих параметров мы специально вынесли в приложение к учебнику. Также вы всегда можете воспользоваться справкой Scilab, воспользовавшись командой help.
Пример 1
Постройте график функции синуса в диапазоне от 1 до 4π со следующими параметрами:
Если все сделано правильно, то вы должны увидеть результат показанный на рисунке. Обратите внимание на то, что у осей два потомка: график и легенда. Именно поэтому при обращении к потомкам осей мы указали индекс, указывающий на график. Функция color() возвращает внутренний код цвета по его имени или RGB коду (color(r,g,b)). Никакой ошибки не будет, если ввести код сразу, например, для синего это 2.
На «своей шкуре» вы только что почувствовали как это трудоемко производить настройку вручную. К счастью, разработчики подумали о пользователе и внедрили в среду графический редактор (англ. Graphic Editor ), который сам обращается ко всем параметрам. Пользователю же нужно просто правильно выбрать параметр и ввести в поле значение. Окно редактора строится также как и любое графическое окно с помощью интерфейса Tcl/Tk. Данный интерфейс поддерживается только в версиях для Windows и Unix-подобных систем, т.е. пользователи Mac OS не смогут воспользоваться редактором. В будущей версии 6 разработчики обещали исправить это недоразумение.
Чтобы открыть редактор нужно:
После этого откроется окно редактора в котором вы увидите слева дерево объектов данного графического окна. Переключаясь по пунктам этого дерева вы будете видеть справа параметры этого окна. Некоторые из них вводятся в поля, некоторые переключаются с помощью ползунков, а некоторые имеют раскрывающееся меню. Если вы не знаете, что делает тот или иной параметр, вы можете поэкспериментировать, так как результат меняется на ваших глазах. Следует помнить, что подписи в окне могут не соответствовать истинным названиям параметров в самом типизованном списке класса.
Действия над графиками [ править ]
Как вы уже знаете, все функции-построители, вызванные в командном окне, будут рисовать в текущем графическом окне. Это означает, что все объекты, которые будут ими создаваться, будут накладываться поверх уже созданных. Для удаления объектов в графическом окне служит функция delete(), однако, если вы хотите очистить графическое окно сразу, проще воспользоваться функцией
Для получения дескрипторов различных графических объектов существует универсальная функция get(), а также несколько макросов на нее.
Если вы помните номер графического окна, то получить его дескриптор можно с помощью функции
Для установки значения параметра объекта вы, как мы это делали раньше, можете обратиться к параметру, как к полю типизованного списка, однако, есть еще специальная для этого функция set(). Преимущество функции перед простым обращением состоит в том, что вы можете использовать для получения дескрипторов макросы функции get() и не хранить дескрипторы в отдельных переменных.
Управление дескрипторами возможно через функции, реализующие следующие операции:
Управлять графиками можно также с помощью мыши и инструментов графического окна. Все необходимые функции дублируются в раскрывающемся и контекстном меню. Например, чтобы очистить графическое окно, достаточно сделать активным, а затем в раскрывающемся меню Правка выбрать пункт Очистить графическое окно. Кроме того, вы также можете выделять построенные объекты и нажимая правой кнопкой мыши на них, вызывать контекстное меню, в котором доступны такие команды как Удалить, Копировать, Вставить и др. Все эти возможности на самом деле неявный вызов встроенных функций, позволяющие уменьшить количество рутинной работы. Однако, вам не стоит расслабляться по этому поводу, ведь без умения работать с этими функциями из командной строки или сценария, вы не сможете полноценно работать в среде.
Вы увидите два графика. Для построения, первым вызовом функции xsetech() мы передали позицию (в относительных единицах) на которой будет размещен верхний график. Первые два числа означают позицию верхнего левого угла подокна. Вторые два числа означают длину и высоту в относительных единицах, т.е. 1 означает, что подокно должно растянуться по всей длине, 0.5 — растягивание на половину высоты всего графического окна. Второй вызов xsetech() аналогичен первому, за исключением того, что верхний левый угол второго подокна должен занять позицию на половине высоты всего графического окна.
Очевидно, что полярный график занимает меньше места и плохо просматривается, поэтому давайте перенесем его на другое окно. Операция переноса складывается из трех более мелких: копирование дескриптора осей, регистрация скопированного дескриптора как потомка нового графического окна, удаление дескриптора осей из старого окна. Для примера, провернем эту операцию вручную, через командную строку.
Обратите внимание, что функции copy() мы первым аргументом передали источник, а вторым — место назначение. Сделав видимым окно 1, вы увидите, что график был скопирован с тем же форматированием и занимает ровно нижнюю половину окна, что не являлось первоначальной задумкой. Вообще говоря, функция скопировала разбивку окна 0 целиком, просто не скопировала наш график параболы. Давайте поправим внешний вид графика.
Теперь нарисуем в графическом окне 0 еще один график
Новый график был построен на осях, созданных автоматически с графическим окном, однако на него визуально накладывается график параболы, который существует в подокне. При этом в дереве объектов графического окна график кубической параболы лежит как бы на фоновом слое, а график параболы на внешнем слое. Введите следующие команды
После ввода второй инструкции выделите графическое окно 0 и вы увидите, как два графика поменялись местами: теперь график кубической параболы накладывается поверх графика параболы. Все дело в том, что мы поменяли дескрипторы осей местами, а графическая отрисовка потомков происходит послойно так, что потомок с меньшим индексом оказывается сверху. Так как фоны обоих графиков не являются прозрачными (а это можно всегда настроить), они и перекрывают друг друга.
Вы уже знаете, что за масштабирование осей отвечает параметр axes_bounds. Настроим график кубической параболы.
Хотя формально слой с кубической параболой никуда не делся, мы настроили параметр отрисовки осей так, чтобы они не пересекались с верхним графиком.
Наконец, продемонстрируем функцию glue(), название которой переводится как «клей», что намекает на ее назначение. Склеим оба графика.
Теперь оба графика формально имеют один дескриптор. Применительно к графикам такая группировка редко бывает полезной, так как из-за нее блокируются некоторые операции. Обычно склеивание используется в программируемом рисовании.
Построение графиков трехмерных функций [ править ]
Каждая точка графика трехмерной функции имеет три координаты, одна из которых обычно является функцией от оставшихся двух. Множество этих точек образует поверхность.
В целом построение поверхностей мало отличается от построения графиков одномерных функций и все, что было рассказано ранее, применимо и здесь. Разница главным образом заключается в структуре типизованного списка, в котором добавляется дополнительная ось OZ.
Поверхности строятся следующими функциями: