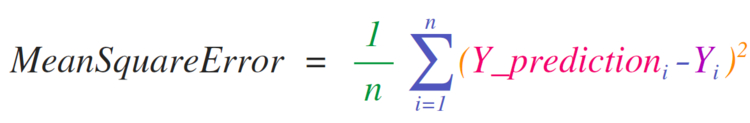numpy dot что это
Функция numpy.dot() в Python
Чтобы вычислить скалярное произведение массивов numpy nd, вы можете использовать функцию numpy.dot() в Python. Она принимает в качестве аргументов два массива numpy, вычисляет их скалярное произведение и возвращает результат.
Синтаксис
Синтаксис метода numpy.dot():
| Параметр | Описание |
|---|---|
| a | [обязательный] Первый аргумент для операции скалярного произведения. |
| b | [обязательный] Второй аргумент для операции скалярного произведения. |
| out | [необязательно] Этот аргумент используется для оценки производительности. Это должен быть C-смежный массив, а dtype должен быть тем dtype, который будет возвращен для точки (a, b). |
На основе размеров входного массива
В следующей таблице указывается тип выполняемой операции на основе размеров входных массивов: a и b.
| Размерности «a» и «b» | Выход |
|---|---|
| Нулевое измерение (скалярное) | Умножение двух скаляров a и b. |
| Одномерные массивы (вектор) | Внутреннее произведение векторов. |
| Двумерные массивы (матрица) | Умножение матриц. |
| a: N-мерный массив, b: 1-мерный массив | Суммируйте произведение по последней оси a и b. |
| a: N-мерный массив, b: M-мерный массив (M> = 2) | Суммируйте произведение по последней оси a и предпоследней оси b. |
Пример 1: произведение скаляров с несколькими точками
В этом примере мы берем два скаляра и вычисляем их скалярное произведение с помощью функции numpy.dot(). Точечное произведение с двумя скалярами в качестве аргументов возвращает умножение двух скаляров.
Пример 2: произведение числовых точек одномерных массивов
В этом примере мы берем два numpy одномерных массива и вычисляем их скалярное произведение с помощью функции numpy.dot(). Мы уже знаем, что если входные аргументы метода dot() одномерные, то выход будет внутренним произведением этих двух векторов (поскольку это одномерные массивы).
Пример 3: произведение числовых точек двумерных массивов
В этом примере мы берем два двумерных массива numpy и вычисляем их скалярное произведение. Точечное произведение двух двумерных массивов возвращает матричное умножение двух входных массивов.
В этом руководстве на примерах Python мы узнали, как вычислить скалярное произведение массивов numpy с помощью примеров программ.
numpy.dot¶
Dot product of two arrays. Specifically,
If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).
If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.
If either a or b is 0-D (scalar), it is equivalent to multiply and using numpy.multiply(a, b) or a * b is preferred.
If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.
If a is an N-D array and b is an M-D array (where M>=2 ), it is a sum product over the last axis of a and the second-to-last axis of b:
b array_like
out ndarray, optional
Output argument. This must have the exact kind that would be returned if it was not used. In particular, it must have the right type, must be C-contiguous, and its dtype must be the dtype that would be returned for dot(a,b). This is a performance feature. Therefore, if these conditions are not met, an exception is raised, instead of attempting to be flexible.
Returns output ndarray
Returns the dot product of a and b. If a and b are both scalars or both 1-D arrays then a scalar is returned; otherwise an array is returned. If out is given, then it is returned.
If the last dimension of a is not the same size as the second-to-last dimension of b.
Numpy Dot Product в Python С примерами
Примеры и объяснения numpy dot product в python для скаляров, комплексных векторов, одномерных и двумерных массивов.
Numpy Dot Product в Python С примерами
Здравствуйте программисты, в этой статье мы обсудим продукты Numpy dot в Python. Функция Numpy dot() вычисляет точечное произведение Numpy n-мерных массивов. Функция numpy.dot () принимает два массива numpy в качестве аргументов, вычисляет их точечное произведение и возвращает результат.
Для 1D массивов это внутреннее произведение векторов. Он выполняет точечное произведение над 2-D массивами, рассматривая их как матрицы. Следовательно, выполнение матричного умножения над ними. Мы рассмотрим реализацию функции numpy.dot() над скалярами, векторами, массивами и матрицами. Перед этим позвольте мне просто кратко рассказать вам о синтаксисе и типе возвращаемого значения продукта Numpy dot в Python.
Синтаксис функции numpy dot()
Параметры:
Возвращаемый тип функции Numpy Dot()
Скалярное Числовое точечное произведение
Объяснение:
В приведенном выше примере два скалярных числа передаются в качестве аргумента функции np.dot (). Таким образом, эта функция numpy dot вычисляет точечное произведение двух скаляров путем вычисления их умножения. Передача и в np.dot() возвращает 18.
Numpy dot произведение комплексных векторов
Объяснение:
В приведенном выше примере функция numpy dot находит точечное произведение двух комплексных векторов. Поскольку vector_a и vector_b являются комплексными, для этого требуется комплексное сопряжение любого из двух комплексных векторов.
Здесь используется комплексное сопряжение vector_b, т. е. (5 + 4j) и (5 _ 4j).
Функция np.dot() вычисляет точечное произведение как: 2(5 + 4j) + 3j(5 – 4j)
Таким образом, передавая vector_a и vector_b в качестве аргументов функции np.dot (), она возвращает (-2 + 23j) в качестве выходных данных.
Numpy dot произведение 1D массивов
Во-первых, два массива инициализируются путем передачи значений в метод np.array() для A и B. Созданные A и B представляют собой одномерные массивы. Функция numpy dot вычисляет точечное произведение для этих двух 1D массивов следующим образом:
в качестве выходных данных возвращается скалярное значение 77.
Точечное произведение над 2D массивами
Объяснение:
метод np.array() инициализирует два массива A и B. Созданные A и B представляют собой двумерные массивы. Точечное произведение двух 2-D массивов возвращается как матричное умножение этих двух входных массивов. Точечный продукт для href=”https://en.wikipedia.org/wiki/3D”>3D массивы вычисляются как: href=”https://en.wikipedia.org/wiki/3D”>3D массивы вычисляются как:
Таким образом, передавая 2D-массивы A и B в функцию np.dot (), результирующий вывод также является 2D-массивом.
Далее объясняется в Python Vectors, что все операции предварительно встроены в numpy, включая точечный продукт.
Вывод
В этой статье мы узнали, как найти точечное произведение двух скаляров и комплексных векторов. Мы также изучили работу функции Numpy dot на 1D и 2D массивах с подробными примерами. Обратитесь к этой статье для любых запросов, связанных с продуктом Numpy dot в Python.
Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.
numpy.dot¶
Dot product of two arrays. Specifically,
If both a and b are 1-D arrays, it is inner product of vectors (without complex conjugation).
If both a and b are 2-D arrays, it is matrix multiplication, but using matmul or a @ b is preferred.
If either a or b is 0-D (scalar), it is equivalent to multiply and using numpy.multiply(a, b) or a * b is preferred.
If a is an N-D array and b is a 1-D array, it is a sum product over the last axis of a and b.
If a is an N-D array and b is an M-D array (where M>=2 ), it is a sum product over the last axis of a and the second-to-last axis of b:
b array_like
out ndarray, optional
Output argument. This must have the exact kind that would be returned if it was not used. In particular, it must have the right type, must be C-contiguous, and its dtype must be the dtype that would be returned for dot(a,b). This is a performance feature. Therefore, if these conditions are not met, an exception is raised, instead of attempting to be flexible.
Returns output ndarray
Returns the dot product of a and b. If a and b are both scalars or both 1-D arrays then a scalar is returned; otherwise an array is returned. If out is given, then it is returned.
If the last dimension of a is not the same size as the second-to-last dimension of b.
Изучение NumPy с визуальными примерами для начинающих
Пакет NumPy является незаменимым помощником Python. Он тянет на себе анализ данных, машинное обучение и научные вычисления, а также существенно облегчает обработку векторов и матриц. Некоторые ведущие пакеты Python используют NumPy как основной элемент своей инфраструктуры. К их числу относятся scikit-learn, SciPy, pandas и tensorflow. Помимо возможности разобрать по косточкам числовые данные, умение работать с NumPy дает значительное преимущество при отладке более сложных сценариев библиотек.
Содержание
В данной статье будут рассмотрены основные способы использования NumPy на примерах, а также типы представления данных (таблицы, картинки, текст и так далее) перед их последующей подачей модели машинного обучения.
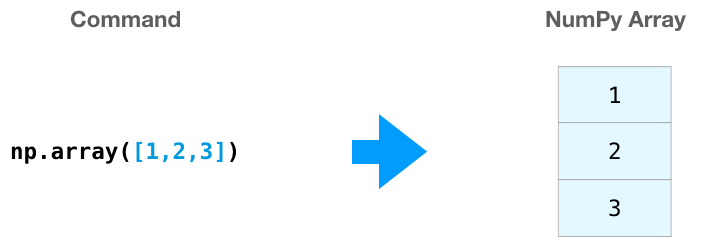
Создание массивов NumPy
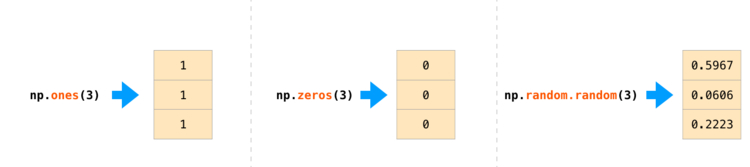
Нередки случаи, когда необходимо, чтобы NumPy инициализировал значения массива.
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
После создания массивов можно манипулировать ими довольно любопытными способами.
Арифметические операции над массивами NumPy
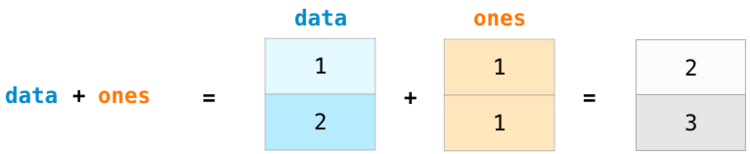
Создадим два массива NumPy и продемонстрируем выгоду их использования.
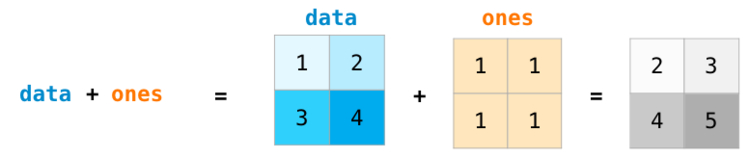
Массивы будут называться data и ones :
При сложении массивов складываются значения каждого ряда. Это сделать очень просто, достаточно написать data + ones :
Новичкам может прийтись по душе тот факт, что использование абстракций подобного рода не требует написания циклов for с вычислениями. Это отличная абстракция, которая позволяет оценить поставленную задачу на более высоком уровне.
Помимо сложения, здесь также можно выполнить следующие простые арифметические операции:
Как можно увидеть в примере выше, NumPy сам понял, что умножить на указанное число нужно каждый элемент массива. Данный концепт называется трансляцией, или broadcating. Трансляция бывает весьма полезна.
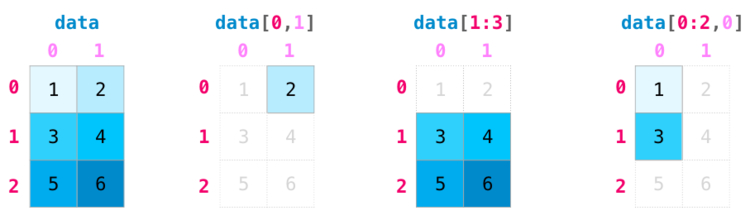
Индексация массива NumPy
Массив NumPy можно разделить на части и присвоить им индексы. Принцип работы похож на то, как это происходит со списками Python.
Агрегирование в NumPy
Дополнительным преимуществом NumPy является наличие в нем функций агрегирования:
Это лишь небольшая часть довольно обширного списка функций агрегирования в NumPy.
Использование нескольких размерностей NumPy
Создание матриц NumPy на примерах
Созданные в следующей форме списки из списков Python можно передать NumPy. Он создаст матрицу, которая будет представлять данные списки:
Достаточно только добавить им кортеж, в котором будут указаны размерности матрицы, которую мы создаем.
Арифметические операции над матрицами NumPy
Арифметические операции над матрицами разных размеров возможны в том случае, если размерность одной из матриц равно одному. Это значит, что в матрице только один столбец или один ряд. В таком случае для выполнения операции NumPy будет использовать правила трансляции:
dot() Скалярное произведение NumPy
На изображении выше под каждой фигурой указана ее размерность. Это сделано с целью отметить, что размерности обеих матриц должны совпадать с той стороны, где они соприкасаются. Визуально представить данную операцию можно следующим образом:
Индексация матрицы NumPy
Операции индексации и деления незаменимы, когда дело доходит до манипуляции с матрицами:
Агрегирование матриц NumPy
Агрегирование матриц происходит точно так же, как агрегирование векторов:
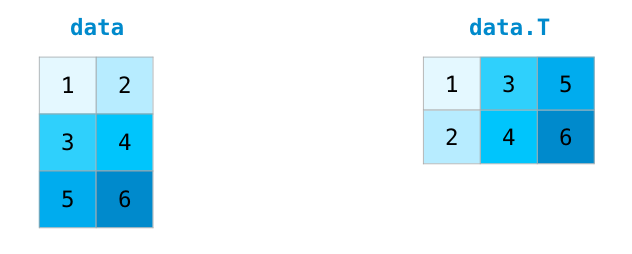
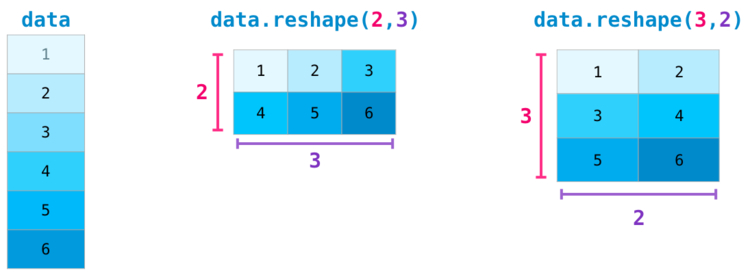
Транспонирование и изменение формы матриц в numpy
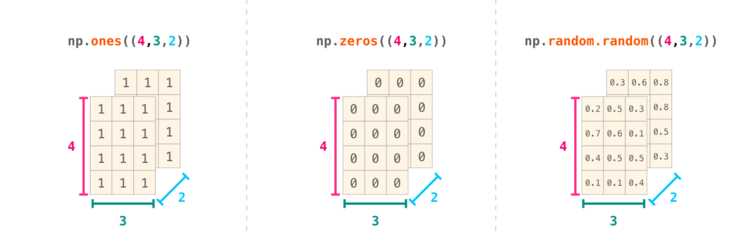
Еще больше размерностей NumPy
В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:
На заметку: Стоит иметь в виду, что при выводе 3-мерного массива NumPy результат, представленный в виде текста, выглядит иначе, нежели показано в примере выше. Порядок вывода n-мерного массива NumPy следующий — последняя ось зацикливается быстрее всего, а первая медленнее всего. Это значит, что вывод np.ones((4,3,2)) будет иметь вид:
Примеры работы с NumPy
Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.
Математические формулы NumPy
Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу среднеквадратичной ошибки, которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:
Реализовать данную формулу в NumPy довольно легко:
Главное достоинство NumPy в том, что его не заботит, если predictions и labels содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:
У обоих векторов predictions и labels по три значения. Это значит, что в данном случае n равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:
Затем мы можем возвести значения вектора в квадрат:
Теперь мы вычисляем эти значения:
Таким образом мы получаем значение ошибки некого прогноза и score за качество модели.
Представление данных NumPy
Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:
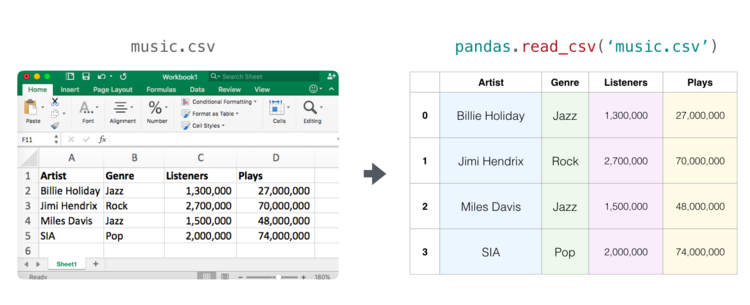
Таблицы NumPy — примеры использования таблиц
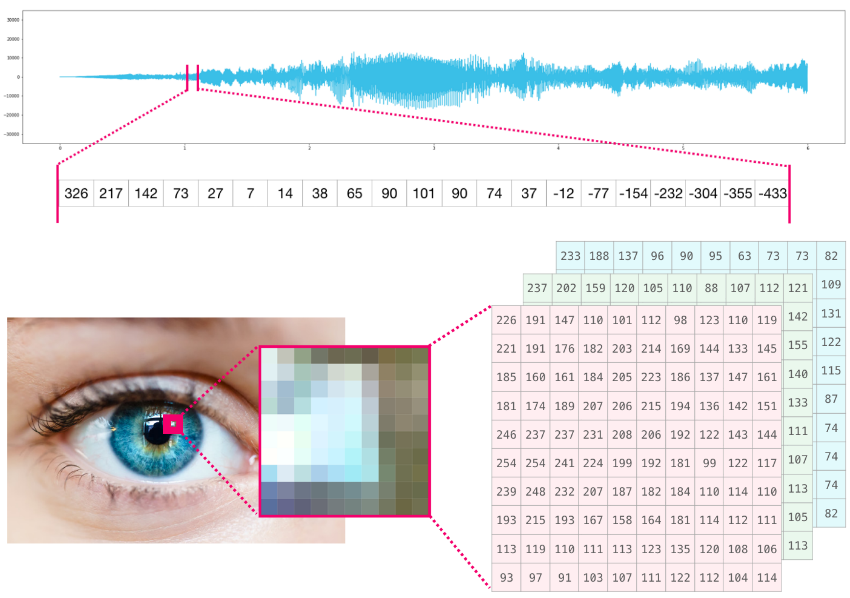
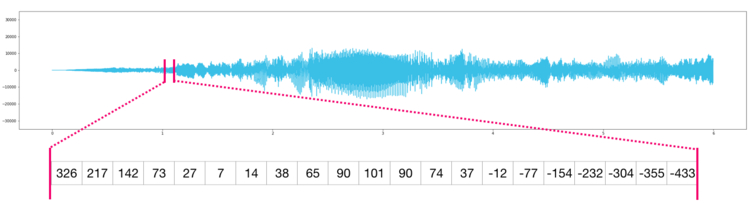
Аудио и временные ряды в NumPy
Фрагмент аудио файла выглядит следующим образом:
То же самое касается данных временных рядов, например, изменения стоимости акций со временем.
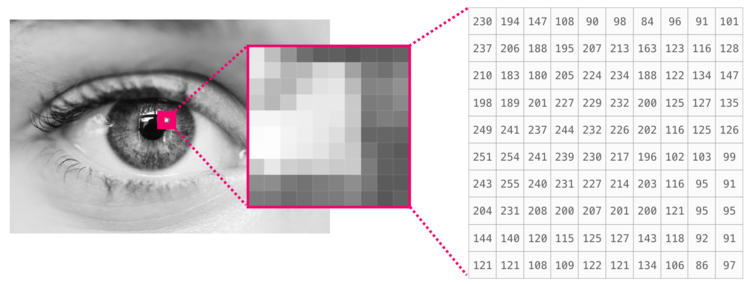
Обработка изображений в NumPy
Изображение является матрицей пикселей по размеру (высота х ширина).
Вот как выглядит фрагмент изображения:
Если изображение цветное, каждый пиксель представлен тремя числами. Здесь за основу берется цветовая модель RGB — красный (R), зеленый (G) и синий (B).
В данном случае нам понадобится третья размерность, так как каждая клетка вмещает только одно число. Таким образом, цветная картинка будет представлена массивом ndarray с размерностями: (высота х ширина х 3).
Обработка текста в NumPy на примерах
Когда дело доходит до текста, подход несколько меняется. Цифровое представление текста предполагает создание некого python словаря, то есть инвентаря всех уникальных слов, которые бы распознавались моделью, а также векторно (embedding step). Попробуем представить в цифровой форме цитату из стихотворения арабского поэта Антара ибн Шаддада, переведенную на английский язык:
“Have the bards who preceded me left any theme unsung?”
Перед переводом данного предложения в нужную цифровую форму модель должна будет проанализировать огромное количество текста. Здесь можно обработать небольшой набор данный, после чего использовать его для создания словаря из 71 290 слов.
Предложение может быть разбито на массив токенов, что будут словами или частями слов в зависимости от установленных общих правил:
Затем в данной таблице словаря вместо каждого слова мы ставим его id :
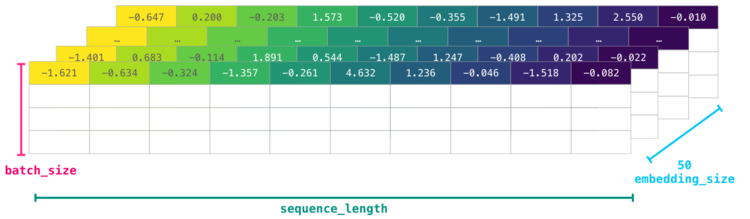
Однако данные id все еще не обладают достаточным количеством информации о модели как таковой. Поэтому перед передачей последовательности слов в модель токены/слова должны быть заменены их векторными представлениями. В данном случае используется 50-мерное векторное представление Word2vec.
Теперь мы получили числовой том, с которым модель может работать и делать полезные вещи. Некоторые строки остались пустыми, однако они могут быть заполнены другими примерами, на которых модель может тренироваться или делать прогнозы.
(На заметку: Поэма, строчку из которой мы использовали в примере, увековечила своего автора в веках. Будучи незаконнорожденным сыном главы племени от рабыни, Антара ибн Шаддан мастерски владел языком поэзии. Вокруг исторической фигуры поэта сложились мифы и легенды, а его стихи стали частью классической арабской литературы).
Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)