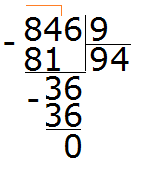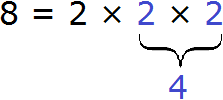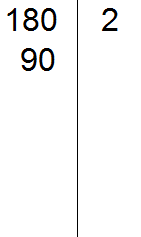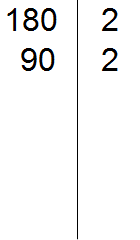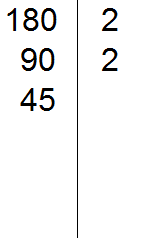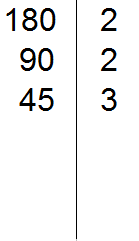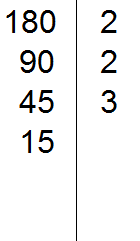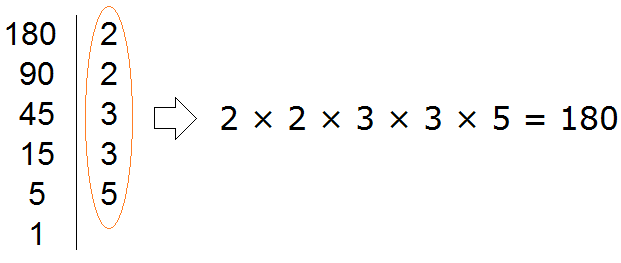Что значит простые делители

Делитель

Всего получено оценок: 331.

Всего получено оценок: 331.

Операция деления – это основа основ современного мира. Имеется в виду не только математика, но и все точные науки, биология, информатика и экономика. Поговорим об определении делителя числа в операции деления.

Что такое деление?

Деление это математическая операция второй ступени. Иногда ее еще называют второй степенью сложности. На первой ступени находятся сложение и умножение, на третьей возведение в степень и извлечение корня, на четвертой логарифмирование и так далее.

В теории сложность математических действий не ограниченна, по мере требований науки и техники будут возникать все новые и новые действия с числами. На сегодняшний день наиболее сложным вычислением считается дифференциация и извлечение интеграла.

Классическая формула деления выглядит так:

с-частное, то есть результат деления.

Самые простые операции деления можно проводить с помощью таблицы умножения. Например, если 3*5=15, то если число 15 поделить на 5 получится 3 и так далее.

Простые и сложные делители

Делители могут быть простыми и сложными или составными. Разберемся, что это значит. Простым делитель называют тогда, когда в качестве делителя выступает простое число. Соответственно сложный делитель – сложное или составное число.

Простым числом называют число, которое может делиться только на 1 и на себя. Такими числами являются 2,3, 5 и так далее. Чтобы не ошибиться, лучше использовать таблицу простых чисел. Любое число, которое не является простым, считается составным.

Простые делители в примерах и задачах встречаются редко. Просто потому, что выполнять действия с ними проще, а задача составителей учебников наоборот максимально усложнить задачу ученика.

Но простые делители нужны, когда число раскладывается на простые множители. Это нужно для того, чтобы определить наибольший общий делитель и наименьшее общее кратное числа. А НОК и НОД в свою очередь нужны для того, чтобы правильно складывать, вычитать и сравнивать дроби.

Правило знаков

От делителя так же зависит и знак частного, то есть результата деления. Все определяется правилом знаков:

Что мы узнали?

Мы вспомнили, что такое деление. Поговорили о составляющих деления. Сказали, какие бывают делители и как результат деления зависит от делителя.

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

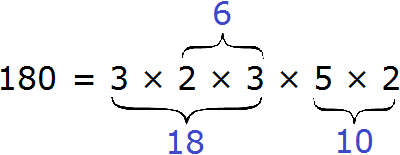
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

Например, разложим предыдущее число 180 этим способом.

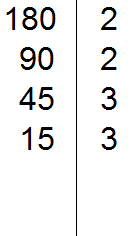
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

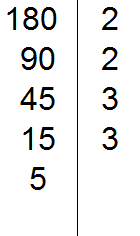
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

5 не делится на 3. Тогда проверяем делится ли 5 на 5.

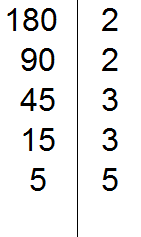
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

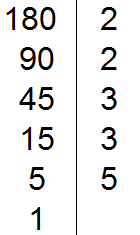
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

Пример 1. Найти делители числа 12

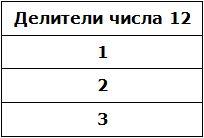
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

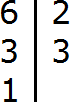
Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник

Закономерности в распределении простых чисел

Введение

Простое число — это натуральное число, имеющее ровно два различных натуральных делителя — единицу и самого себя. Такие числа представляют огромный интерес. Дело в том, что никто так и не смог полностью понять и описать закономерность по которой простые числа располагаются в ряду натуральных чисел.

Ещё до нашей эры Евклид сформулировал и доказал первые теоремы о простых числах. С тех пор математики, среди них Гаусс, Ферма, Риман, Эйлер, продолжали исследования и надо отдать им должное заметно продвинулись. Было обнаружено много интересных свойств простых чисел, выдвинуто много предположений, некоторые из которых были доказаны. Однако много гипотез связанных с простыми числами до сих пор остаются необоснованными.

Распределение простых чисел

Первостепенная задача, решение которой автоматически привело бы к решению большинства вопросов связанных с простыми числами заключается в следующем:

Получить рекуррентную формулу для очередного простого числа

Существует родственная ей задача о количестве простых чисел, не превосходящих заданной величины:

Найти функцию p(x), значение которой в точке x равно числу простых чисел на отрезке [1, x]. Где x – любое действительное число не меньшее единицы.

Функция называется функцией распределения простых чисел.

К решению вышеуказанных задач существует множество подходов. Рассмотрим некоторые из них.

Основная теорема арифметики гласит, что любое натуральное число большее единицы может быть представлено в виде произведения простых множителей (причём единственным образом, с точностью до порядка множителей).

Отсюда и из определения простого числа следует, что натуральное число, большее двух, является простым тогда и только тогда, когда оно не делится ни на одно из простых чисел меньших самого себя.

Первое простое число p₁ =2. Значит все последующие простые числа должны не делится на 2, то есть иметь вид 2k+1, где k – натуральное. То есть все простые числа начиная со второго — нечётные.

Второе простое число p₂ = 3. Значит все последующие простые числа должны иметь вид 3m+1, либо 3m+2, где m – целое. Это равносильно утверждению о том, что все простые числа начиная с третьего не делятся на три. Однако при этом числа ещё должны не делится на два, то есть иметь вид 2k+1.

Решая диофантовы уравнения

найдём k и m и получим, что все простые числа начиная с p₃ обязательно представимы в виде , либо в виде , где t – целое.

И правда, какое бы простое число мы ни взяли оно представимо таким образом:

Однако обратное неверно, то есть любое натуральное число вида 6t+1 или 6t+5 не обязательно простое. Например, .

Третье простое число p₃ = 5. И если по аналогии учесть, что любое простое число, начиная с четвёртого не делится на 5, также не делится на p₁ = 2 и на p₂ = 3, то получим, что все простые числа начиная с p₄ обязательно имеют одно из представлений

Затем учтём p₄, p₅ и т.д. Проблема в том, что на каждом шаге нам придётся решать всё большую систему диофантовых уравнений, поэтому такой прямолинейный подход оказывается весьма сложным.

На самом деле, при различных попытках решения поставленной нами задачи в большом количестве случаев появляются одни и те же конструкции. Например, произведение Эйлера. Рассмотрим, как это происходит, на следующем примере.

Итак, как же найти функцию F(x)? Сначала рассмотрим множество всех натуральных чисел. Какова доля чисел, которые не делятся ни на одно из простых p₁, p₂, …, p_n?

Каждое второе число делится на p₁ = 2. Значит, часть всех чисел делится на p₁.

Каждое третье число делится на 3. Значит, всех чисел делится на p₂. При этом надо учесть, что каждое шестое число делится и на 2 и на 3 одновременно.

Значит, доля чисел не делящихся ни на 2, ни на 3 равна

Если преобразовать выражение, то оно примет вид:

Опять же можно представить выражение в виде

Будем обозначать такое произведение P(n). Кстати, если учесть все простые числа (n→∞), то мы получим обратную величину от так называемого произведения Эйлера.

Почему так происходит? Когда мы получали формулу (1), мы пользовались рассуждениями, что среди всех натуральных чисел доля, делящихся на p_n, равна . Но нельзя сделать такое утверждение о конечном наборе последовательных натуральных чисел. Например, возьмём набор 1,2, 3,4,5,6,7,8,9. Здесь 4 числа из 9 делятся на два. И несложно заметить, что отличается от . То есть, при применении к конечному набору чисел, данный метод даёт результат с некоторой погрешностью.

Это будет мешать далее получать точные формулы. Но если оценить эту погрешность, то можно (например, приняв и используя приведённые выше рассуждения) получить оценку для p_n+1-го простого числа. Однако, получение таких оценок — это тема отдельной работы. И поэтому здесь я не буду на этом останавливаться, а приведу лишь некоторые результаты, полученные математиками.

Одна из оценок для простого числа с номером n:

оценка верна для всех n, начиная с 6.

А вот формула для функции распределения простых чисел:

Для функции Риман получил приближение, используя интегральный логарифм и нетривиальные нули дзета-функции Римана. Однако, это приближение верно, только если верна гипотеза Римана. Причём если гипотеза Римана верна, то оно является наилучшим.

Гипотеза Римана до сих пор не доказана и не опровергнута. Она, как мы могли видеть, тесно связана с простыми числами и, вообще, имеет огромное значение для теории чисел. Из-за своей важной роли в математике, гипотеза Римана была объявлена одной из семи задач тысячелетия.

Проблемы Ландау

Насчёт простых чисел выдвинуто очень много интересных гипотез. Среди них видное место занимают гипотезы Ландау (проблемы Ландау). Формулируются они так:

1. Гипотеза Гольдбаха

Можно ли любое целое чётное число, большее 2, записать в виде суммы двух простых?

2. Гипотеза о числах-близнецах

Бесконечно ли число простых p таких, что p + 2 тоже простое?

3. Гипотеза Лежандра

Всегда ли существует по меньшей мере одно простое число, лежащее между двумя последовательными полными квадратами?

4. Гипотеза о почти квадратных простых числах

Существует ли бесконечно много простых чисел p вида .

Проблемы Ландау ни доказаны, ни опровергнуты по состоянию на 2020 год. Далее кратко расскажу про каждую из них.

1. Гипотеза Гольдбаха

Существуют две гипотезы Гольдбаха: слабая (тернарная) и сильная (бинарная).

Слабая гипотеза Гольдбаха: Каждое нечётное число, большее 5, можно представить в виде суммы трёх простых чисел.

Эту гипотезу доказал Харольд Гельфготт в 2013 году используя так называемые большие дуги. Финальная часть доказательства заняла 133 страницы.

Сильная гипотеза Гольдбаха: Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел.

Надо заметить, что в обоих случаях гипотезы Гольдбаха простые числа не обязательно должны быть различными.

Заметьте, что в сильной гипотезе речь идёт только о чётных числах. Давайте покажем, что нечётное число не обязано быть представимо в виде суммы двух простых чисел. Просто приведём пример. Число 11 не представимо в виде суммы двух простых. Вроде бы несложно.

Но переформулируем проблему так: существует ли такое число, что любое нечётное, большее этого числа, представимо в виде суммы двух простых чисел? Давайте проверим. Пусть существует некоторое нечётное натуральное число N, такое, что любое нечётное число представимо в виде суммы двух простых чисел.

Возьмём произвольное нечётное . По предположению существуют такие простые p₁ и p₂, что . Если сумма двух натуральных чисел нечётна, то это значит, что одно из слагаемых чётно, а другое нет. Пусть для определённости p₁ – чётное. Единственное чётное простое число — это 2. Значит, . То есть, K-2 (предыдущее перед K нечётное число) является простым. Поскольку всё вышесказанное верно для любого нечётного большего N, то получается, что все нечётные числа, начиная с N-2, являются простыми. Это неверно. Если бы это было так, то при n→ ∞. Однако, как говорилось выше при n→ ∞.

Итак, не существует такого числа, начиная с которого все нечётные числа могут быть представлены в виде суммы двух простых.

А что же насчёт чётных? Гипотеза не была опровергнута, не было найдено ни одного контрпримера. Но это не значит, что их не существует. Доказать же гипотезу полностью пока никому не удалось.

2. Гипотеза о числах-близнецах

Бесконечно ли число простых чисел близнецов?

Для начала сформулируем определение. Два простых числа называются близнецами если отличаются друг от друга на 2.

Так же доказано, что существует бесконечно много простых чисел, разница между которыми составляет 246. Это наилучшая из обоснованных на данный момент оценок. Если же использовать некоторые недоказанные гипотезы о простых числах, то оценку можно улучшить.

3. Гипотеза Лежандра

Всегда ли существует, по меньшей мере, одно простое число, лежащее между двумя последовательными полными квадратами?

Аналогичная гипотеза доказана для кубов, начиная с некоторого n. То есть, существует, по меньшей мере, одно простое число, лежащее между и для достаточно большого n. Для квадратов же, гипотеза Лежандра пока не доказана.

4. Почти квадратные простые числа

Заключение

Как мы видим, в этой области теории чисел существует очень много пробелов, а также недоказанных гипотез. Отдельно хочется сказать про численную проверку утверждений. Например, ни для одной из гипотез Ландау не был найден контрпример, даже с использованием значительных вычислительных мощностей в течение большого времени. Однако, в истории математики 20-го и 21-го века были случаи, когда контрпример, опровергающий гипотезу, был настолько огромным числом, что его не удавалось найти с помощью вычислительных машин.

Также, постоянный интерес к простым числам обусловлен их обширным применением в криптографии. Итак, как мы убедились, исследование простых чисел — это, действительно, важная и очень интересная задача.

Источник