Что значит повернутый вокруг оси
Кватернионы для чайников
В данной статье на конкретном примере рассматриваются особенности применения различных методов поворота 3D объекта в пространстве. В частности, сравнивается применение углов Эйлера и кватернионов.
Данная статья пригодится вам, если вы уже прочитали определение кватерниона и давно ищете наглядный материал для того, чтобы понять, зачем придумали кватернионы, и чем же они отличаются от углов Эйлера.
Наглядная демонстрация поворота по углам Эйлера уже была описана в статье на Хабре, особенно интересно поиграть с моделью самолётика (ссылки на программу в той же статье внизу).
Заручившись помощью чудесного сайта tinkercad.com представляю вам более наглядную демонстрацию поворотов предмета по углам Эйлера и сравнение с поворотом на основе кватерниона.
Демонстрация поворотов по углам Эйлера
Поворачивать будем избушку на курьих ножках. Вот ссылка на модель: Izba3D.
Рис. 1. Избушка в изометрии
Поворот вокруг оси Z, а потом оси Y
Рис. 2. Результат поворота рисунка 1 на 90 градусов вокруг оси Z
Рис. 3. Результат поворота рисунка 2 на 90 градусов вокруг оси Y
Поворот вокруг оси Y, а потом оси Z
Рис. 4. Результат поворота рисунка 1 на 90 градусов вокруг оси Y
Рис. 5. Результат поворота рисунка 4 на 90 градусов вокруг оси Z
Сравнение и выводы
Сравним получившиеся картинки:
Рис. 6. Сравнение результатов поворота
Вывод: Порядок применения поворотов влияет на результат.
Кватернион
Гораздо удобнее пользоваться кватернионом, а именно, вектором и величиной поворота вокруг этого вектора.
Допустим, мы хотим повернуть избушку вокруг зелёного крылечка на 90, а потом снова на 90 градусов. Тогда пусть направление вектора совпадает с направлением зелёного крылечка.
Рис. 7. Избушка на курьих ножках с зелёным крылечком
Рис. 8. Поворот на 90 градусов вокруг вектора, совпадающего с крылечком
Рис. 9. Второй поворот на 90 градусов вокруг вектора, совпадающего с крылечком
Значение слова «повёрнутый»
ПОВЁРНУТЫЙ, ая, ое; нут, а, о. Прич. страд. прош. вр. от повернуть.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
повёрнутый
1. страд. прич. прош. вр. от повернуть; подвергшийся поворачиванию вокруг своей оси ◆ Громадный оплот добродетели, который рушится от повёрнутого в дверях ключа и двух рублей лакею на чай!! Аверченко, «Петухов», 1910 г. (цитата из НКРЯ)
2. разг. перен. потерявший чувство меры, повернувшийся на чём-то
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: маркировать — это что-то нейтральное, положительное или отрицательное?
Синонимы к слову «повёрнутый»
Предложения со словом «повёрнутый»
Цитаты из русской классики со словом «повёрнутый»
Понятия со словом «повёрнутый»
Отправить комментарий
Дополнительно
Предложения со словом «повёрнутый»
Если положить месячного младенца на спинку с повёрнутой головой, рука с этой стороны вытянется, а противоположная согнётся в локте.
Даже тренер улыбнулся, а водитель, вывернув шею, так и ехал с рыдающим от смеха и повёрнутым назад лицом.
Вскоре уже всё в аудитории следят за действиями маленького мальчика в бейсбольной кепке, повёрнутой козырьком назад.
Синонимы к слову «повёрнутый»
Морфология
Правописание
Карта слов и выражений русского языка
Онлайн-тезаурус с возможностью поиска ассоциаций, синонимов, контекстных связей и примеров предложений к словам и выражениям русского языка.
Справочная информация по склонению имён существительных и прилагательных, спряжению глаголов, а также морфемному строению слов.
Сайт оснащён мощной системой поиска с поддержкой русской морфологии.
Вращение и кватернионы. Сборник рецептов.
Давайте коротко определимся с терминологией. Каждый представляет себе, что такое ориентация объекта. Термин «ориентация» подразумевает, что мы находимся в некоторой заданной системе отсчета. Например, фраза «он повернул голову влево» осмыслена только тогда, когда мы представляем, где находится «лево» и где находилась до этого голова. Это важный для понимания момент, ведь если бы это был монстр с головой на животе макушкой вниз то фраза «он повернул голову влево» уже не покажется такой однозначной.
При слове ориентация часто возникают ассоциация с направлением. Часто можно услышать фразы подобные «он повернул голову в сторону приближающегося локомотива». Например, ориентацию автомобиля можно было бы описать направлением, в котором смотрят его фары. Однако направление задается двумя параметрами (например, как в сферической системе координат), а объекты в трехмерном пространстве имеют три степени свободы (вращения). В случае с автомобилем он может смотреть в одном направлении как стоя на колесах, так и лежа на боку или на крыше. Ориентацию действительно можно задать направлением, но их потребуется два. Давайте рассмотрим ориентацию на простом примере головы человека.
Договоримся про исходное положение, в котором голова ориентирована по умолчанию (без вращения). За исходное примем положение, в котором голова смотрит лицом по направлению оси «z», а вверх (макушкой) смотрит по направлению оси «y». Назовем направление, в котором повернуто лицо «dir» (без вращения совпадает с «z»), а направление, куда смотрит макушка «up» (без вращения совпадает с «y»). Теперь у нас есть точка отсчета, есть локальная координатная система головы «dir», «up» и глобальная с осями x, y, z. Произвольно повернем голову и отметим, куда смотрит лицо. Глядя в этом же направлении можно вращать голову вокруг оси, совпадающей с направлением взгляда «dir». Например, наклонив голову на бок (прижавшись щекой к плечу) мы будем смотреть в том же направлении, но ориентация головы поменяется. Чтобы зафиксировать поворот вокруг направления взгляда, используем еще и направление «up» (направленно к макушке). В этом случае мы однозначно описали ориентацию головы и не сможем ее повернуть, не изменив направления осей «dir» и «up».
Мы рассмотрели достаточно естественный и простой способ задания ориентации с помощью двух направлений. Как же описать наши направления в программе, чтобы ими было удобно пользоваться? Простой и привычный способ хранить эти направления в виде векторов. Опишем направления с помощью векторов длиной в единицу (единичных векторов) в нашей глобальной системе координат xyz. Первый важный вопрос, как бы наши направления передать в понятном виде графическому API? Графические API работают в основном с матрицами. Нам бы хотелось получить матрицу поворота из имеющихся векторов. Два вектора описывающие направление «dir» и «up» и есть та самая матрица поворота, а точнее два компонента матрицы поворота 3×3. Третий компонент матрицы мы можем получить из векторного произведения векторов «dir» и «up» (назовем его «side»). В примере с головой вектор «side» будет смотреть в направлении одного из ушей. Матрица поворота это и есть координаты трех векторов «dir», «up» и «side» после поворота. Эти вектора до поворота совпадали с осями глобальной системы координат xyz. Именно в виде матрицы поворота очень часто и хранят ориентацию объектов (иногда матрицу хранят в виде трех векторов). Матрицей можно задать ориентацию (если известна ориентация по умолчанию) и поворот.
Похожий способ представления ориентации, называется углы Эйлера (Euler Angles), с тем лишь отличием, что направление «dir» задается в сферических координатах, а «up» описывается одним углом поворота вокруг «dir». В итоге получим три угла вращения вокруг взаимно перпендикулярных осей. В аэродинамике их называют Крен, Тангаж, Рысканье (Roll, Pitch, Yaw или Bank, Heading, Attitude). Крен (Roll) — это наклон головы вправо или влево (к плечам), поворот вокруг оси проходящей через нос и затылок. Тангаж (Pitch) — это наклон головы вверх и вниз, вокруг оси проходящей через уши. И Рысканье (Yaw) — это повороты головы вокруг шеи. Надо помнить, что повороты в трехмерном пространстве не коммутативны, а значит, на результат влияет порядок поворотов. Если мы повернем на R1 а потом на R2, ориентация объекта не обязательно совпадет с ориентацией при повороте на R2 и затем на R1. Именно поэтому при использовании Углов Эйлера важен порядок поворотов вокруг осей. Обратите внимание, что математика углов Эйлера зависит от выбранных осей (мы использовали только один из возможных вариантов), от порядка поворота вокруг них, а также от того в какой системе координат совершаются повороты, в мировой или локальной объекта. В углах Эйлера можно хранить и вращение и поворот.
Огромный недостаток такого представления, отсутствие операции комбинации поворота. Не пытайтесь складывать покомпонентно углы Эйлера. Итоговый поворот не будет комбинацией исходных поворотов. Это одна из самых распространенных ошибок начинающих разработчиков. Чтобы повернуть объект, храня вращение в углах Эйлера, нам придется перевести вращение в другую форму, например в матрицу. Затем перемножить матрицы двух поворотов и из итоговой матрицы извлечь углы Эйлера. Проблема усложняется еще и тем что в частных случаях прямое сложение углов Эйлера работает. В случае комбинации вращений вокруг одной и той же оси, этот метод математически верен. Повернув на 30 градусов вокруг оси X, а затем еще раз вокруг X на 40 градусов мы получим поворот вокруг X на 70 градусов. В случае вращений по двум осям простое сложение углов может давать некий «ожидаемый» результат. Но как только появляется поворот по третьей оси, ориентация начинает вести себя непредсказуемо. Многие разработчики тратят месяцы труда чтобы заставить работать камеру «правильно». Рекомендую обратить пристальное внимание к этому недостатку, особенно если вы уже решили использовать углы Эйлера для представления вращений. Начинающим программистам кажется что, использовать углы Эйлера проще всего. Позволю себе высказать личное мнение, что математика углов Эйлера намного сложнее и коварнее чем математика кватернионов.
Углы Эйлера это комбинация (композиция) вращений вокруг базовых осей. Существует еще один, простой, способ задания вращения. Этот способ можно назвать «смесь» вращений вокруг базовых координатных осей, или просто вращение вокруг произвольной фиксированной оси. Три компоненты описывающие вращение образуют вектор, лежащий на оси, вокруг которой и поворачивается объект. Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах (Axis Angle). Выбрав подходящую ось и угол можно задать любую ориентацию объекта. В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора в этом случае совпадает с направлением оси вращения, а длина его равна углу поворота. В физике, таким образом, хранят угловую скорость. Вектор, совпадающий направлением с осью вращения и длиной представляющей скорость в радианах в секунду.
Кватернион
После краткого обзора о представлениях ориентации можно перейти к знакомству с кватернионом.
Кватернион — это четверка чисел, которые ввел в обращение (как считают историки) Уильям Гамильтон в виде гиперкомплексного числа. В этой статье я предлагаю рассматривать кватернион как четыре действительных числа, например как 4d вектор или 3d вектор и скаляр.
Существуют и другие представления кватерниона, которые я не буду рассматривать.
Как же хранят вращение в кватернионе? Практически также как и в «Axis Angle» представлении, первые три компонента представляют вектор, лежащий на оси вращения, причем длина вектора зависит от угла поворота. Четвертый компонент зависит только от величины угла поворота. Зависимость довольно простая — если взять единичный вектор V за ось вращения и угол alpha за вращение вокруг этой оси, тогда кватернион представляющий это вращение
можно записать как:
Для понимания того, как хранит вращение кватернион, вспомним про двумерные вращения. Вращение в плоскости можно задать матрицей 2×2, в которой будут записаны косинусы и синусы угла поворота. Можно представить, что кватернион хранит комбинацию оси вращения и матрицы половины поворота вокруг этой оси.
Метод вращения вокруг оси
Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.
Способ вращения вокруг проецирующей прямой
Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.
Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.
При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’1 так, чтобы выполнялось условие C’1D’1 || X. Для нахождения точки C»1 из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’1.
На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.
Сначала вращением вокруг оси i1 CD перемещают в положение C1D1, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i2 отрезок переводится в искомое положение C2D2, где он перпендикулярен горизонтальной плоскости проекции.
Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i1 проходит через точку D, а проекция i»2 фронтально проецирующей прямой i2 лежит на продолжении отрезка C»1D»1.
Способ вращения вокруг линии уровня
Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.
Основные правила построения
Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.
Поворот вокруг оси
Поворот вокруг оси
В двумерном пространстве команда ROTATE производит поворот объекта вокруг указанной точки; при этом направление поворота определяется текущей ПСК. При работе в трехмерном пространстве объект поворачивается вокруг оси. Ось может определяться указанием двух точек, объекта, одной из осей координат (Х, Y или Z) или текущего направления взгляда. Для поворота трехмерных объектов можно использовать как команду ROTATE, так и ее трехмерный аналог.
Запросы команды 3DROTATE:
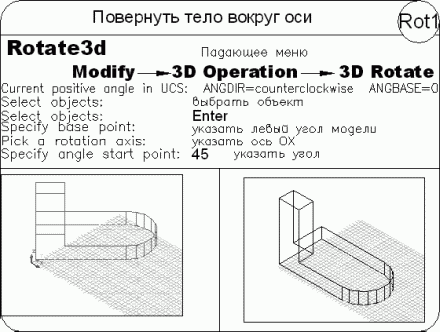
Current positive angle in UCS: ANGDIR=counterclockwise ANGBASE=0 – текущие установки отсчета углов в ПСК
Select objects: – выбрать объекты для поворота
Select objects: – нажать клавишу Enter для окончания выбора объектов
Specify base point: – указать базовую точку
Pick a rotation axis: – указать ось вращения
Specify angle start point: – указать точку на первом луче угла
Specify angle end point: – указать точку на втором луче угла
Команда ROTATE3D осуществляет поворот объектов в трехмерном пространстве вокруг заданной оси.
Запросы команды ROTATE3D:
Current positive angle: ANGDIR=counterclockwise ANGBASE=0 – текущие установки отсчета углов
Select objects: – выбрать объекты
Select objects: – нажать клавишу Enter для окончания выбора объектов
Specify first point on axis or defi ne axis by [Object/Last/View/Xaxis/Yaxis/Zaxis/2points]: – указать первую точку оси
Specify second point on axis: – указать вторую точку оси
Specify rotation angle or [Reference]: – указать угол поворота
Ключи команды ROTATE3D:
• Object – поворот вокруг выбранного объекта. Такими объектами могут быть отрезок, окружность, дуга или сегмент двумерной полилинии;
• Last – поворот вокруг оси, использовавшейся в предыдущей команде поворота;
• View – поворот вокруг оси, выровненной вдоль направления вида текущего видового экрана и проходящей через заданную точку;
• Xaxis, Yaxis, Zaxis – поворот вокруг оси, выровненной соответственно вдоль направления оси X, Y или Z и проходящей через заданную точку;
• 2point – поворот вокруг оси, проходящей через две заданные точки.
Тренинг-система
Выполните упражнение Rot1 из раздела 5.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Рамка вокруг изображения
Рамка вокруг изображения Кроме регулировки расстояния до текста, есть еще один способ отделить картинку от остального содержимого страницы.Отделить изображение от текста можно, поступив с ним, как с обычной картиной: поставив в рамку. Это делается с помощью атрибута border,
Вокруг модулей
Вокруг модулей В этой главе были рассмотрены особенности написания, сборки, загрузки и выгрузки модулей ядра. Мы обсудили, что такое модули и каким образом ядро операционной системы Linux, несмотря на то что оно является монолитным, может загружать код динамически. Были
6.3.2.1. Поворот
6.3.2.1. Поворот Предположим, что вы сделали вертикальную фотографию, но при просмотре она будет отображаться как горизонтальная. Для удобного просмотра на экране компьютера фотографию нужно повернуть.Запустите GIMP и откройте (комбинация клавиш ‹Ctrl+O›) нужную фотографию
Глава 11 Вокруг Интернета
Глава 11 Вокруг Интернета Яндекс — это не только поиск, и не только сервисы, предоставляемые компанией. Это еще и множество иных проектов, в той или иной степени связанных с
Lathe (Вращение вокруг оси)
Lathe (Вращение вокруг оси) Модификатор Lathe (Вращение вокруг оси) является одним из наиболее применяемых. Он используется для создания тел методом поворота вокруг своей оси половины профиля сечения объекта. Примерами объектов такого рода могут служить большая часть
10.4.6. Обертка вокруг DBI
10.4.6. Обертка вокруг DBI Теоретически интерфейс DBI обеспечивает доступ к любым базам данных. Иными словами, один и тот же код должен работать и с Oracle, и с MySQL, и с PostgreSQL, и с любой другой СУБД, стоит лишь изменить одну строку, в которой указан нужный адаптер. Иногда эта идеология
Поворот вокруг оси
Поворот вокруг оси В двумерном пространстве команда ROTATE производит поворот объекта вокруг указанной точки; при этом направление поворота определяется текущей ПСК. При работе в трехмерном пространстве объект поворачивается вокруг оси. Ось может определяться указанием
Поворот вокруг оси
Поворот вокруг оси В двумерном пространстве команда ROTATE производит поворот объекта вокруг указанной точки; при этом направление поворота определяется текущей ПСК. При работе в трехмерном пространстве объект поворачивается вокруг оси. Ось может определяться указанием
Поворот вокруг оси
openSUSE 12.2: детектив вокруг релиза
openSUSE 12.2: детектив вокруг релиза LinuxFormat, #162 (октябрь 2012)Когда вы будете читать этот номер, выход означенного релиза будет состоявшимся фактом. Однако ему предшествовала почти детективная история. 31 августа «по России слух прошёл», что на официальных зеркалах проекта лежат
Глава 5 Компьютеры вокруг. Все для человека
Глава 5 Компьютеры вокруг. Все для человека Всегда и везде человек хотел жить долго и без болезней, в достатке и без тяжелой физической работы. И, конечно, в безопасности. Сегодня реализации этих базисных целей служат многие другие виды человеческой деятельности. Именно
Возня вокруг выключателя питания
Возня вокруг выключателя питания Энтузиасты видеонаблюдения, такие как Брин и Манн, считали, что со временем видеокамер будет все больше и больше. А в мире, заполненном видеокамерами, утверждали они, у нас всего два варианта: либо камеры целиком и полностью находятся под