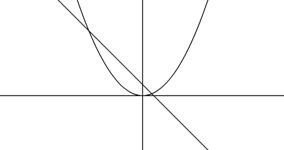
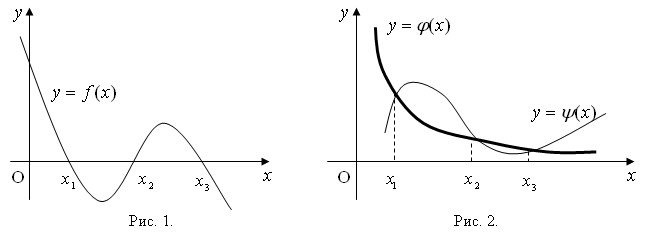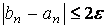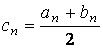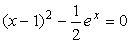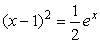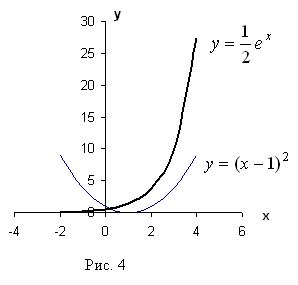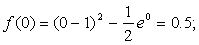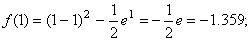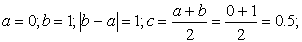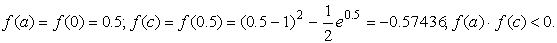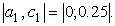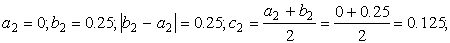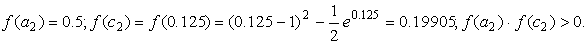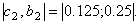Что значит отделить корни уравнения
Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
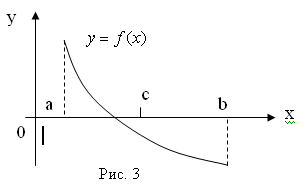
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
Что значит отделить корни уравнения
1. Приближенное решение нелинейных уравнений
Пусть дано уравнение с одним неизвестным
Будем предполагать, что уравнение (1.1) имеет лишь изолированные корни, то есть для каждого корня существует окрестность, не содержащая других корней этого уравнения.
Приближенное решение уравнения состоит из двух этапов:
1. Отделение корней, то есть нахождение интервалов из области определения функции f ( x ), в каждом из которых содержится только один корень уравнения (1).
2. Уточнение корней до заданной точности.
Отделение корней можно проводить графически и аналитически.
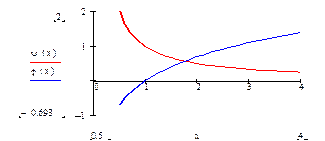
с точностью ε = 0,0001. Отделим корень графически. Для этого преобразуем уравнение к виду
и построим графики функций (рис. 4):
Из рисунка видно, что абсцисса точки пересечения этих графиков принадлежит отрезку [0; 1].
Подтвердим аналитически правильность нахождения отрезка изоляции корня. Для отрезка [0; 1] имеем:
Уточнение корня выполним методом половинного деления.
Корень принадлежит отрезку
Корень принадлежит отрезку
Корень принадлежит отрезку
Вычислительная математика копия 1
Уравнение называется алгебраическим, если его можно представить в виде:
Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.
Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.
1.1 Отделение корня
Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.
Корень можно отделить аналитически и графически.
Графический метод отделения корня
1.2 Уточнение корня методом деления отрезка пополам
Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.
1.3 Метод хорд
TL; DR (слишком долго; не читал)
Чтобы решить уравнение с квадратным корнем, сначала выделите квадратный корень с одной стороны уравнения. Затем возведите в квадрат обе стороны уравнения и продолжайте решение для переменной. Не забудьте проверить свою работу в конце.
Простой пример
Изолировать квадратный корень
Используйте арифметические операции, такие как сложение, вычитание, умножение и деление, чтобы выделить выражение квадратного корня на одной стороне уравнения. Например, если исходное уравнение было √ x + 1 = 5, вы бы вычли 1 из обеих частей уравнения, чтобы получить следующее:
Квадрат обе стороны уравнения
Возведение в квадрат обеих сторон уравнения устраняет знак квадратного корня. Это дает вам:
Или, как только упростили:
Вы удалили знак квадратного корня, и у вас есть значение для x, поэтому ваша работа здесь завершена. Но подождите, есть еще один шаг:
Проверь свою работу
Проверьте свою работу, подставив найденное вами значение x в исходное уравнение:
Немного более сложный пример
Что если у вас есть более сложное выражение под знаком радикала (квадратный корень)? Рассмотрим следующее уравнение. Вы все еще можете применить тот же процесс, который использовался в предыдущем примере, но это уравнение выдвигает на первый план пару правил, которым вы должны следовать.
Изолировать радикальное
Как и раньше, используйте операции, такие как сложение, вычитание, умножение и деление, чтобы выделить выражение радикала на одной стороне уравнения. В этом случае вычитание 5 с обеих сторон дает вам:
Предупреждения
Обратите внимание, что вас просят изолировать квадратный корень (который предположительно содержит переменную, потому что, если бы она была константой вроде √9, вы могли бы просто решить ее на месте; √9 = 3). Вас не просят изолировать переменную. Этот шаг наступает позже, после того как вы удалили знак квадратного корня.
Квадрат обе стороны
Возведите в квадрат обе стороны уравнения, что дает вам следующее:
Предупреждения
Обратите внимание, что вы должны поставить квадрат под знаком радикала, а не только в переменной.
Изолировать переменную
Теперь, когда вы удалили корень или квадратный корень из уравнения, вы можете изолировать переменную. Чтобы продолжить пример, добавив 4 к обеим сторонам уравнения, вы получите:
Проверь свою работу
Как и прежде, проверьте свою работу, подставив найденное вами значение y обратно в исходное уравнение. Это дает вам:
Упрощение радикала дает вам:
29 = 29, верное утверждение, которое указывает на действительный результат.
Как оценить логарифмы с основанием квадратного корня
Как оценить, используя кривую квадратного корня
Как получить ответ квадратного корня из квадратного корня на Ти-84
Чтобы найти квадратный корень с помощью моделей Texas Instruments TI-84, найдите символ квадратного корня. Эта вторая функция находится над клавишей x в квадрате на всех моделях. Нажмите вторую функциональную клавишу в левом верхнем углу клавиатуры и выберите клавишу х в квадрате. Введите значение, о котором идет речь, и нажмите Enter.
3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней 

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то


Тогда все положительные корни многочлена лежат в интервале


Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.






Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0


 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4



 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
 Министерство образования и науки РФ
Министерство образования и науки РФ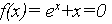 видим, что
видим, что 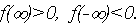 Обнаружив, что
Обнаружив, что 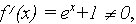 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).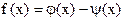 и строить графики функций
и строить графики функций 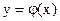 и
и 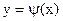 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.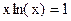 .
.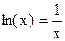 , т.е.
, т.е. 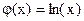 и
и 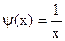 .
.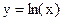 и
и 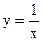 .
.