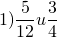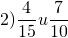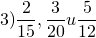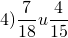Что значит общий знаменатель
Общий знаменатель, понятие и определение.
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь \(\frac<1><20>\) домножить на 7, чтобы получить знаменатель 140.
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей \(\frac<2><11>, \frac<1><15>, \frac<3><22>\)
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби \(\frac<2><11>, \frac<1><15>, \frac<3><22>\) к общему знаменатели равному 330.
Вопросы по теме:
Какой общий знаменатель у дробей \(\bf \frac<2><25>\) и \(\bf \frac<1><14>\)?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей \(\frac<2><25>\) и \(\frac<1><14>\) знаменателем может быть число 700, 1400 и т.д.
Приведение дроби к наименьшему общему знаменателю: правило, примеры решений
В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Приведение дробей к общему знаменателю
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Пример 1. Общий знаменатель
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
По правилу, сначала найдем НОК знаменателей дробей.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
Далее вычислим дополнительные множители для каждой дроби.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
3 2 · 36 = 108 72 5 6 · 12 = 60 72 3 8 · 9 = 27 72 17 18 · 4 = 68 72
Наименьший общий знаменатель (НОЗ) алгебраических дробей, его нахождение
Большинство действий с алгебраическими дробями, такие, например, как сложение и вычитание, требуют предварительного приведения этих дробей к одинаковым знаменателям. Такие знаменатели также часто обозначаются словосочетанием «общий знаменатель». В данной теме мы рассмотрим определение понятий «общий знаменатель алгебраических дробей» и «наименьший общий знаменатель алгебраических дробей (НОЗ)», рассмотрим по пунктам алгоритм нахождения общего знаменателя и решим несколько задач по теме.
Общий знаменатель алгебраических дробей
Общий знаменатель алгебраических дробей определяется похожим образом, только вместо чисел используются многочлены, так как именно они стоят в числителях и знаменателях алгебраической дроби.
Общий знаменатель алгебраической дроби – это многочлен, который делится на знаменатель любой из дробей.
В связи с особенностями алгебраических дробей, речь о которых пойдет ниже, мы чаще будем иметь дело с общими знаменателями, представленными в виде произведения, а не в виде стандартного многочлена.
Наименьший общий знаменатель (НОЗ)
Для заданных алгебраических дробей количество общих знаменателей может быть бесконечное множество.
При решении задач можно облегчить себе работу, используя общий знаменатель, который среди всего множества знаменателей имеет самый простой вид. Такой знаменатель часто обозначается как наименьший общий знаменатель.
Наименьший общий знаменатель алгебраических дробей – это общий знаменатель алгебраических дробей, который имеет самый простой вид.
К слову, термин «наименьший общий знаменатель» не является общепризнанным, потому лучше ограничиваться термином «общий знаменатель». И вот почему.
Ранее мы сфокусировали ваше внимание на фразе «знаменатель самого простого вида». Основной смысл этой фразы следующий: на знаменатель самого простого вида должен без остатка делиться любой другой общий знаменатель данных в условии задачи алгебраических дробей. При этом в произведении, которое является общим знаменателем дробей, можно использовать различные числовые коэффициенты.
Нахождение общего знаменателя алгебраических дробей: алгоритм действий
Предположим, что у нас имеется несколько алгебраических дробей, для которых нам необходимо отыскать общий знаменатель. Для решения этой задачи мы можем использовать следующий алгоритм действий. Сначала нам необходимо разложить на множители знаменатели исходных дробей. Затем мы составляем произведение, в которое последовательно включаем:
Полученное произведение и будет общим знаменателем алгебраических дробей.
В качестве множителей произведения мы можем взять все знаменатели дробей, данных в условии задачи. Однако множитель, который мы получим в итоге, по смыслу будет далек от НОЗ и использование его будет иррациональным.
Решение
В данном случае у нас нет необходимости раскладывать знаменатели исходных дробей на множители. Потому начнем применять алгоритм с составления произведения.
Теперь рассмотрим примеры задач, когда в знаменателях алгебраических дробей есть целые числовые множители. В таких случаях мы также действуем по алгоритму, предварительно разложив целые числовые множители на простые множители.
Решение
Если внимательно посмотреть на результаты двух разобранных примеров, то можно заметить, что общие знаменатели дробей содержат все множители, присутствующие в разложениях знаменателей, причем если некоторый множитель имеется в нескольких знаменателях, то он берется с наибольшим из имеющихся показателей степени. А если в знаменателях имеются целые коэффициенты, то в общем знаменателе присутствует числовой множитель, равный наименьшему общему кратному этих числовых коэффициентов.
Теперь мы можем записать еще один алгоритм нахождения общего множителя алгебраических дробей. Для этого мы:
Приведенные алгоритмы равноценны, так что использовать в решении задач можно любой из них. Важно уделять внимание деталям.
Встречаются случаи, когда общие множители в знаменателях дробей могут быть незаметны за числовыми коэффициентами. Здесь целесообразно сначала вынести числовые коэффициенты при старших степенях переменных за скобки в каждом из множителей, имеющихся в знаменателе.
Решение
Данные в условии задачи дроби могут иметь дробные коэффициенты. В этих случаях необходимо сначала избавиться от дробных коэффициентов путем умножения числителя и знаменателя на некоторое число.
Решение
Общий знаменатель дробей
Это правило позволяет легко и быстро устно найти наименьший общий знаменатель дробей.
Правило нахождения наименьшего общего знаменателя для двух или нескольких дробей:
1) Выбираем из всех знаменателей наибольшее число и проверяем, делится ли оно на остальные. Если делится, то это число и есть наименьший общий знаменатель (НОЗ) этих дробей.
2) Если наибольший знаменатель не делится на все остальные, умножаем его на 2 и проверяем, делится ли полученное число на все остальные. Если делится, то это новое число и есть НОЗ.
3) Если после умножения на два новое число не делится на все остальные, наибольший из знаменателей умножаем на 3,4,5 и так далее до тех пор, пока новое число не будет делиться на все остальные. Это новое число и есть наименьший общий знаменатель.
Найти общий знаменатель дробей:
Выбираем бОльший знаменатель и проверяем, делится ли он на меньший. 12 на 4 делится. Значит, наименьший общий знаменатель этих дробей равен 12.
Выбираем больший знаменатель и проверяем, делится ли он на меньший. 15 на 10 не делится. Умножаем бОльший знаменатель на 2 и проверяем, делится ли новое число на меньший знаменатель. 15∙2=30, 30 на 10 делится. Значит, наименьший общий знаменатель этих дробей равен 30.
Выбираем большее число и проверяем, делится ли оно на остальные. 20 на 15 и 12 не делится. Большее число умножаем на 2 и проверяем, делится ли новое число на остальные. 20∙2=40. 40 на 15 и 12 не делится. Значит, большее число 20 надо умножить на 3 и проверить, будет ли делиться результат на остальные. 20∙3=60. 60 делится и на 15, и на 12. Поэтому 60 — наименьший общий знаменатель этих дробей.
Большее — 18. Оно не делится на меньшее — 15. Умножаем большее на 2: 18∙2=36. 36 на 15 не делится. Умножаем большее на 3: 18 ∙3=54. 54 на 15 не делится. Умножаем большее на 4: 18∙4=72. 72 на 15 не делится. Умножаем большее на 5: 18∙5=90. 90 на 15 делится. Значит, наименьший общий знаменатель этих дробей равен 90.
В следующий раз мы посмотрим, как это правило применять при сложении и вычитании дробей с разными знаменателями.
Обыкновенные дроби
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо: