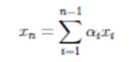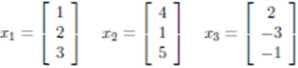Что значит нормализовать матрицу

Лучшие способы нормализации массива Numpy

Привет гики и добро пожаловать в этой статье мы рассмотрим Нормализацию массива NumPy. Вы можете разделить эту статью на 2 раздела, которые были в

Лучшие способы нормализации массива Numpy

Привет гики и добро пожаловать в этой статье мы рассмотрим Normalize NumPy array. Вы можете разделить эту статью на 2 раздела. В 1-м разделе мы рассмотрим массив NumPy. Тогда как во втором мы рассмотрим, как нормализовать его. Чтобы достичь полного понимания этой темы, мы рассмотрим ее синтаксис и параметр. Затем мы увидим применение всей теоретической части на нескольких примерах. Но прежде чем двигаться так далеко вперед, давайте кратко разберемся в этих двух вещах.

Массив NumPy

Как обсуждалось ранее, массив Numpy помогает нам в создании массивов. В этом разделе мы рассмотрим синтаксис и различные параметры, связанные с ним. Наряду с этим мы также рассмотрим некоторые примеры.

Синтаксис массива NumPy

Это общий синтаксис функции. Он имеет несколько параметров, связанных с ним, которые мы рассмотрим в следующем разделе.

Параметры

Этот параметр представляет входной массив, который мы хотим получить в качестве выходного.

метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере. href=”https://en.wikipedia.org/wiki/Method”>метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере.

3. Нормализация с помощью понимания списка

Вы также можете нормализовать список в python. Понимание списка, как правило, предлагает более короткий синтаксис, который помогает в создании нового списка из существующего списка. Давайте рассмотрим это на примере.

Посмотрите, как нам удалось нормализовать наш существующий список. Здесь мы видим, что мы разделили каждый элемент в списке на сумму всех элементов. Это тоже хороший вариант для нормализации.

4. Нормализация с использованием цикла For

Мы также продвигаем процесс нормализации с помощью цикла for. Используя цикл for, мы можем вычислить сумму всех элементов. Затем разделите каждый элемент на эту сумму. Здесь я советую вам использовать массив NumPy. Продолжая деление, вы можете получить ошибку, так как “list/int” не является подходящим типом данных.

Вывод

В этой статье мы рассмотрели нормализованный массив NumPy. Для этого сначала мы рассмотрели массив NumPy вместе с его синтаксисом, параметрами и примером. Затем в следующем разделе мы рассмотрели, как нормализовать массив.

Надеюсь, эта статья смогла развеять все сомнения. Но если у вас есть какие-либо нерешенные вопросы, не стесняйтесь писать их ниже в разделе комментариев. Прочитав это, почему бы не прочитать о Syslog далее.

Источник

2 простых способа нормализовать данные в Python

В этом руководстве мы узнаем, как нормализовать данные в Python. При нормализации меняем масштаб данных. Чаще всего масштабирование данных изменяется в диапазоне от 0 до 1.

Почему нам нужно нормализовать данные в Python?

Алгоритмы машинного обучения, как правило, работают лучше или сходятся быстрее, когда различные функции (переменные) имеют меньший масштаб. Поэтому перед обучением на них моделей машинного обучения данные обычно нормализуются.

Нормализация также делает процесс обучения менее чувствительным к масштабу функций. Это приводит к улучшению коэффициентов после тренировки.

Этот процесс повышения пригодности функций для обучения путем изменения масштаба называется масштабированием функций.

Формула нормализации приведена ниже:

Шаги по нормализации данных в Python

Мы собираемся обсудить два разных способа нормализации данных в Python.

Использование normalize() из sklearn

Начнем с импорта processing из sklearn.

Теперь мы можем использовать метод normalize() для массива. Этот метод нормализует данные по строке. Давайте посмотрим на метод в действии.

Полный код

Вот полный код из этого раздела:

Мы видим, что все значения теперь находятся в диапазоне от 0 до 1. Так работает метод normalize() в sklearn.

Вы также можете нормализовать столбцы в наборе данных, используя этот метод.

Нормализовать столбцы в наборе данных с помощью normalize()

Поскольку normalize() нормализует только значения по строкам, нам нужно преобразовать столбец в массив, прежде чем применять метод.

Чтобы продемонстрировать, мы собираемся использовать набор данных California Housing.

Начнем с импорта набора данных.

Как нормализовать набор данных без преобразования столбцов в массив?

Давайте посмотрим, что произойдет, когда мы попытаемся нормализовать набор данных без преобразования функций в массивы для обработки.

Здесь значения нормализованы по строкам, что может быть очень неинтуитивно. Нормализация по строкам означает, что нормализуется каждая отдельная выборка, а не признаки.

Однако вы можете указать ось при вызове метода для нормализации по элементу (столбцу).

Значение параметра оси по умолчанию установлено на 1. Если мы изменим значение на 0, процесс нормализации произойдет по столбцу.

Вы можете видеть, что столбец total_bedrooms в выходных данных совпадает с столбцом, который мы получили выше после преобразования его в массив и последующей нормализации.

Использование MinMaxScaler() для нормализации данных в Python

Когда дело доходит до нормализации данных, Sklearn предоставляет еще один вариант: MinMaxScaler.

Это более популярный выбор для нормализации наборов данных.

Вот код для нормализации набора данных жилья с помощью MinMaxScaler:

Вы можете видеть, что значения на выходе находятся между (0 и 1).

MinMaxScaler также дает вам возможность выбрать диапазон функций. По умолчанию диапазон установлен на (0,1). Посмотрим, как изменить диапазон на (0,2).

Значения на выходе теперь находятся в диапазоне (0,2).

Вывод

Это два метода нормализации данных в Python. Мы рассмотрели два метода нормализации данных в разделе sklearn. Надеюсь, вам было весело учиться с нами!

Источник

Умная нормализация данных

Эта статья появилась по нескольким причинам.

Во-первых, в подавляющем большинстве книг, интернет-ресурсов и уроков по Data Science нюансы, изъяны разных типов нормализации данных и их причины либо не рассматриваются вообще, либо упоминаются лишь мельком и без раскрытия сути.

Во-вторых, имеет место «слепое» использование, например, стандартизации для наборов с большим количеством признаков — “чтобы для всех одинаково”. Особенно у новичков (сам был таким же). На первый взгляд ничего страшного. Но при детальном рассмотрении может выясниться, что какие-то признаки были неосознанно поставлены в привилегированное положение и стали влиять на результат значительно сильнее, чем должны.

И, в-третьих, мне всегда хотелось получить универсальный метод учитывающий проблемные места.

Повторение — мать учения

Нормализация — это преобразование данных к неким безразмерным единицам. Иногда — в рамках заданного диапазона, например, [0..1] или [-1..1]. Иногда — с какими-то заданным свойством, как, например, стандартным отклонением равным 1.

Ключевая цель нормализации — приведение различных данных в самых разных единицах измерения и диапазонах значений к единому виду, который позволит сравнивать их между собой или использовать для расчёта схожести объектов. На практике это необходимо, например, для кластеризации и в некоторых алгоритмах машинного обучения.

Аналитически любая нормализация сводится к формуле

где — текущее значение,
— величина смещения значений,
— величина интервала, который будет преобразован к “единице”

По сути всё сводится к тому, что исходный набор значений сперва смещается, а потом масштабируется.

Минимакс (MinMax). Цель — преобразовать исходный набор в диапазон [0..1]. Для него:
= , минимальное значение исходных данных.
= — , т.е. за “единичный” интервал берется исходный диапазон значений.

Стандартизация. Цель — преобразовать исходный набор в новый со средним значением равным 0 и стандартным отклонением равным 1.
= , среднее значение исходных данных.
— равен стандартному отклонению исходного набора.

Для других методов всё аналогично, но со своими особенностями.

В большинстве методов кластеризации или, например, классификации методом ближайших соседей необходимо рассчитывать меру “близости” между различными объектами. Чаще всего в этой роли выступают различные вариации евклидового расстояния.

Представим, что у Вас есть какой-то набор данных с несколькими признаками. Признаки отличаются и по типу распределения, и по диапазону. Чтобы можно было с ними работать, сравнивать, их нужно нормализовать. Причём так, чтобы ни у какого из них не было преимуществ перед другими. По крайней мере, по умолчанию — любые такие предпочтения Вы должны задавать сами и осознанно. Не должно быть ситуации, когда алгоритм втайне от Вас сделал, например, цвет глаз менее важным, чем размер ушей*

* нужно сделать небольшое примечание — здесь речь идёт не о важности признака для, например, результата классификации (это определяется на основе самих данных при обучении модели), а о том, чтобы до начала обучения все признаки были равны по своему возможному влиянию.

Итого, главное условие правильной нормализации — все признаки должны быть равны в возможностях своего влияния.

Шаг 1 — определяем смещение

Чаще всего данные центрируют — т.е. определяют, значение, которое станет новым 0 и “сдвигают” данные относительно него.

Что лучше взять за центр? Некоего «типичного представителя» Ваших данных. Так при использовании стандартизации используется среднее арифметическое значение.

Здесь проявляется проблема № 1 — различные типы распределений не позволяют применять к ним методы, созданные для нормального распределения.

Если Вы спросите любого специалиста по статистике, какое значение лучше всего показывает “типичного представителя” совокупности, то он скажет, что это — медиана, а не среднее арифметическое. Последнее хорошо работает только в случае нормального распределения и совпадает с медианой (алгоритм стандартизации вообще оптимален именно для нормального распределения). А у Вас распределения разных признаков могут (и скорее всего будут) кардинально разные.

Вот, например, различия между медианой и средним арифметическим значением для экспоненциального распределения.

А вот так выглядят эти различия при добавлении выброса:

В отличии от среднего значения медиана практически не чувствительна к выбросам и асимметрии распределения. Поэтому её оптимально использовать как “нулевое” значение при центрировании.

В случае, когда нужно не центрировать, а вписать в заданный диапазон, смещением является минимальное значение данных. К этому вернёмся чуть позже.

Шаг 2 — масштабируем

Мы определили нужные величины смещения для всех признаков. Теперь нужно сделать признаки сравнимыми между собой.

Степень возможного влияния признаков определяется величиной их диапазонов после масштабирования. Если оба признака распределены в одинаковых интервалах, например, [-1..1], то и влиять они могут одинаково. Если же изначально один из признаков лежит в диапазоне [-1..1], а второй — в [-1..100], то очевидно, что изменения второго могут оказывать существенно большее влияние. А значит он будет в привилегированном положении по сравнению с первым.

Стандартное отклонение

Вернёмся к примеру стандартизации. В её случае новый диапазон определяется величиной стандартного отклонения. Чем оно меньше, тем диапазон станет “шире”.

Посмотрим на гипотетические распределения различных признаков с одинаковыми начальными диапазонами (так будет нагляднее):

Для второго признака (бимодальное распределение) стандартное отклонение будет больше, чем у первого.

А это значит, что у второго признака новый диапазон после масштабирования (стандартизации) будет “уже”, и его влияние будет меньше по сравнению с первым.

Итог — стандартное отклонение не удовлетворяет начальным требованиям по одинаковому влиянию признаков (величине интервала). Даже не говоря о том, что и наличие выбросов может исказить “истинную” величину стандартного отклонения.

Межквартильный интервал

Другим часто используемым кандидатом является разница между 75-м и 25-м процентилями данных — межквартильный интервал. Т.е. интервал, в котором находятся “центральные” 50% данных набора. Эта величина уже устойчива к выбросам и не зависит от “нормальности” распределения наличия/отсутствия асимметрии.

Но и у неё есть свой серьезный недостаток — если у распределения признака есть значимый “хвост”, то после нормализации с использованием межквартильного интервала он добавит “значимости” этому признаку в сравнении с остальными.

Проблема № 2 — большие “хвосты” распределений признаков.

Пример — два признака с нормальным и экспоненциальным распределениями. Интервалы значений одинаковы

После нормализации с использованием межквартильного интервала (для наглядности оба интервала смещены к минимальным значениям равным нулю).

В итоге интервал у признака с экспоненциальным распределением из-за большого “хвоста” стал больше. А, следовательно, и сам признак стал “влиятельнее”.

Размах значений

Очевидным решением проблемы межквартильного интервала выглядит просто взять размах значений признака. Т.е. разницу между максимальным и минимальным значениями. В этом случае все новые диапазоны будут одинаковыми — равными 1.

И здесь максимально проявляется, наверное, самая частая проблема в подготовке данных, проблема № 3 — выбросы. Присутствие одного или нескольких аномальных (существенно удалённых) значений за пределами диапазона основных элементов набора может ощутимо повлиять на его среднее арифметическое значение и фиктивно увеличить его размах.

Это, пожалуй, самый наглядный пример из всех. К уже использовавшемуся выше набору из 2-х признаков добавим немного выбросов для одного признака

После нормализации по размаху

Наличие выброса, который вдвое увеличил размах признака, привело к такому же уменьшению значимого интервала его значений после нормализации. Следовательно влияние этого признака уменьшилось.

Работаем с выбросами

Решением проблемы влияния выбросов при использовании размаха является его замена на интервал, в котором будут располагаться “не-выбросы”. И дальше — масштабировать по этому интервалу.

Искать и удалять выбросы вручную — неблагодарное дело, особенно когда количество признаков ощутимо велико. А иногда выбросы и вовсе нельзя удалять, поскольку это приведёт к потере информации об исследуемых объектах. Вдруг, это не ошибка в данных, а некое аномальное явление, которое нужно зафиксировать на будущее, а не отбрасывать без изучения? Такая ситуация может возникнуть при кластеризации.

Пожалуй, самым массово применяемым методом автоматического определения выбросов является межквартильный метод. Его суть заключается в том, что выбросами “назначаются” данные, которые более чем в 1,5 межквартильных диапазонах (IQR) ниже первого квартиля или выше третьего квартиля.*

* — в некоторых случаях (очень большие выборки и др.) вместо 1,5 используют значение 3 — для определения только экстремальных выбросов.

Схематично метод изображен на рисунке снизу.

Вроде бы все отлично — наконец-то есть инструмент, и можно приступать к работе.

Но и здесь есть своя ложка дёгтя. В случае наличия длинных хвостов (как, например, при экспоненциальном распределении) слишком много данных попадают в такие “выбросы” — иногда достигая значений более 7%. Избирательное использование других коэффициентов (3 * IQR) опять приводит к необходимости ручного вмешательства — не для каждого признака есть такая необходимость. Их потребуется по отдельности изучать и подбирать коэффициенты. Т.е. универсальный инструмент опять не получается.

Ещё одной существенной проблемой является то, что этот метод симметричный. Полученный “интервал доверия” (1,5 * IQR) одинаков как для малых, так и для больших значений признака. Если распределение не симметричное, то многие аномалии-выбросы с “короткой” стороны просто будут скрыты этим интервалом.

Скорректированный интервал

Красивое решение этих проблем предложили Миа Хаберт и Елена Вандервирен (Mia Hubert and Ellen Vandervieren) в 2007 г. в статье “An Adjusted Boxplot for Skewed Distributions”.

Их идея заключается в вычислении границ “интервал доверия” с учетом асимметрии распределения, но чтобы для симметричного случая он был равен всё тому же 1,5 * IQR.

Для определения некоего “коэффициента асимметрии” они использовали функцию medcouple (MC), которая определяется так:

Поиск подходящей формулы для определения границ “интервала доверия” производился с целью сделать долю, приходящуюся на выбросы, не превышающей такую же, как у нормального распределения и 1,5 * IQR — приблизительно 0,7%

В конечном итоге они получили такой результат:

Для = 0$» data-tex=»inline»/>:

Для :

Более подробно про этот метод и его эффективность лучше прочитать в самой статье. Найти ее по названию не составляет труда.

Универсальный инструмент

Теперь, объединяя все найденные плюсы и учитывая проблемы, мы получаем оптимальное решение:

Назовем его методом… скорректированного интервала — по названию статьи Mia Hubert и Ellen Vandervieren

Теперь сравним результаты обычных методов с новым. Для примера возьмем уже использовавшиеся выше три распределения с добавлением выбросов.

Сравнивать новый инструмент будем с методами стандартизации, робастной нормализации (межквартильный интервал) и минимакса (MinMax — с помощью размаха).

Ситуация № 1 — данные необходимо центрировать. Это используется в кластеризации и многих методах машинного обучения. Особенно, когда необходимо определять меру “близости” объектов.

Робастная нормализация (по межквартильному интервалу):

Преимущество использования метода скорректированного интервала в том, что каждый из признаков равен по своему возможному влиянию — величина интервала, за пределами которого находятся выбросы, одинакова у каждого из них.

Ситуация № 2 — данные необходимо вписать в заданный интервал. Обычно это [0..1]. Это используется, например, при подготовке данных для входов нейронной сети.

В этом случае метод скорректированного интервала вписал в нужный диапазон только значения без выбросов. Значения-выбросы, выходящие за границы этого диапазона, в зависимости от постановки задачи можно удалить или принудительно приравнять ближайшей границе нужного диапазона — т.е. 0 или 1.

То, что только “нормальные” данные попадают в единичный диапазон [0..1], а выбросы не удаляются, но пропорционально выносятся за его пределы — это крайне полезное свойство, которое сильно поможет при кластеризации объектов со смешанными признаками, как числовыми, так и категорийными. Подробно об этом я напишу в другой статье.

Напоследок, для возможности пощупать руками этот метод, Вы можете попробовать демонстрационный класс AdjustedScaler из моей библиотеки AdjDataTools.

Он не оптимизирован под работу с очень большим объемом данных и работает только с pandas DataFrame, но для пробы, экспериментов или даже заготовки под что-то более серьезное вполне подойдет. Пробуйте.

Источник

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник