Что значит минимальное число
В этой статье вы узнаете, как использовать функцию МИН в Excel 2007-2019, найти минимальное значение, наименьшее значение по условию и выделить самое маленькое число в вашем диапазоне.
Сегодня мы расскажем вам, как использовать базовую, но очень важную функцию МИН в Excel. Вы увидите способы найти минимальное значение, в том числе исключая нули, абсолютный минимум и наименьшее значение с учётом условий. Кроме того, я покажу вам пошагово, как выделить цветом наименьшее число, а также подскажу, что делать, если ваша функция МИН возвращает ошибку вместо нужного результата.
Функция МИН проверяет ваш диапазон данных и возвращает минимальное значение в этом наборе.
Синтаксис для Excel МИН следующий:
Функция МИН является одной из самых простых в применении. Вот пару примеров, доказывающих это:
1. Нахождение наименьшего значения
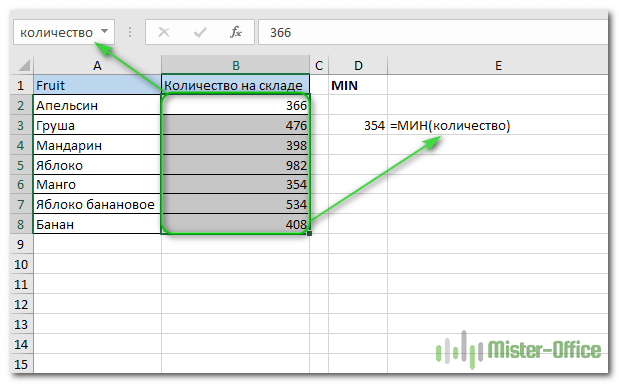
1: Ввести каждое значение из столбца «Количество на складе» в формулу:
2: Сделать ссылки на каждую ячейку столбца Количество:
3: Или просто сослаться на весь диапазон ячеек:
4: в качестве альтернативы вы можете создать именованный диапазон и использовать его вместо этого, чтобы избежать любых прямых ссылок:
2. Как найти самую раннюю дату
Представьте, что вы ждете несколько доставок и хотели бы быть готовыми к самой ближайшей. Как узнать самую раннюю дату в Excel? Легко! Используйте функцию МИН, следуя логике из примера 1:
Примените МИН и выберите даты, ссылаясь непосредственно на ячейки:
или на именованный диапазон:
3. Поиск абсолютного минимума в Excel
Предположим, что у вас есть диапазон чисел, и вам нужно определить не просто самое маленькое из них, но найти абсолютный минимум или минимум по абсолютному значению (по модулю). Одна только МИН функция не сможет справиться с этим, поскольку она просто будет искать минимальное число. Здесь вам нужна вспомогательная функция, которая может конвертировать все отрицательные числа в положительные.
Есть ли готовое решение для этого случая? Вопрос был риторическим, в Excel есть решение любой задачи. Если у вас есть какие-либо сомнения, просто просмотрите наш блог. 🙂
Но вернемся к нашей задаче. Готовое решение для этого конкретного случая называется функцией ABS, которая возвращает абсолютное значение заданных вами чисел. Таким образом, комбинация функций МИН и ABS сделает свое дело. Просто введите следующую формулу в любую пустую ячейку:
Как найти самое маленькое значение в Excel, исключая нули
Вам кажется, что вы уже знаете все о поиске минимальных значений в Excel? Не спешите с выводами, всегда есть чему поучиться. Например, как бы вы определили наименьшее ненулевое значение? Есть идеи? Не обманывай и не гугли, просто продолжай читать;)
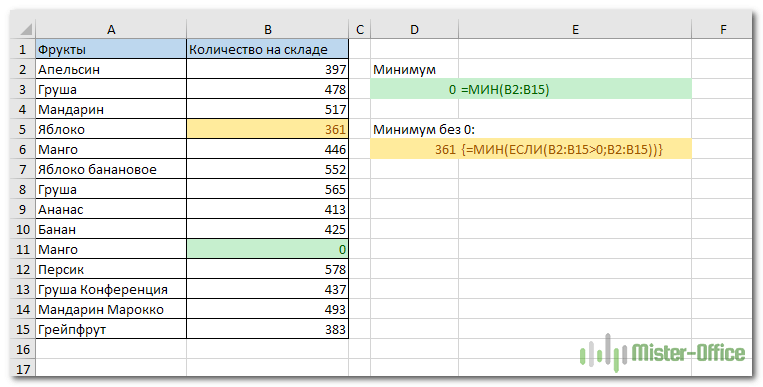
Дело в том, что Excel МИН работает не только с положительными и отрицательными числами, но и с нулями. Если вы не хотите, чтобы нули были таким минимумом, вам нужна помощь функции ЕСЛИ (IF). Как только вы добавите ограничение, что ваш диапазон должен быть больше нуля, ожидаемый результат не заставит себя ждать. Вот пример формулы для использования:
Вы, наверное, заметили фигурные скобки вокруг формулы массива. Просто помните, что вы не вводите их вручную. Они появляются в тот момент, когда вы нажимаете Ctrl + Shift + Enter на клавиатуре.
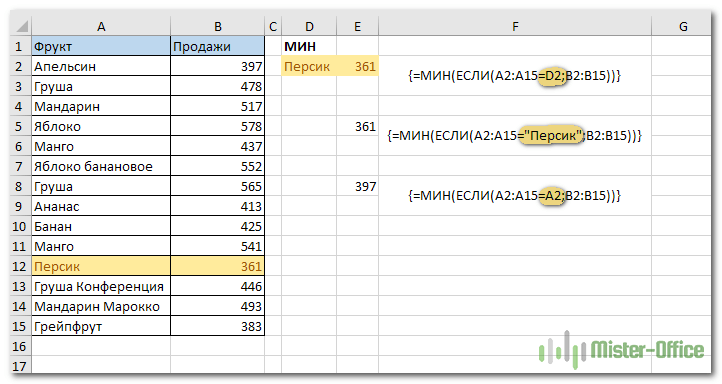
Нахождение минимума на основе условия
Нажмите Ctrl + Shift + Enter, чтобы эта функция массива работала, и наслаждайтесь результатом.
Выглядит довольно легко, правда? И как вы определите минимум на основе 2 или более условий? Может быть, есть более простая формула для этой задачи, доступная в Excel? Читайте дальше, чтобы узнать ответ. 😉
Как подсветить наименьшее число в Excel
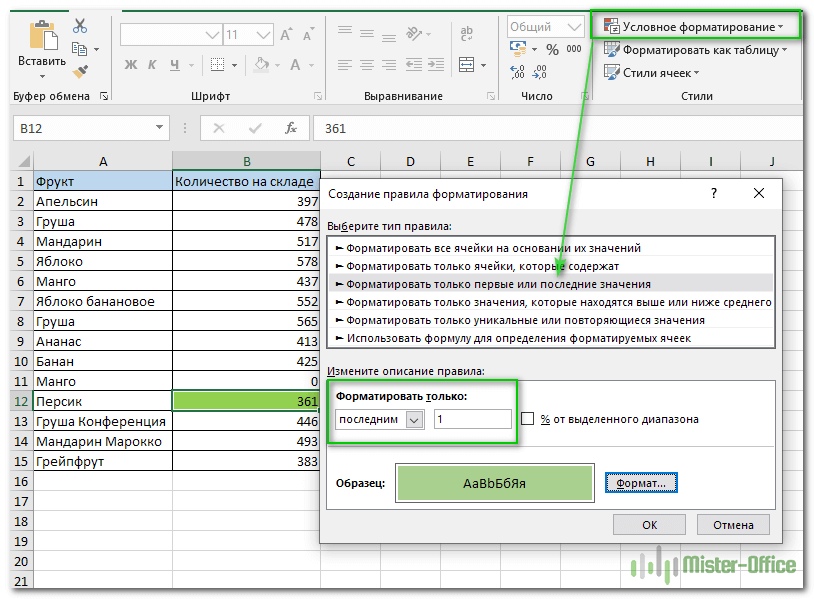
2 Когда откроется диалоговое окно «Создание правила форматирования», выберите тип правила «Форматировать только первые или последние значения».
3 Поскольку задача состоит в том, чтобы найти одно-единственное наименьшее значение, выберите опцию «последним» в раскрывающемся списке и укажите 1 в качестве количества ячеек, которые нужно выделить.
Но что делать, если в вашей таблице снова есть ноль? Как игнорировать нули при выделении минимального значения? Не беспокойтесь, для этого случая тоже есть маленькая хитрость:
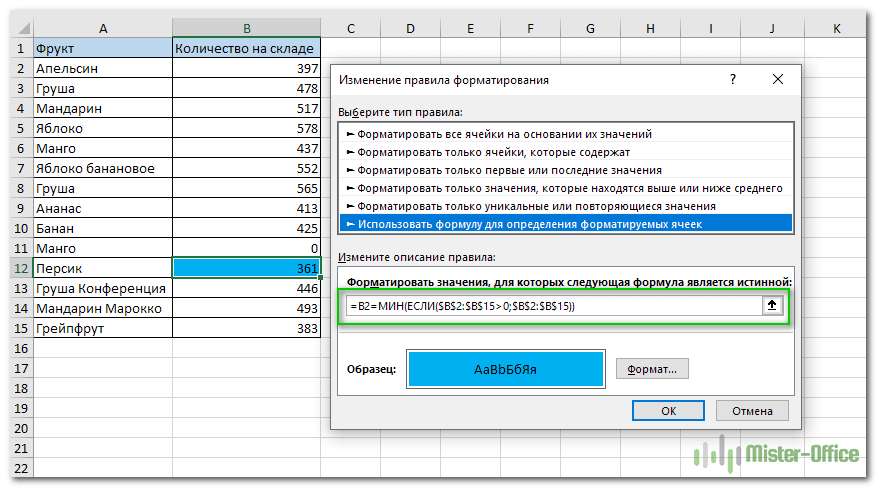
1. Создайте новое правило условного форматирования, выбрав опцию «Использовать формулу для определения форматируемых ячеек».
2. Введите это выражение в поле «Значения формата» для проверки условия:
Почему не работает функция МИН?
Исправление ошибки #ЗНАЧ! в формуле МИН
Как правило, вы получаете #ЗНАЧ! сообщение об ошибке, когда хотя бы одно из значений, использованных в формуле, неверно. Что касается МИН, это может произойти, когда один из аргументов поврежден, например, что-то не так с ячейками, которые использует формула.
Например, #ЗНАЧ! может появиться, если один из аргументов является ячейкой с ошибкой или в ссылке на ячейку есть опечатка.
Я получаю сообщение #ДЕЛ/0!, что делать?
Ищете минимум, но получаете #ИМЯ?
Другая возможная причина этой проблемы лежит в именованном диапазоне. Итак, если вы ссылаетесь на несуществующий диапазон или в нем есть опечатка, вы увидите #ИМЯ? в ячейке с результатом.
Это были некоторые из способов найти минимум в Microsoft Excel с помощью функции МИН. Для вас я рассмотрел различные подходы, чтобы найти самое маленькое значение в Excel и найти абсолютный минимум. Вы можете считать эту статью своей шпаргалкой и использовать всякий раз, когда вам нужно найти минимальное число в зависимости от условия, чтобы предотвратить и исправить возможные ошибки.
Вот и все на сегодня. Пожалуйста, не стесняйтесь делиться своими мыслями и вопросами в разделе комментариев, я буду рад получить от вас обратную связь! 🙂
Что такое максимум и минимум?
Что такое максимум и минимум?
— Получать максимум от общения.
— Чтобы выучить стихотворение его нужно прочесть как минимум 3-4 раза.
— Максимум на что он способен, это…..
— У них есть как минимум два общих друга.
— Он получил максимальный бал.
— Используй возможности по-максимуму!
— Это тот минимум, который нужно знать.
— Минимальное атмосферное давление.
— Минимальные/максимальные холода за ….. лет.
— Вам потребуется минимум несколько часов для выполнения этой работы.
Такие понятия как максимум и минимум можно встретить и в специальных научных терминах. Например, в математике есть такое понятие как максимум и минимум функции.
Таким образом, максимумом в математике называется наибольшее значение функции. При этом максимальное значение функции больше всех соседних с ней значений. Максимум функции – это такое ее значение, когда сначала значение увеличивается, а затем сразу же начинает убывать, при этом она имеет максимум в том месте, где увеличение и уменьшение функции переходят от одного к другому. Минимум функции – это, соответственно, наименьшее значение функции.
Первую производную функции можно считать положительной, если она поднимается вверх, когда мы увеличиваем переменную, тогда функцию можно считать положительной. Если же первая переменная при увеличении производного, убывает, то функцию следует считать отрицательной.
Производная – это основное значение, которое используют при дифференциальных вычислениях (изучение производной и дифференциала, которые помогают исследовать математические функции), она может пониматься как скорость изменения функции в конкретной точке. Чем скорость больше, тем сильнее меняется функция, чем меньше, тем медленнее (это, однако, правда, только если функция положительная). Таким образом, именно скорость изменения функции в заданной точке и определяет ее наклоны и выпуклости. А переменная – это величина, которая способна менять свое значение. Ее обозначают как x или time.
Переменной можно считать атрибут системы (как физической, так и абстрактной), который способен изменить свое значение. В более глобальном смысле переменной можно назвать и время, и температуру и, вообще, всю жизнь (они могут меняться). Переменная имеет множество значений, которые она способна принимать. Можно считать, что это множество и является переменной.
Что касается непосредственно функции, то она должна пройти от положительного к отрицательному значению через ноль. Таким образом, при том значении переменного, которому соответствует максимум функции, ее производная будет равна нулю. Именно это свойство функции позволяет определять значения x, при которых функция достигает максимума. Однако, если мы увеличим переменную и, при этом, функция сначала увеличивается, а затем уменьшается, то функция, при изменении с отрицательного значения на положительное (пройдя через ноль), достигнет не максимального, а, наоборот, минимального значения. Хотя по логике вещей это можно было бы принять именно за максимальное значение (он находится в верхней точке функции).
Точки максимума и минимума функции еще называют точками экстремума.
Таким образом, как в обычной жизни, так и в математике максимум и минимум – это две крайние противоположности, которые обозначают что-то самое большое и что-то самое маленькое.
Какие числа называются целыми
Определение целых чисел
Что важно знать о целых числах:
Целые числа на числовой оси выглядят так:
На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.
В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.
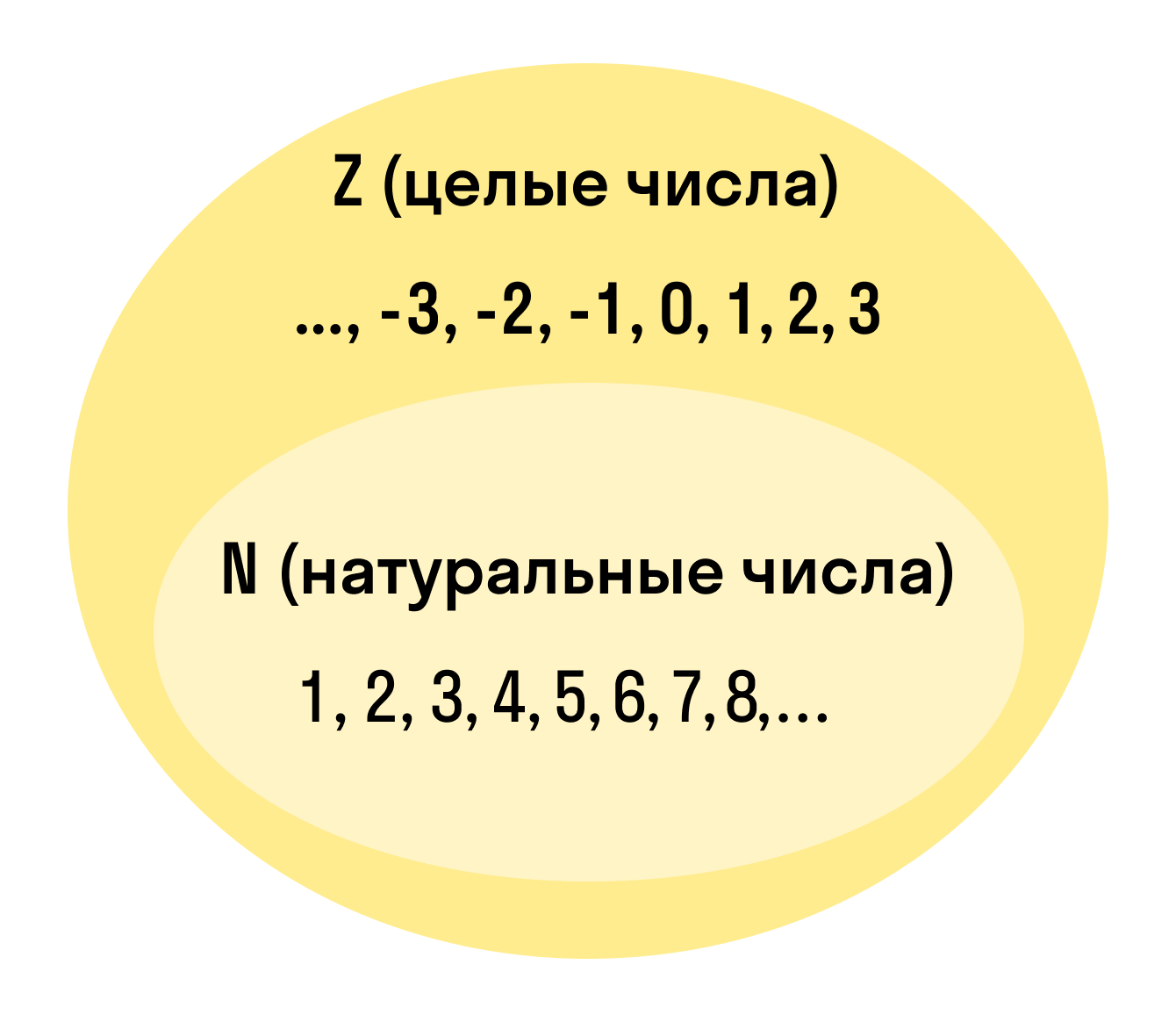
Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.
Выглядит эти ребята вот так:
Последовательность целых чисел можно записать так:
Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:
Простые числа — это чудеса деления
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком математическом понятии, как ПРОСТЫЕ ЧИСЛА.
В школе это проходят в 5 или 6 классе, в зависимости от программы обучения.
И интересно, что если спросить школьников, что такое простые числа, то они, скорее всего, ответят правильно.
А вот взрослые задумаются и не факт, что вспомнят точное определение. Так что это статья скорее для них.
Простые числа — это.
Итак, вот как выглядит официальное определение:
Простые числа – это такие числа, которые имеют только два делителя. Один из них – единица, а другое – само число.
Чтобы было более понятно, приведем простой пример. Для чисел 5 и 7 надо найти все возможные делители, чтобы в результате образовалось целое число.
Если вы попробуете решить эту задачку, то получите, что 5 и 7 делятся только на 1 и 5, и 1 и 7 соответственно. Во всех других случаях вы получите дробное число. И это как раз означает, что числа 5 и 7 относятся к простым.
А вот попробуем по той же схеме разобрать числа 6 и 9. В первом случае мы получим, что 6 можно поделить на 1, 2, 3 и 6, а число 9 – на 1, 3 и 9. И это уже противоречит определению простых чисел, значит, 6 и 9 таковыми не являются.
Они называются в математике – СОСТАВНЫМИ ЧИСЛАМИ.
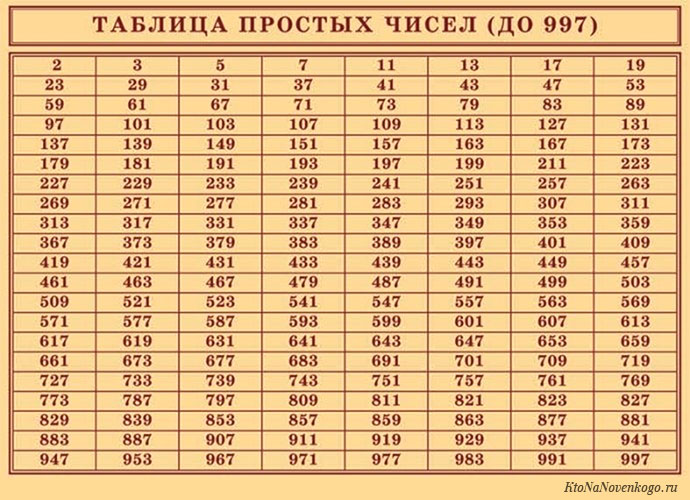
Список и таблица простых чисел
Некоторые ошибочно полагают, что наименьшее простое число – это единица.
С одной стороны, в этом есть логика, так как 1 делится только на 1. Но это получается одно и то же число (единица), что противоречит определению простых чисел, в котором четко прописано – «делителей должно быть два».
Значит, минимальное простое число – это 2. А первоначальный ряд выглядит следующим образом:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199…
При желании можете проверить эти числа на предмет деления. Мы же скажем, что этот ряд на самом деле не окончательный.
Количество простых чисел не ограничено. Или говоря математическим языком, оно стремится к бесконечности.
История простых чисел
Первые упоминания о простых числах относятся к Древнему Египту. В Британском музее хранится папирус, который датируется 2000 годом до нашей эры. И на нем, согласно расшифровке, содержится учебное пособие по арифметике.
В том числе и про деление чисел. Называется этот артефакт – папирус Райнда, по имени его первого владельца.
В этом документе есть таблица, в которой указаны числа, делящиеся на различные знаменатели. Причем они разделены таким образом, что становится понятно – древние египтяне может и не пользовались понятиям «простое число», но хотя бы имели о нем представление.
Ну а первые исследования простых чисел датируются 300 годом до нашей эры. И связаны они с именем знаменитого древнегреческого математика Евклида.
Как и многое другое, он описал простые и составные числа в своем известном произведении «Начала».
В частности, Евклид описал такие вещи, как:
Сейчас расскажем об этих понятиях подробнее.
Основная теорема арифметики
Основная теорема арифметики, которую придумал еще Евклид, гласит:
Любое натуральное число (это что?), которое больше единицы, может быть представлено в виде произведения простых чисел. Причем их количество не ограничено, а порядок следования неважен.
Если обозначить исходное число буквой N, а простые числа буквами Р1, Р2, Р3 и так далее, то можно записать эту теорему следующим образом:
N = Р1 * Р2 * Р3 * … * РК
Например, возьмем число 100. Его можно разложить на следующие простые числа:
Или более сложный пример – число 23244:
23244 = 149 * 13 * 3 * 2 * 2
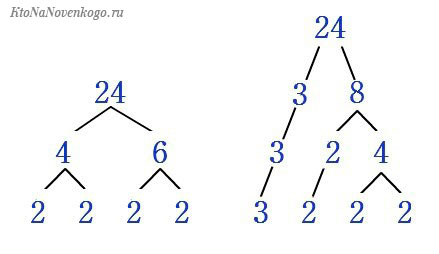
Раскладывать на простые числа легко. Можно сперва делить на 2 и 3, а уже в конце автоматически получить более сложные делители.
Ради интереса придумайте любое число и сами найдите его составляющие.
Лемма Евклида
Еще одна теорема, которая имеет прямое отношение к простым числам. Она гласит;
Если некое простое число Р делит произведение чисел X и Y без остатка, то оно может точно так же поделить или X, или Y.
Звучит несколько сложновато, хотя на деле все это просто. Так, возьмем для примера P = 2, X = 6, Y = 9. И тогда получается, что
В нашем примере P делит это произведение без остатка:
А значит наша P может поделить без остатка или X, или Y. Очевидно, что это X:
Y/P = 9/2 = 4,5 (не подходит)
Как быстро и легко определить простые числа
И еще одно понятие, которое связано с простыми числами. Оно названо в честь другого древнегреческого математика Эратосфена Киренского.
Этот человек придумал, как быстро и легко определить простые числа. В частности, он сделал таблицу, в которой были указаны значения до 1000.
Свою таблицу он нарисовал на глиняной дощечке. А после прокалывал те клеточки, на которых были написаны составные числа. В результате получилось нечто вроде решета, отсюда собственно и название метода.
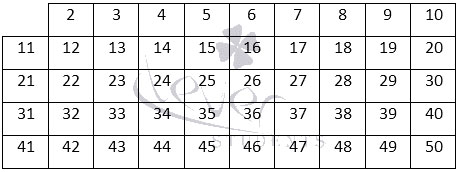
Кстати, пользоваться решетом Эратосфена весьма просто. Например, сделаем таблицу до 50.
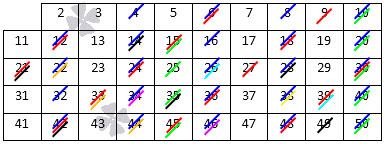
После этого из нее надо поочередно вычеркивать числа, которые кратны 2, 3, 5, 7 и 11. В результате получится вот это:
Те числа, которые остались, и есть простые. Можете сравнить этот ряд с тем, который мы давали в начале статьи. Точно таким же способом можно составить абсолютно любой ряд простых чисел = хоть до тысячи, хоть до миллиона и больше.
Вот и все, что мы хотели рассказать о ПРОСТЫХ ЧИСЛАХ в математике.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Математика весьма хитрая наука, да и простые числа не такие уж и простые, понимание простых и составных чисел привело человечество к тому техническому прогрессу, что окружает нас сейчас.
Минимум – что означает? Определение, значение, примеры употребления
Ищешь, что значит слово минимум? Пытаешься разобраться, что такое минимум? Вот ответ на твой вопрос:
Значение слова «минимум» в словарях русского языка
Минимум это:
минимум — это наименьшее возможное количество чего-либо в данном контексте.
Минимум
1.Наименьшее количество чего-либо; наименьшая величина. Ant:максимум I
2.Минимальная совокупность чего-либо необходимого.
3.Система принудительной таксации цен или заработной платы. II м. разг.
1.Совокупность знаний, обязательных для специалиста.
2.Экзамены для определения уровня таких знаний. III нареч. качеств.-количеств. разг.Самое меньшее; не меньше чего-либо.
Минимум
( лат. minimum наименьшее)
1) наименьшая величина; наименьшее количество; низшая степень чего-л.;
2) мат. наименьшее значение функции, принимаемое в нек-рой точке независимого переменного по сравнению с другими значениями этой функции.
Минимум
1. м.
1) Наименьшее количество чего-л.; наименьшая величина (противоп.: максимум).
2) Минимальная совокупность чего-л. необходимого.
3) а) разг. Совокупность знаний, обязательных для специалиста. б) Экзамены для определения уровня таких знаний.
2. нареч. разг. По меньшей мере, самое меньшее.
Минимум
Минимум
1. наименьшая величина; наименьшее количество; низшая степень чего-л.;
2. мат. наименьшее значение функции, принимаемое в нек-рой точке независимого переменного по сравнению с другими значениями этой функции.
Минимум
Минимум
-а,м. минимальное, наименьшее количество, наименьшая вели&на в ряду данных максимум М. затрат. Прожиточный м. (средства, необходимые для существования, для того, чтобы прожить, для поддержания трудоспособности).
Минимум
Минимум
1. м.
1) Наименьшее количество чего-л.; наименьшая величина (противоп.: максимум).
2) Минимальная совокупность чего-л. необходимого.
3) а) разг. Совокупность знаний, обязательных для специалиста. б) Экзамены для определения уровня таких знаний.
2. нареч. разг. По меньшей мере, самое меньшее.
Минимум
минимума, м. (латин. minimum) (книжн.).
1. Наименьшая величина; противоп. максимум. Минимум атмосферного давления. Минимум заработной платы. Прожиточный минимум (минимум средств, денег, необходимый для прожития; экон.).
2. в знач. нареч. Самое меньшее, не меньше чего-н.; то же, что минимально во 2 знач. (разг.). Эта работа потребует для своего выполнения минимум два дня.
3. в знач. неизмен. прил. (ставится после определяемого слова). То же, что минимальный (книжн.). Программа-минимум.
Минимум
Минимум
Минимум
Минимум
наименьшее значение какой-либо величины наименьшее значение функции на заданном множестве самое малое, не меньше
Где и как употребляется слово «минимум»?
Кроме значения слова «минимум» в словарях, рекомендуем также ознакомиться с примерами предложений и цитат из классической литературы, в которых употребляется слово «минимум».
Так вы сможете гораздо легче понять и запомнить, как правильно употребляется слово «минимум» в тексте и устной речи.
Примеры употребления слова «минимум»
– Судя по всему, нам придётся терпеть друг друга ещё минимум две недели, – сказал я коту, когда мы отправились в обратный путь.
А значит, ради гребанных 2 единиц генома мне ещё минимум три часа носиться с полным брюхом туда-сюда.
Правда, её нынешние обитатели одним своим видом привели бы в ужас любого туриста, но туристы не появлялись в окрестностях базы уже как минимум лет десять.