Что значит логарифмическая сложность
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
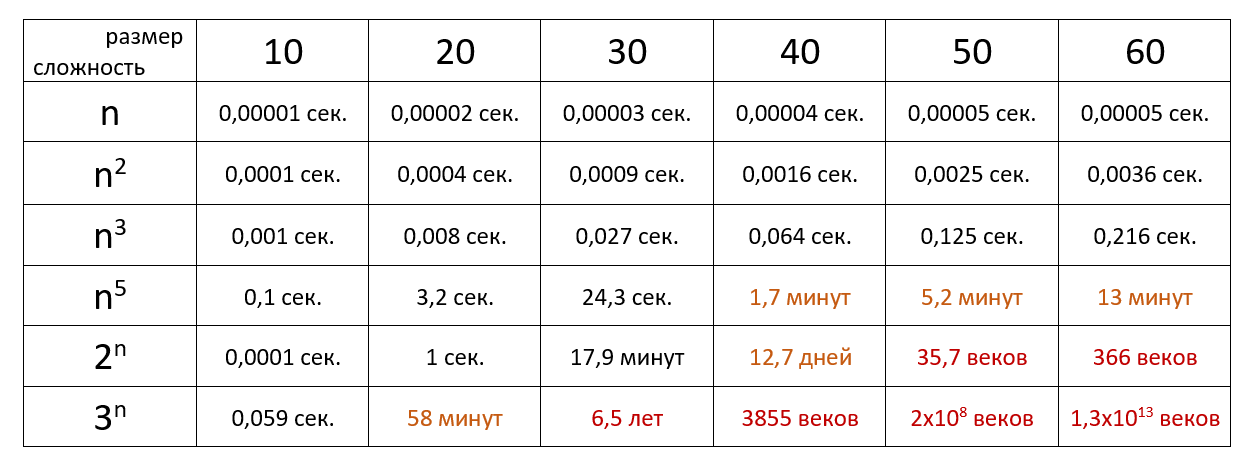
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
Введение в анализ сложности алгоритмов (часть 3)
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.
Логарифмы
Практическая рекомендация: на соревнованиях алгоритмы часто реализуются на С++. Как только вы проанализировали сложность вашего алгоритма, так сразу можете получить и грубую оценку того, как быстро он будет работать, приняв, что в секунду выполняется 1 000 000 команд. Их количество считается из полученной вами функции асимптотической оценки, описывающей алгоритм. Например, вычисление по алгоритму с Θ( n ) займёт около секунды при n = 1 000 000.
Рекурсивная сложность
Если вы всё же не уверены в этом, то вы всегда можете найти точную сложность путём подсчёта количества инструкций. Примените этот метод к данной функции, чтобы найти её f( n ), и убедитесь, что она линейная (напомню, что линейность означает Θ( n ) ).
Логарифмическая сложность
Одной из известнейших задач в информатике является поиск значения в массиве. Мы уже решали её ранее для общего случая. Задача становится интереснее, если у нас есть отсортированный массив, в котором мы хотим найти заданное значение. Одним из способов сделать это является бинарный поиск. Мы берём средний элемент из нашего массива: если он совпадает с тем, что мы искали, то задача решена. В противном случае, если заданное значение больше этого элемента, то мы знаем, что оно должно лежать в правой части массива. А если меньше — то в левой. Мы будем разбивать эти подмассивы до тех пор, пока не получим искомое. 
Вот реализация такого метода в псевдокоде:
Если вы не уверены, что метод работает в принципе, то отвлекитесь и решите вручную какой-нибудь простой пример.
Если вы прочли раздел о логарифмах выше, то такое выражение будет для вас знакомым. Решив его, мы получим:
Практическая рекомендация: улучшение асимптотического времени выполнения программы часто чрезвычайно повышает её производительность. Намного сильнее, чем небольшая «техническая» оптимизация в виде использования более быстрого языка программирования.
Оценка сложности алгоритмов
Введение
Для любого программиста важно знать основы теории алгоритмов, так как именно эта наука изучает общие характеристики алгоритмов и формальные модели их представления. Ещё с уроков информатики нас учат составлять блок-схемы, что, в последствии, помогает при написании более сложных задач, чем в школе. Также не секрет, что практически всегда существует несколько способов решения той или иной задачи: одни предполагают затратить много времени, другие ресурсов, а третьи помогают лишь приближённо найти решение.
Всегда следует искать оптимум в соответствии с поставленной задачей, в частности, при разработке алгоритмов решения класса задач.
Важно также оценивать, как будет вести себя алгоритм при начальных значениях разного объёма и количества, какие ресурсы ему потребуются и сколько времени уйдёт на вывод конечного результата.
Этим занимается раздел теории алгоритмов – теория асимптотического анализа алгоритмов.
Предлагаю в этой статье описать основные критерии оценки и привести пример оценки простейшего алгоритма. На Хабрахабре уже есть статья про методы оценки алгоритмов, но она ориентирована, в основном, на учащихся лицеев. Данную публикацию можно считать углублением той статьи.
Определения
Основным показателем сложности алгоритма является время, необходимое для решения задачи и объём требуемой памяти.
Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объём данных – размер входа.
Итак, можем сделать вывод, что сложность алгоритма – функция размера входа.
Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.
Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.
Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.
Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.
Порядок роста сложности алгоритмов
Порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.
Шаг алгоритма – совокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.
Виды асимптотических оценок
O – оценка для худшего случая
Рассмотрим сложность f(n) > 0, функцию того же порядка g(n) > 0, размер входа n > 0.
Если f(n) = O(g(n)) и существуют константы c > 0, n0 > 0, то
0 n0.
Функция g(n) в данном случае асимптотически-точная оценка f(n). Если f(n) – функция сложности алгоритма, то порядок сложности определяется как f(n) – O(g(n)).
Данное выражение определяет класс функций, которые растут не быстрее, чем g(n) с точностью до константного множителя.
Примеры асимптотических функций
| f(n) | g(n) |
|---|---|
| 2n 2 + 7n — 3 | n 2 |
| 98n*ln(n) | n*ln(n) |
| 5n + 2 | n |
| 8 | 1 |
Ω – оценка для лучшего случая
Критерии оценки сложности алгоритмов
Равномерный весовой критерий (РВК) предполагает, что каждый шаг алгоритма выполняется за одну единицу времени, а ячейка памяти за одну единицу объёма (с точностью до константы).
Логарифмический весовой критерий (ЛВК) учитывает размер операнда, который обрабатывается той или иной операцией и значения, хранимого в ячейке памяти.
Временная сложность при ЛВК определяется значением l(Op), где Op – величина операнда.
Ёмкостная сложность при ЛВК определяется значением l(M), где M – величина ячейки памяти.
Пример оценки сложности при вычислении факториала
Необходимо проанализировать сложность алгоритма вычисление факториала. Для этого напишем на псевдокоде языка С данную задачу:
Временная сложность при равномерном весовом критерии
Достаточно просто определить, что размер входа данной задачи – n.
Количество шагов – (n — 1).
Таким образом, временная сложность при РВК равна O(n).
Временная сложность при логарифмическом весовом критерии
В данном пункте следует выделить операции, которые необходимо оценить. Во-первых, это операции сравнения. Во-вторых, операции изменения переменных (сложение, умножение). Операции присваивания не учитываются, так как предполагается, что она происходят мгновенно.
Итак, в данной задаче выделяется три операции:
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы так и не понимаете, что это значит, — эта статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n2) — квадратичная сложность
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10⁶ операций в секунду:
Тут можно посмотреть сложность основных алгоритмов сортировки и работы с данными.