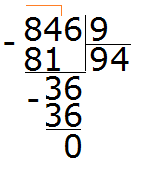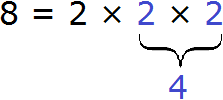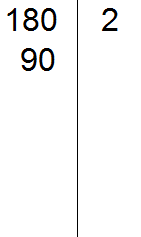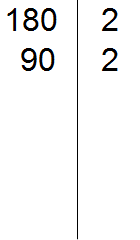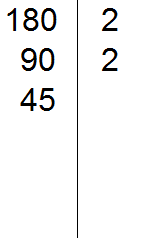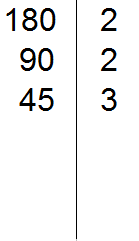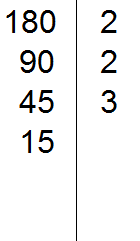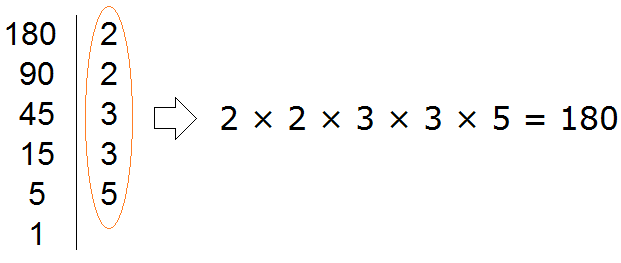Что значит кратен 400

Что такое кратное число

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.

Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.

Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.

Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.

Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).

А у чисел, которые участвуют в делении, есть определенные названия:

Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.

Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.

Одно число называется кратным другому, если его можно на него поделить без остатка.

Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.

Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.

12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6

Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.

Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:

Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.

Таблицы чисел кратных 2,3,4,5,6,7,9

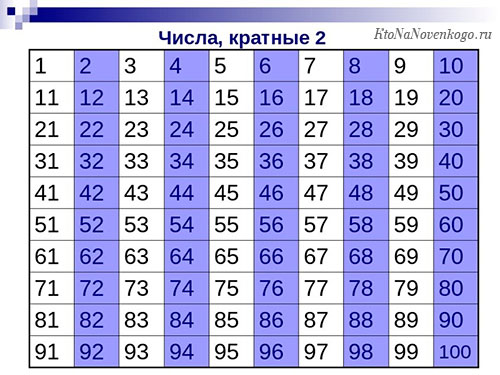
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.

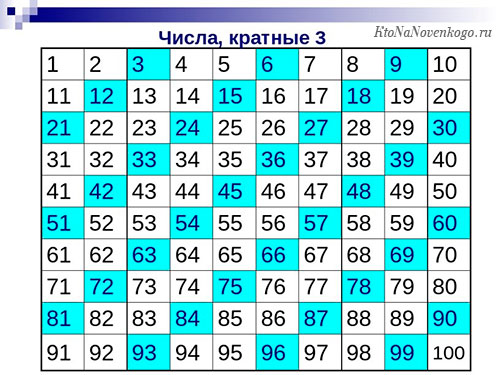
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.

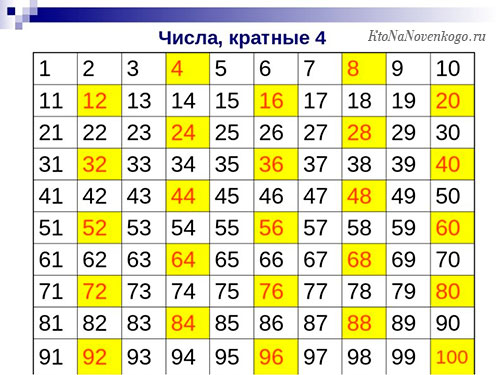
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.

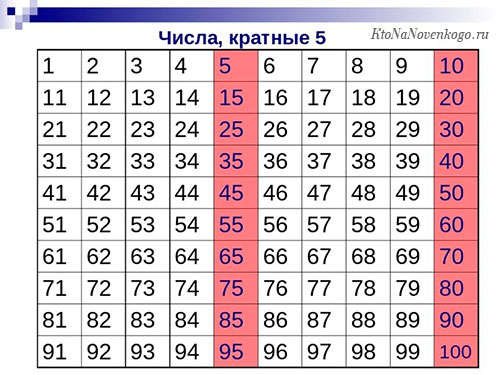
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.

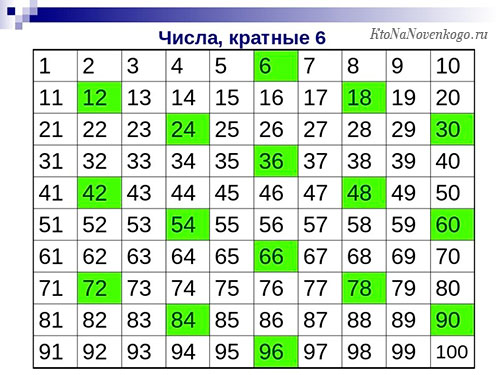
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.

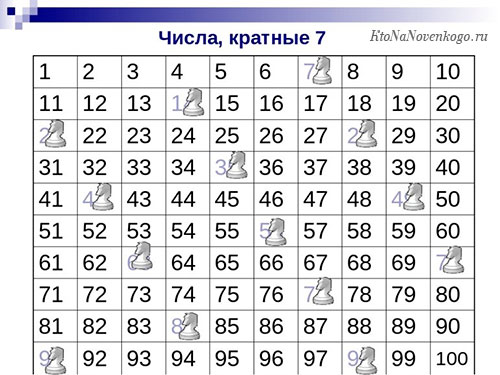
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».

И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.

Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.

Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.

Вместо заключения

А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.

Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.

Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.

Источник

Високосные годы

Надеюсь, вы отлично встретили новый год, и сейчас у вас отличное праздничное настроение. По крайней мере у меня это именно так — мы не пили никакого алкоголя, и чокнулись в полночь бокалами с водой из пятилитровой канистры, поэтому мы проснулись, погуляли, и тут я вспомнил одно из вчерашних поздравлений с Новым годом:

— Ох, нифига себе, какой был экшен. Обязательно буду рассказывать внукам или напишу об этом потом книгу.

Итак, выше достаточно простой inline-способ определить количество дней в году (переменная year), который, по сути, полностью раскрывает их суть: в григорианском календаре високосными годами считаются те годы, порядковый номер которых либо кратен 4, но при этом не кратен 100, либо кратен 400. Иными словами, если год делится на 4 без остатка, но делится на 100 только с остатком, то он високосный, иначе — невисокосный, кроме случая, если он делится без остатка на 400 — тогда он всё равно високосный.

Например, 2013 год невисокосный, 1700, 1800 и 1900 — опять же невисокосные годы, а вот 2000, 2004, 2008 и 2012 — високосные.

Но что, если мы не помним, сколько дней в високосных (366 дней) и невисокосных (365 дней) годах, или просто хотим написать определение количества дней в году максимально быстро? Можно ли сделать так на Python? Конечно же, можно.

Итак, в Python есть модуль calendar. Он как раз отлично подходит для того, чтобы узнать, является ли тот или иной год високосным (или, например, сколько високосных годов в определённом интервале), определить количество дней в месяце, получить номер дня недели для определённой даты и так далее.

В частности, мы можем получить количество дней в каждом месяце года, и просто сложить.

Функция calendar.monthrange принимает номер года в качестве первого аргумента и номер месяца в качестве второго аргумента. Возвращает номер дня недели первого числа данного месяца и количество дней в данном месяце:

Соответственно, мы можем подсчитать общее количество дней для всех 12 месяцев, и получить таким образом количество дней для данного года:

Но если подумать о том, как именно выполняется эта строка, становится очевидно, что это решение очень неэффективно, если нужно посчитать количество дней для большого количества годов.

Проверяем с помощью модуля timeit.

На то, чтобы выполнить её 1 миллион раз, требуется 13.69 секунд, если import calendar делается один раз в начале. Если import calendar делается каждый раз, тогда 14.49 секунд.

Теперь попробуем другой вариант. Он требует знания того, сколько дней в високосных и невисокосных годах, но зато он очень короткий:

И, как легко догадаться, он уже намного быстрее: 0.83 секунд, включая import calendar, и 0.26 секунд, если import calendar делается один раз в начале.

Давайте также посмотрим, сколько требуется времени самому первому варианту, с «ручным» подходом: 0.07 секунд для 2012 и 2013 и 0.12 секунд для 2000 (думаю, всем понятно, откуда берётся такая разница в скорости для этих годов).

Получается, что это и есть самый быстрый вариант из этих трёх:

Конечно, в большинстве случаев вы можете использовать любой из этих вариантов — в конце концов, при определении количества дней в одном, двух, десяти или ста годах вы вряд ли почувствуете какую-либо разницу.

Пишите, оптимизируйте, улучшайте, тестируйте и считайте производительность — но не забывайте о читаемости исходников ваших программ.

С Новым годом! Удачи, счастья, радости и самосовершенствования в новом году.

Источник

КРАТНЫЙ

Смотреть что такое «КРАТНЫЙ» в других словарях:

кратный — сложный, составной; кратен. Ant. простой Словарь русских синонимов. кратный прил., кол во синонимов: 2 • аликвотный (1) • … Словарь синонимов

КРАТНЫЙ — КРАТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.). 1. Делящийся без остатка на какое нибудь число. Число десять кратно пяти и двум. 2. в знач. сущ. кратное, кратного, ср. Целое число, делящееся на данное. Десять кратное двух. Общее… … Толковый словарь Ушакова

кратный — КРАТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.). 1. Делящийся без остатка на какое нибудь число. Число десять кратно пяти и двум. 2. в знач. сущ. кратное, кратного, ср. Целое число, делящееся на данное. Десять кратное двух. Общее… … Толковый словарь Ушакова

кратный — КРАТНЫЙ, кратная, кратное; кратен, кратна, кратно (мат.). 1. Делящийся без остатка на какое нибудь число. Число десять кратно пяти и двум. 2. в знач. сущ. кратное, кратного, ср. Целое число, делящееся на данное. Десять кратное двух. Общее… … Толковый словарь Ушакова

. кратный — …КРАТНЫЙ, кратная, кратное. Вторая часть сложных прил. в знач. повторяющийся столько то раз, больший во столько то раз (сколько указывает первая часть), напр. семикратный, многократный. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

КРАТНЫЙ — КРАТНЫЙ, ая, ое; тен, тна. В математике: делящийся без остатка на какое н. число. Девятьчисло, кратное трём. Девятькратное (сущ.) трёх. | сущ. кратность, и, жен. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

кратный — кратный, кратк. ф. кратен, кратна (неправильно кратна), кратно, кратны … Словарь трудностей произношения и ударения в современном русском языке

кратный — свернутый — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы свернутый EN fold … Справочник технического переводчика

кратный — ▲ целый ↑ соотношение кратность целое соотношение. деление нацело. делимость (признаки делимости). делитель (# числа). составное число. < > простое число. кратное число число, которое делится без остатка на другое число. четный кратный двум … Идеографический словарь русского языка

кратный — 1) кратный ая, ое; тен, тна, тно. мат. 1. Делящийся без остатка на какое л. число. Кратные числа. 2. в знач. сущ. кратное, ого, ср. Целое число, делящееся на данное без остатка. 2) …кратный ая, ое. Вторая составная часть сложных слов,… … Малый академический словарь

Источник

Делители и кратные

В данном уроке мы рассмотрим такие понятия как делители и кратные.

Что такое делитель?

Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.

Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:

Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:

Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:

10 : 4 = 2 (2 в остатке)

Определение. Делителем числа а называется число, на которое число а делится без остатка.

Делителем числа 12 называется число, на которое 12 делится без остатка.

Попробуем перечислить эти числа:

Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:

12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1

Кратные числа

Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3

Определение. Кратным числа а называется число, которое делится без остатка на а.

Кратным числа 5 называется число, которое делится без остатка на 5 .

У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:

5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5

Признаки делимости чисел

Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.

Признак делимости на 10

Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.

Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.

В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.

Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.

Признак делимости на 5 и на 2

Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.

Признак делимости на 5

Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.

Признак делимости на 3

Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:

Признак делимости на 9

Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9

Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:

Чётные и нечётные числа

Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:

Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:

21 : 2 = 10 (1 в остатке)

Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.

Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.

А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.

Простые и составные числа

Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:

Значит, число 5 является простым числом.

Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1

Значит, число 4 является составным числом.

Разложение составного числа на простые множители

Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.

Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.

Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4

Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6

Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.

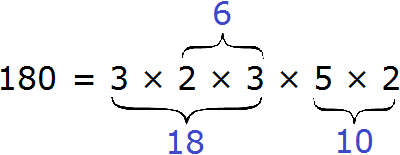
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10

Теперь раскладываем множители 18 и 10 на другие множители:

Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:

Теперь собираем все простые множители вместе:

На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.

Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.

При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.

Например, разложим предыдущее число 180 этим способом.

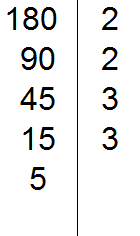
Проводим вертикальную линию и слева записываем первое делимое 180

Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.

180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:

Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.

90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:

Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:

Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.

45 на 2 не делится. Тогда проверяем делится ли 45 на 3.

45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:

Теперь делим 15. Проверяем делится ли 15 на 2.

15 не делится на 2. Тогда проверяем делится ли 15 на 3.

15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:

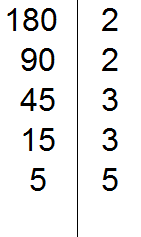
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:

Теперь делим 5. Проверяем делится ли 5 на 2.

5 не делится на 2. Тогда проверяем делится ли 5 на 3.

5 не делится на 3. Тогда проверяем делится ли 5 на 5.

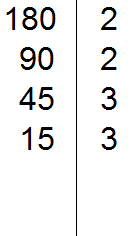
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:

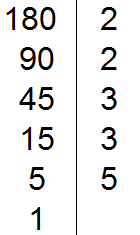
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:

На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.

Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:

Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.

Нахождение делителей числа

В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.

Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2

6 : 2 = 3

Ещё делителем числа 6 является число 3

6 : 3 = 2

Ещё делителем числа 6 является число 1

6 : 1 = 6

Наконец, делителем числа 6 является само это число

6 : 6 = 1

Перечислим все делители числа 6

1, 2, 3, 6

Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.

Пример 1. Найти делители числа 12

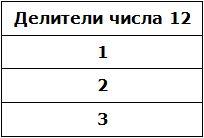
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1

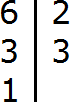
Теперь раскладываем число 12 на простые множители:

Получили разложение 2 × 2 × 3.

В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:

Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.

Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4

Занесём число 4 в нашу таблицу делителей

Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:

Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:

Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.

На основании приведённого примера можно сформировать правило для нахождения делителей числа:

Чтобы найти делители числа, нужно:

Пример 2. Найти делители числа 6

Первым делителем числа 6 запишем единицу:

Теперь разложим число 6 на простые множители:

Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:

1, 2, 3

1, 2, 3, 6

Источник