Тригонометрия и геометрия в чем разница
Тригонометрия
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
В Школе СССР имела статус учебного предмета.
Содержание
Определение тригонометрических функций
Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).
Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до 
радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол 
(если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:
Для острых углов новые определения совпадают с прежними.
Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.
История
Древняя Греция
Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.
Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β Средневековая Индия
Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
Индийцы также знали формулы для кратных углов 
, 
, где 
.
Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.
Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.
В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.
Разница между геометрией и тригонометрией
Геометрия против тригонометрии Математика имеет три основных раздела: арифметика, алгебра и геометрия. Геометрия — это исследование форм, размеров и свойств пространств определенного количества измер
Содержание:
Геометрия против тригонометрии
Математика имеет три основных раздела: арифметика, алгебра и геометрия. Геометрия — это исследование форм, размеров и свойств пространств определенного количества измерений. Великий математик Евклид внес огромный вклад в геометрию поля. Поэтому он известен как отец геометрии. Термин «геометрия» происходит от греческого языка, в котором «Гео» означает «Земля», а «метрон» означает «мера». Геометрию можно разделить на плоскую, твердую и сферическую. Плоская геометрия имеет дело с двумерными геометрическими объектами, такими как точки, линии, кривые и различные плоские фигуры, такие как круг, треугольники и многоугольники. Твердая геометрия изучает трехмерные объекты: различные многогранники, такие как сферы, кубы, призмы и пирамиды. Сферическая геометрия имеет дело с трехмерными объектами, такими как сферические треугольники и сферический многоугольник. Геометрия используется ежедневно, практически везде и всеми. Геометрию можно найти в физике, инженерии, архитектуре и многом другом. Другой способ категоризации геометрии — это евклидова геометрия, изучение плоских поверхностей, и риманова геометрия, в которой основной темой является изучение кривых поверхностей.
Тригонометрию можно рассматривать как раздел геометрии. Впервые тригонометрия была представлена примерно в 150 г. до н.э. эллинистическим математиком Гиппархом. Он составил тригонометрическую таблицу с использованием синуса. Древние общества использовали тригонометрию как метод навигации в парусном спорте. Однако тригонометрия развивалась на протяжении многих лет. В современной математике тригонометрия играет огромную роль.
Тригонометрия — это в основном изучение свойств треугольников, длин и углов. Однако он также имеет дело с волнами и колебаниями. Тригонометрия имеет множество приложений как в прикладной, так и в чистой математике, а также во многих областях науки.
В тригонометрии мы изучаем отношения между длинами сторон прямоугольного треугольника. Есть шесть тригонометрических соотношений. Три основных, называемых синусом, косинусом и тангенсом, вместе с секансом, косекансом и котангенсом.
Например, предположим, что у нас есть прямоугольный треугольник. Сторона перед прямым углом, другими словами, самое длинное основание в треугольнике, называется гипотенузой. Сторона перед любым углом называется противоположной стороной этого угла, а сторона, оставшаяся позади этого угла, называется смежной стороной. Тогда мы можем определить основные тригонометрические отношения следующим образом:
sin A = (противоположная сторона) / гипотенуза
cos A = (прилегающая сторона) / гипотенуза
tan A = (противоположная сторона) / (прилегающая сторона)
Тогда косеканс, секанс и котангенс можно определить как обратную величину синуса, косинуса и тангенса соответственно. На этой базовой концепции построено еще много тригонометрических отношений. Тригонометрия — это не только исследование плоских фигур. У него есть ветвь, называемая сферической тригонометрией, изучающая треугольники в трехмерных пространствах. Сферическая тригонометрия очень полезна в астрономии и навигации.
В чем разница между геометрией и тригонометрией?
¤ Геометрия — это главный раздел математики, а тригонометрия — это раздел геометрии.
¤ Геометрия — это исследование свойств фигур. Тригонометрия — это исследование свойств треугольников.
Тригонометрия
Тригономе́трия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561-1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии.
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Например, большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
История[править | править код]
Древняя Греция[править | править код]
Первые тригонометрические таблицы видимо были составлены Гиппархом, который сейчас известен как «отец тригонометрии»[2].
51. Планиметрия 
Читать 0 мин.
Читать 0 мин.51.483. Тригонометрия в геометрии
Решающую роль в решении задач на тригонометрию играет знание определений тригонометрических функций.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ:
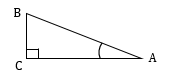
Рассмотрим прямоугольный треугольник ABC и угол A в нем.
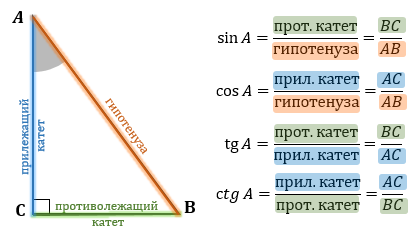
Синус угла — отношение противолежащего катета к гипотенузе.
Косинус угла — отношение прилежащего катета к гипотенузе.
Тангенс угла — отношение противолежащего катета к прилежащему.
Котангенс угла — отношение прилежащего катета к противолежащему.
НАХОЖДЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ:
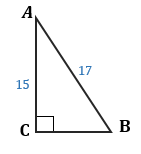
В треугольнике ABC c углом С, равным 90°, гипотенуза AB = 17, а катет AC = 15.
Найдем синус угла B.
$\sin B = \displaystyle\frac<прот.кат.><гип.>=\displaystyle\frac
Чтобы найти косинус угла B, необходимо значение прилежащего катета — BC, которое нам пока неизвестно. Из Пифагоровой тройки 8 : 15 : 17 находим BC = 8.
$\cos B = \displaystyle\frac<прил.кат.><гип.>=\displaystyle\frac
Найдем тангенс угла B.
Найдем котангенс угла B.
Найдем синус угла A.
$\sin A = \displaystyle\frac<прот.кат.><гип.>=\displaystyle\frac
$\cos B = \frac<8><17>\ \,и\ \sin A = \frac<8><17>,\ то\ есть \cos B = \sin A$.
Аналогично можно сказать, что
Можно запомнить эту закономерность. Это происходит, потому что ∠A + ∠B = 90°, и тут вступают в силу формулы приведения, которые более подробно будут в дальнейшем разобраны на курсе.
ТРИГОНОМЕТРИЧЕСКИЕ ФУКНЦИИ — БЕЗРАЗМЕРНЫЕ ВЕЛИЧНЫ:
Важно понимать, что тригонометрические функции — это безразмерные величины (не имеют единиц измерения), они показывают только отношение.
Решение:
Решение:
Ответ: √3
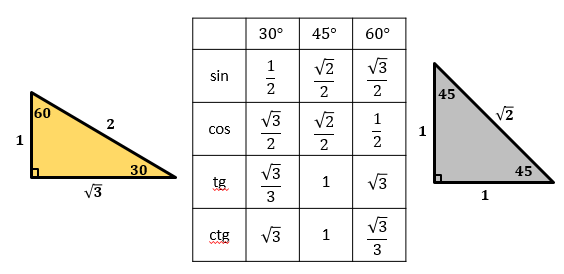
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ:
Таблица основных значений тригонометрических функций предлагает значения sin, cos, tg и ctg от нескольких углов: 0°, 30°, 45°, 60°, 90°.
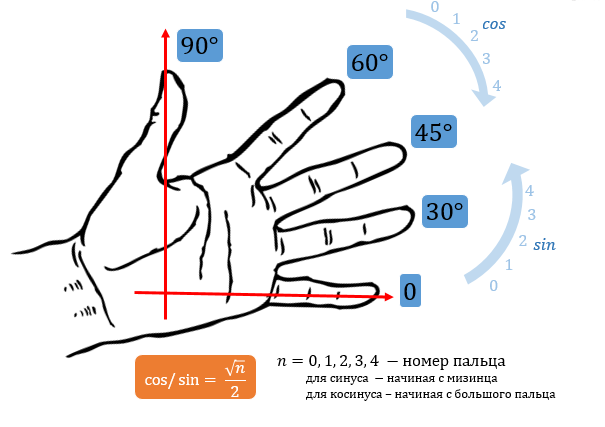
Есть несколько способов нахождения значений тригонометрических функций от табличных углов:
ФОРМУЛЫ, СВЯЗАННЫЕ С ТРИГОНОМЕТРИЧЕСКИМИ ФУКНЦИЯМИ:
1. Основное тригонометрическое тождество:
Основное тригонометрическое тождество — это следствие из теоремы Пифагора для тригонометрического круга. Вот еще один пример получения этой формулы:
Рассмотрим треугольник ABC. Запишем теорему Пифагора для него:
Первое и второе слагаемые — это квадраты синуса и косинуса для угла A или B.
Из основного тригонометрического тождества при наличии значения одной из функций — sin или cos — можно найти вторую.
2. Формулы для тангенса и котангенса.
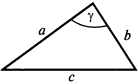
3. Теорема косинусов.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
4. Теорема синусов.
Отношения сторон треугольника к синусам противоположных им углов равны. Это отношение равно 2R, где R — радиус описанной окружности.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Тригонометрия и геометрия в чем разница
Тригонометрия
Тригонометрия в жизни
ТРИГОНОМЕТРИЯ В НАШЕЙ ЖИЗНИ
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
Несколько десятилетий спустя Клавдий Птоломей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу.
· точного определения времени суток;
· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны ;
· нахождения географических координат текущего места;
· вычисления расстояния между городами с известными географическими координатами.
Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест),
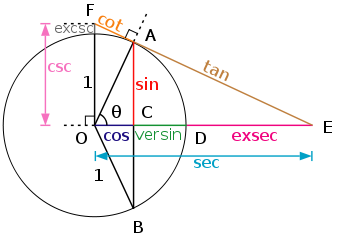
Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось
Модель боритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии. Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея «измерения углов» не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму
d B и измерим длину с отрезка АВ. Затем измерим, например
с помощью астролябии, углы A и B . Эти данные, т.е. c , a и b
позволяют решить треугольник АВС и найти искомое
Затем с помощью теоремы синусов находим d .