Триада и тетрада что это
Использование таблицы треад и тетрад
Таблицу триад и тетрад вы можете увидеть, щелкнув по кнопке в правом нижнем углу сайта. Она нужна для быстрого перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную и наоборот.
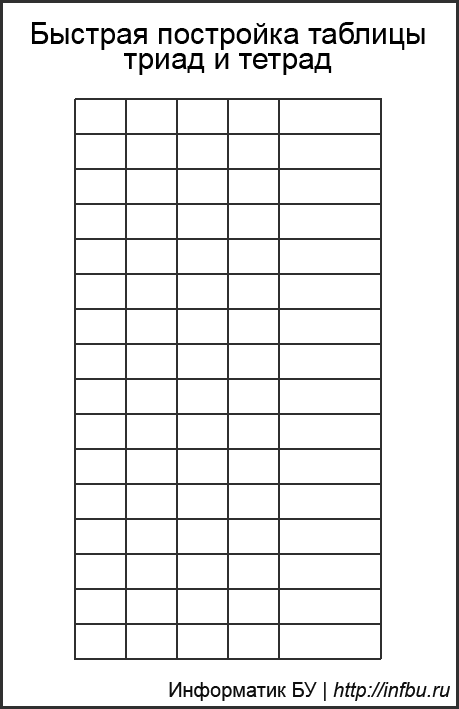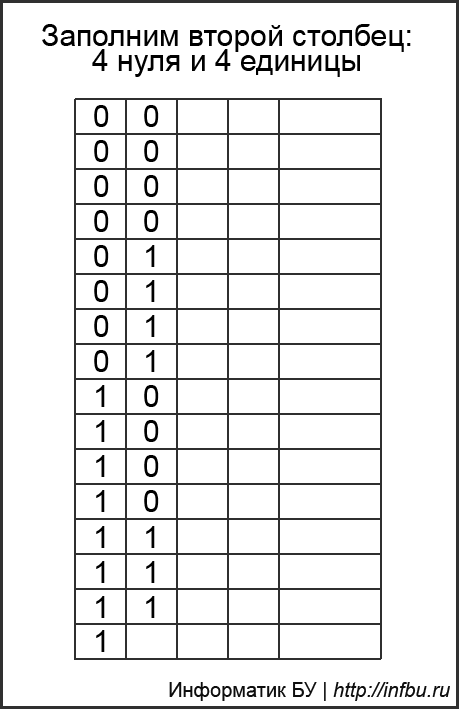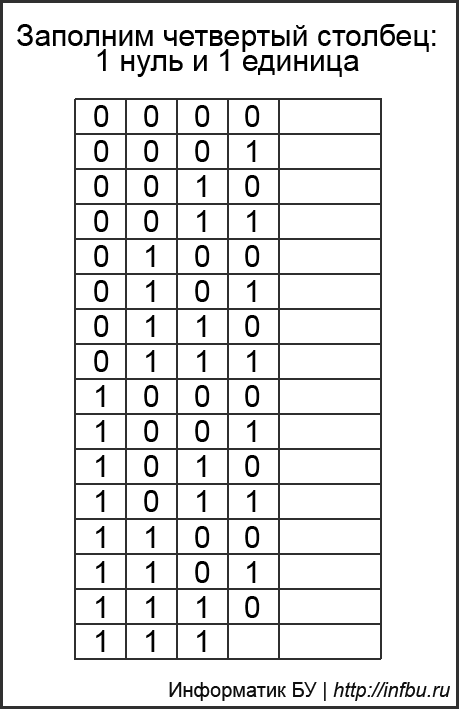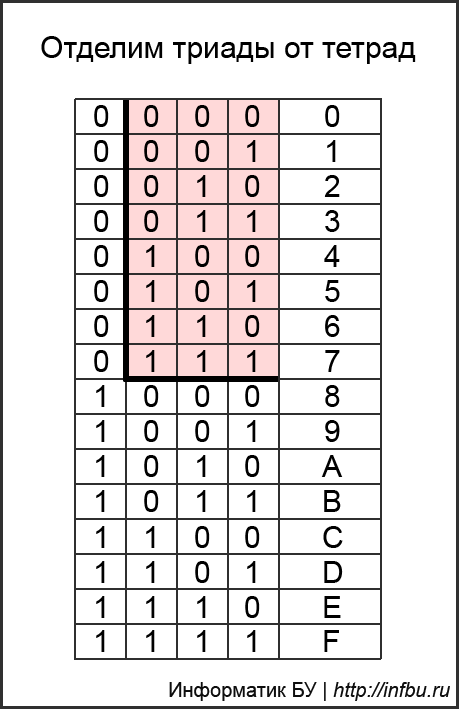
Многие зазубривают таблицу, но она строится очень просто без зубрёжки:
Перевод чисел из восьмеричной системы счисления в двоичную
Возьмем восьмеричное число 34568
Представим каждый разряд числа в виде триады:
Избавимся от первого незначащего нуля и получим результат:
Перевод чисел из двоичной системы счисления в восьмеричную
Возьмем число 111011012
Разделим его на триады, начиная с правого разряда:
Добавим один незначащий нуль:
Заменим триады значениями из таблицы:
Получается, что 3558 = 111011012
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Возьмем число 15F16
Представим каждый разряд в виде тетрады:
Избавимся от трех первых незначащих нулей и запишем результат:
Получается, что 1010111112 = 15F16
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Возьмем число 100010110111012
Разделим его на тетрады, начиная с правого разряда:
0010 0010 1101 1101
Заменим тетрады значениями из таблицы:
Получается, что 22DD16 = 100010110111012
Перевод из одной системы счисления в другую с помощью триад и тетрад
Развивающая – развивать познавательный интерес учащихся, умения применять полученные знания на практике.
Воспитательная – повысить уровень информационной культуры учащихся.
I. Проверка домашнего задания
Вызывается ученик к доске для выполнения домашнего упражнения
II. Изучение нового материала
Так как основания 8-1 и 16-й СС являются степенями двойки, то перевод чисел из этих СС в 2-ую и наоборот прост и основан на методах триад и тетрад. Число делится на триады (тетрады) вправо и влево от десятичной точки. Если крайние триады (тетрады) оказались неполными, они дополняются нулями.
| Алфавит | Триады | Тетрады |
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| А(10) | 1010 | |
| В(11) | 1011 | |
| С(12) | 1100 | |
| D(13) | 1101 | |
| E(14) | 1110 | |
| F(15) | 1111 |
Упражнение: Выполнить перевод, используя тетрады и триады:
IV. Самостоятельная работа
Выполнить перевод, используя тетрады и триады:
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
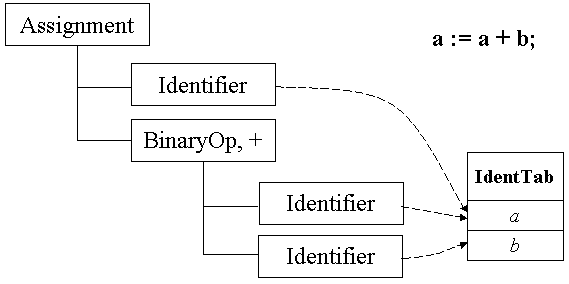
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.
Семантический анализ. Внутреннее представление
Атрибутное дерево разбора
Атрибутное дерево разбора является, наверное, самой распространенной формой организации внутреннего представления программы. При таком подходе каждая исходная конструкция языка представляется в виде узла дерева, содержащего ссылки на все возможные элементы этой конструкции (естественно, каждый отдельный элемент тоже может иметь сложную структуру и, таким образом, также может быть поддеревом). Кроме того, каждый узел дерева может нагружаться дополнительными атрибутами, такими, как ссылки в таблицы представлений или таблицы идентификаторов. В итоге, вся программа представляется в виде единого дерева разбора.
На слайде в качестве примера приведено атрибутное дерево разбора, порожденное по следующему оператору исходного языка a := a + b; Отметим, что форма представления дерева, использованная на слайде, является типичной при компиляции, так как позволяет изобразить практически сколь угодно сложные деревья на экране компьютера (попробуйте представить себе традиционное изображение дерева разбора для сколько-нибудь сложной программы!).
Польская запись
Триады и тетрады
Триады и тетрады представляют собой низкоуровневые формализмы записи промежуточного представления программы, приближающие программу к объектному коду. В этих формализмах все операции записываются в виде последовательности действий, выдающих результаты.
Естественно, триады и тетрады также могут быть расширены для записи всех операций, поддерживаемых на данной целевой платформе.