Три различные плоскости имеют общую точку верно ли что
Аксиомы стереометрии
Содержимое разработки
Школьный курс геометрии состоит из планиметрии и стереометрии.
Планиметрия изучает фигуры и их свойства на плоскости.
Стереометрия изучает фигуры и их свойства в пространстве.
Точки обозначаются прописными латинскими буквами A,B,C,D,E,F….
Прямые обозначаются строчными латинскими буквами a,b,c,d,e,f….
Плоскости обозначаются греческими буквами α,β,γ и т.д.
Основные понятия стереометрии — точка, прямая и плоскость.
Ограниченная часть пространства называется геометрическим телом, а множество точек, ограничивающих его от окружающего пространства, называется поверхностью этого тела.
Закончи предложение, вписав пропущенное(ые) слово(а):
Раздел геометрии, в котором изучаются свойства фигур в пространстве – стереометрия
Через любые три точки, которые не лежат на одной прямой, можно провести только одну плоскость.
Через три точки, лежащие на одной прямой, можно провести бесконечное множество плоскостей.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат плоскости
Через прямую и не лежащую на ней точку можно провести плоскость, притом только одну.
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
Примеры плоскости в природе:
Точки A, B, M, D не лежат в одной плоскости. Верно ли, что плоскости, проходящие через точки A, B, M и через точки B, D, A, пересекаются по прямой AB? Да или нет (подчеркнуть)
Что устойчивее: табуретка на трёх ножках или стул на четырёх ножках? Табуретка
Сколько прямых, которые не пересекают плоскость α, можно провести в пространстве через точку O, если известно, что O∉α? Бесконечное множество.
Могут ли только 3 вершины A, B, C параллелограмма ABCD находиться в одной плоскости? Нет
Верно ли, что через 3 точки, которые находятся на одной прямой, проходит плоскость, и только одна? Нет
Четыре точки A, D, B, C не находятся в одной плоскости. Верно ли, что любые три точки из данных четырёх находятся на одной прямой? Нет
Могут ли две различные плоскости иметь только одну общую точку? Нет
Д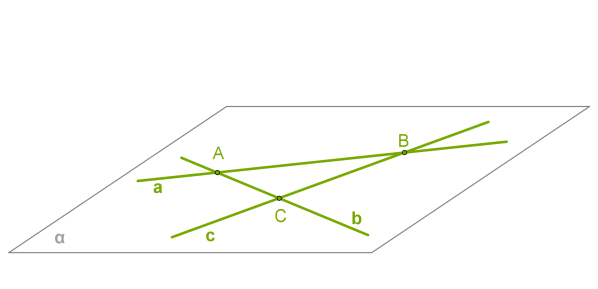 
ве плоскости α и β пересекаются по прямой m. Прямая a находится в плоскости α, а прямая b находится в плоскости β. Прямые b и a пересекаются в точке A. Точка A принадлежит прямой m? Да
Даны 2 различные прямые b и c, которые пересекаются в точке C. Возможно ли, что все прямые, пересекающие данные две прямые и не проходящие через точку C, не находятся в одной плоскости? Нет
Могут ли только 3 вершины A, B, C четырёхугольника ABCD находиться в одной плоскости? Нет
Верно ли, что через 3 точки, которые находятся на одной прямой, проходит плоскость, и только одна? Нет
Четыре точки A, D, B, C не находятся в одной плоскости. Верно ли, что любые три точки из данных четырёх находятся на одной прямой? Нет
Верно ли, что две различные плоскости имеют только две общие точки? Нет
О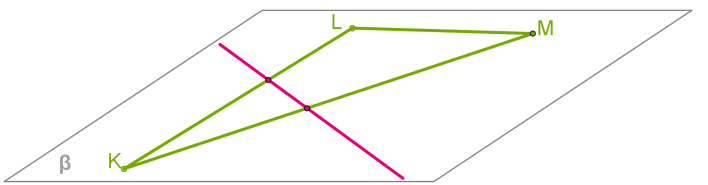 
бязательно ли, что прямая b лежит в плоскости данного треугольника KLM, если она:
пересекает две стороны треугольника? да
проходит через одну из вершин треугольника? Нет
В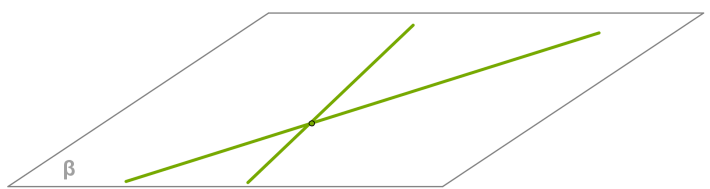 
плоскости β находятся две различные прямые m и n. Будет ли прямая, пересекающая эти прямые m и n, находиться в плоскости β, если прямые m и n пересекаются? Нет
Геометрия. 10 класс
Введение в стереометрию
Введение в стереометрию
Необходимо запомнить
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.
Аксиома 1: Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Теорема 2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.
Введение в стереометрию
Аксиоматический метод – способ построения научной теории, при котором в основу теории кладутся некоторые исходные положения, называемые аксиомами теории, а все остальные предложения теории получаются как логические следствия аксиом.
Определение из математической энциклопедии.
Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них.
Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие.
Определение (дефиниция) – установление смысла незнакомого термина с помощью терминов знакомых и уже осмысленных или путём включения в контекст знакомых слов (контекстуальное определение), или явного формулирования равенства, в левую часть которого входит определяемый термин, а в правую – определяющее выражение, содержащее только знакомые термины.
Теорема (греч. theorema, от theoreo – рассматриваю), в математике – предложение (утверждение), устанавливаемое при помощи доказательства (в противоположность аксиоме). Теорема обычно состоит из условия и заключения. Например, в теореме: если в треугольнике один из углов прямой, то два других – острые, после слова «если» стоит условие, а после «то» – заключение.
Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недоказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами.
Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения. Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём.
«Начала» начинаются с изложения 23 определений и 10 аксиом. Первые пять аксиом – «общие понятия», остальные называются «постулатами».
Пять «общих понятий» Евклида являются принципами измерения длин, углов, площадей, объёмов: «равные одному и тому же равны между собой», «если к равным прибавить равные, суммы равны между собой», «если от равных отнять равные, остатки равны между собой», «совмещающиеся друг с другом равны между собой», «целое больше части».
Первые два постулата определяют действия с помощью идеальной линейки, третий – с помощью идеального циркуля. Четвёртый, «все прямые углы равны между собой», является излишним, так как его можно вывести из остальных аксиом. Последний, пятый постулат гласил: «Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то, при неограниченном продолжении этих двух прямых, они пересекутся с той стороны, где углы меньше двух прямых».
В начале XIX века H. И. Лобачевским и Я. Больяй (J. Bolyai) была открыта, так называемая, неевклидова геометрия, что явилось толчком к дальнейшему развитию аксиоматического метода. Они установили, что, заменив привычный и, казалось бы, единственно «объективно истинный» 5 постулат Евклида о параллельных его отрицанием, можно развивать чисто логическим путем геометрическую теорию, столь же стройную и богатую содержанием, как и геометрия Евклида. Этот факт заставил математиков XIX века обратить внимание на дедуктивный способ построения математической теорий, что повлекло за собой возникновение новой проблематики, связанной с самим понятием аксиоматического метода, и формальной (аксиоматической) математической теории.
Три различные плоскости имеют общую точку верно ли что
одну или бесконечно много
одну или бесконечно много
П – 2. Параллельные прямые в пространстве. Параллельность прямой и плоскости.
Вариант А1
Вариант А2
Верно ли, что две параллельные прямые лежат в одной плоскости?
Верно ли, что две прямые, лежащие в одной плоскости, параллельны?
Может ли прямая, параллельная плос-кости, пересекать какую-либо прямую этой плоско-сти?
Может ли прямая, пересекающая плоскость, быть параллельна какой-либо прямой этой плоскости?
Поставьте вместо пропуска слова «прямой» или «плоскости» так, чтобы данное утверждение было верным:
Поставьте вместо пропуска слова «прямой» или «плоскости» так, чтобы данное утверждение было верным:
П – 2. Параллельные прямые в пространстве. Параллельность прямой и плоскости.
Вариант Б1
Вариант Б2
Верно ли, что если одна из двух параллельных прямых лежит в некоторой плоско-сти, то и вторая прямая лежит в этой плоскости?
Верно ли, что если одна из двух
параллельных прямых пересекает некоторую плоскость, то и вторая прямая пересекает эту плоскость?
Может ли прямая в пространстве пе-ресекать одну из двух па-раллельных прямых, но не пересекать другую?
Может ли плоскость быть параллельной одной из двух параллельных прямых и не быть параллельной другой прямой?
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным:
каждой из двух дан-ных прямых, то данные прямые могут пересекаться».
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным:
П – 2. Параллельные прямые в пространстве. Параллельность прямой и плоскости.
Вариант В1
Вариант В2
Верно ли, что две прямые, параллельные одной плоскости, параллельны?
Верно ли, что плоскость, параллельная одной из двух параллельных прямых, параллельна и второй прямой?
Могут ли прямые АВ и CD быть параллельными, если прямые AD и ВС пересекаются?
Могут ли прямые АВ и CD быть параллельными, если точка D не лежит в плоскости АВС?
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным:
Поставьте вместо пропуска слова «прямая» или «плоскость» так, чтобы данное утверждение было верным:
П – 2. Параллельные прямые в пространстве. Параллельность прямой и плоскости.
Вопросы по стереометрии.
3. Могут ли две различные плоскости иметь только две общие точки?
а) Никогда;
б) могу, но при дополнительных условиях;
в) всегда имеют;
г) нельзя ответить на вопрос;
д) другой ответ.
4. Точки K, L, M лежат на одной прямой, точка N не лежит на ней. Через каждые три точки проведена одна плоскость. Сколько различных плоскостей при этом получилось?
а) 1; б) 2; в) 3; г) 4; д) бесконечно много.
5. Выберите верное утверждение.
а) Через любые три точки проходит плоскость, и притом только одна;
б) если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости;
в) если две плоскости имеют общую точку, то они не пересекаются;
г) через прямую и точку, лежащую на ней, проходит плоскость, и притом только одна;
д) через две пересекающиеся прямые плоскость провести нельзя.
6. Назовите общую прямую плоскостей PBM и MAB.
а) PM; б) AB; в) PB; г) BM; д) определить нельзя.
8.Две плоскости пересекаются по прямой с. Точка М лежит только в одной из плоскостей. Что можно сказать о взаимном положении точки М и прямой с?
а) Никакого вывода сделать нельзя;
б) прямая с проходит через точку М;
в) точка М лежит на прямой с;
г) прямая с не проходит через точку М;
д) другой ответ.
9. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном положении прямых а, b и c?
а) Все прямые лежат в разных плоскостях;
б) прямые а и b лежат в одной плоскости;
в) все прямые лежат в одной плоскости;
г) ничего сказать нельзя;
д) прямая с совпадает с одной из прямых: или с а, или с b.
10. Прямые а и b пересекаются в точке О. A € a, B € b, Y € AB. Выберите верное утверждение.
а) Точки O и Y не лежат в одной плоскости;
б) прямые OY и a параллельны;
в) прямые a, b и точка Y лежат в одной плоскости;
г) точки O и Y совпадают; д) точки Y и A совпадают.