Треугольник в формуле это что
Как найти площадь треугольника
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
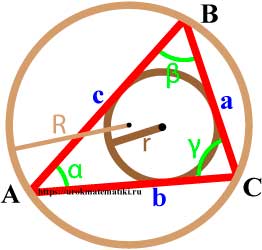
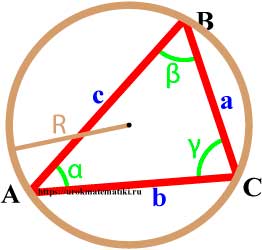
3. Площадь треугольника через описанную окружность и стороны
4. Площадь треугольника через вписанную окружность и стороны
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
Площадь прямоугольного треугольника по формуле Герона
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Треугольник
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
Остроугольный треугольник
— все углы треугольника острые.
Тупоугольный треугольник
— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник
— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник
Равносторонний (правильный) треугольник
— все три стороны равны.
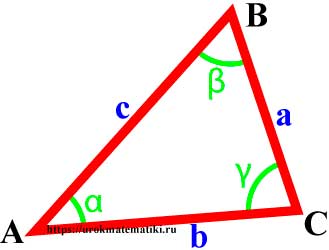
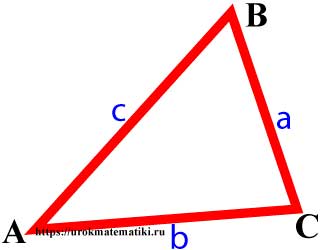
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
a sin α = b sin β = c sin γ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
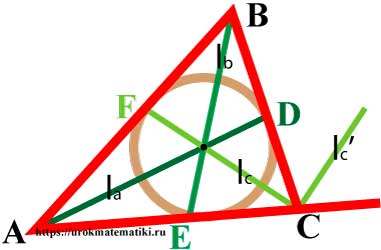
Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника
S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника
Угол между l c и l c ‘ = 90°
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
где p = a + b + c 2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
l a = 2 b c cos α 2 b + c
l b = 2 a c cos β 2 a + c
l c = 2 a b cos γ 2 a + b
Высоты треугольника
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
Свойства высот треугольника
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
h a = b sin γ = c sin β
h b = c sin α = a sin γ
h c = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
Радиус вписанной в треугольник окружности через три стороны
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
Радиус описанной окружности через площадь и три угла
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
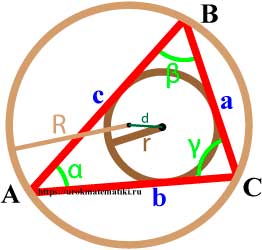
Связь между вписанной и описанной окружностями треугольника
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
Радиус описанной окружности через площадь и три угла
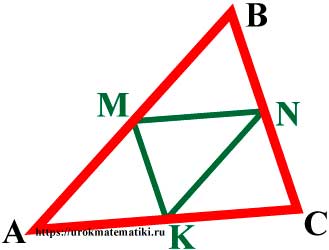
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон.
Формулы площади треугольника
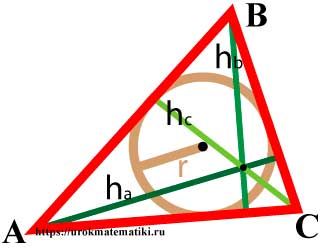
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
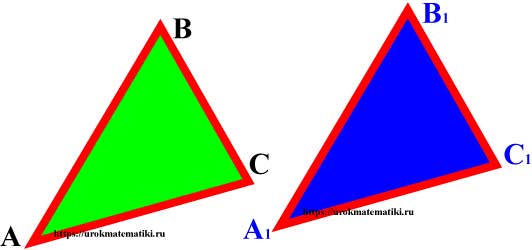
Равенство треугольников
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
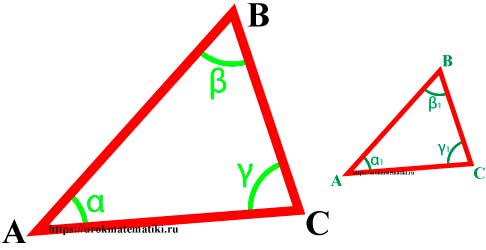
Подобие треугольников
Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
где k — коэффициент подобия.
Признаки подобия треугольников
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∡A — прямой, ∡B = 30°, и значит, что ∡C = 60°.
Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
Формулы длины стороны (основания), (b ):
4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Геометрия. Урок 3. Треугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение треугольника
Треугольник – многоугольник с тремя сторонами и тремя углами.
Виды треугольников

Основные свойства треугольника:
Отрезки в треугольнике
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
Площадь треугольника
Площадь произвольного треугольника можно найти следующими способами:
Равнобедренный треугольник
Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.

Свойства равноберенного треугольника:
Равносторонний треугольник
Равносторонним называется треугольник, у которого все стороны и все углы равны.
Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Прямоугольный треугольник
Свойства прямоугольного треугольника:
Теорема Пифагора
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с треугольниками
Геометрическая фигура: треугольник
В данной публикации мы рассмотрим определение, классификацию и свойства одной из основных геометрических фигур – треугольника. Также разберем примеры решения задач для закрепления представленного материала.
Определение треугольника
Треугольник – это геометрическая фигура на плоскости, состоящая из трех сторон, которые образованы путем соединения трех точек, не лежащих на одной прямой. Для обозначения используется специальный символ – △.
Углы можно, также, обозначать с помощью специального знака “∠“:
Классификация треугольников
В зависимости от величины углов или количества равных сторон выделяют следующие виды фигуры:
1. Остроугольный – треугольник, у которого все три угла острые, т.е. меньше 90°.
2. Тупоугольный – треугольник, в котором один из углов больше 90°. Два остальных угла – острые.
3. Прямоугольный – треугольник, в котором один из углов является прямым, т.е. равен 90°. В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).
4. Разносторонний – треугольник, у которого все стороны имеют разную длину.
5. Равнобедренный – треугольник, имеющие две равные стороны, которые называются боковыми (AB и BC). Третья сторона – это основание (AC). В данной фигуре углы при основании равны (∠BAC = ∠BCA).
6. Равносторонний (или правильный) – треугольник, у которого все стороны имеют одинаковую длину. Также все его углы равны 60°.
Свойства треугольника
1. Любая из сторон треугольника меньше двух оставшихся, но больше их разности. Для удобства примем стандартные обозначения сторон – a, b и с. Тогда:
Это свойство применяется для проверки отрезков на предмет того, могут ли они образовывать треугольник.
2. Сумма углов любого треугольника равняется 180°. Из этого свойства следует, что в тупоугольном треугольнике два угла всегда являются острыми.
3. В любом треугольнике напротив большей стороны находится больший угол, и наоборот.
Примеры задач
Задание 1
В треугольнике известны два угла – 32° и 56°. Найдите значение третьего угла.
Задание 2
Даны три отрезка длиной 4, 8 и 11. Выясните, могут ли они образовать треугольник.
Решение
Составим неравенства для каждого из заданных отрезков, исходя из свойства, рассмотренного выше:
11 – 4