Трехмерное пространство что это простыми словами
Трёхмерное пространство
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.
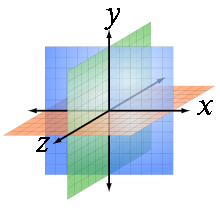
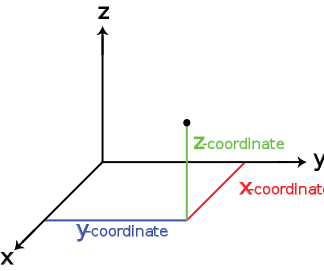
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением иногда называют время).
Трёхмерное пространство
Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется глубиной восприятия.
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением континуума, как правило, называют время — неоднородное качество по отношению к пространственной мерности). [3]
Многомерные пространства — 3D, 4D и другие измерения
Илья Щуров, Jason Hise, ashgrowen, Анатолий Белов
Многомерные пространства
Что такое четырёхмерное пространство («4D»)?
Представление других измерений
Что такое гиперкуб? Построение тессеракта
Виды гиперкубов и их названия
Как насчет 10D?
Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?
Мы достаточно часто слышим что-нибудь вроде «трехмерное пространство», или «многомерное пространство», или «четырехмерное пространство». Возможно, вы знаете, что мы живем в четырехмерном пространстве-времени. Что это означает и почему это интересно, почему математики и не только математики изучают такие пространства?
Об авторах
Илья Щуров — кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ.
Jason Hise — Physics programmer at Ready at Dawn Studios, 4D geometry enthusiast. Автор анимированных моделей, представленных в данной статье.
ashgrowen — пикабушник, проиллюстрировавший в этой статье построение тессеракта и гиперкуба.
Давайте начнем с простого — начнем с одномерного пространства. Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.
Например, если мы говорим про города, то можно перейти от одномерного пространства к двумерному. Примером двумерного пространства является плоскость, а если мы продолжим нашу аналогию с городами, то это город, в котором можно расчертить улицы, допустим, перпендикулярно друг другу, как это сделано в Нью-Йорке, в центре Нью-Йорка. Там есть «стрит» и авеню, каждая из которых имеет свой номер, и вы можете задавать местоположение на плоскости, задавать два числа. Опять же, все мы знаем декартову систему координат, знакомую со школы, — каждая точка задается двумя числами. Это пример двумерного пространства.
Но если мы говорим про город типа центра Нью-Йорка, то на самом деле он является трехмерным пространством, потому что вам мало задать, например, конкретный дом, пусть даже вы зададите его пересечением какой-нибудь «стрит» и какой-нибудь авеню, — вам нужно будет задать еще и этаж, на котором находится нужная вам квартира. Это даст вам третье измерение — высоту. У вас получится трехмерное пространство, в котором каждая точка задается тремя числами.
Вопрос: что такое четырехмерное пространство? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.
Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.
Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.
В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.
Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.
Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.
Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.
У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.
Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид, разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.
Что такое четырёхмерное пространство («4D»)?
Тессерракт — четырехмерный куб
Всем знакомо сокращение 3D, означающее «трёхмерный» (буква D — от слова dimension — измерение). Например, выбирая в кинотеатре фильм с пометкой 3D, мы точно знаем: для просмотра придётся надеть специальные очки, но зато картинка будет не плоской, а объёмной. А что такое 4D? Существует ли «четырёхмерное пространство» в реальности? И можно ли выйти в «четвёртое измерение»?
Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.
Сдвинем теперь точку по прямой на некоторое расстояние. Допустим, что наша точка — остриё карандаша; когда мы её сдвинули, она прочертила отрезок. У отрезка есть длина, и больше никаких измерений: он одномерен. Отрезок «живёт» на прямой; прямая является одномерным пространством.
Тессеракт — четырехмерный куб
Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).
Если сдвинуть прямоугольник в направлении, перпендикулярном плоскости, в которой он лежит, получится «кирпичик» (прямоугольный параллелепипед) — трёхмерный объект, у которого есть длина, ширина и высота; он расположен в трёхмерном пространстве, в таком, в каком живём мы с вами. Поэтому мы хорошо представляем себе, как выглядят трёхмерные объекты. Но если бы мы жили в двумерном пространстве — на плоскости, — нам пришлось бы изрядно напрячь воображение, чтобы представить себе, как можно сдвинуть прямоугольник, чтобы он вышел из той плоскости, в которой мы живём.
Тессеракт — четырехмерный куб
Представить себе четырёхмерное пространство для нас также довольно непросто, хотя очень легко описать математически. Трёхмерное пространство — это пространство, в котором положение точки задаётся тремя числами (например, положение самолёта задаётся долготой, широтой и высотой над уровнем моря). В четырёхмерном же пространстве точке соответствует четвёрка чисел-координат. «Четырёхмерный кирпич» получается сдвигом обычного кирпичика вдоль какого-то направления, не лежащего в нашем трёхмерном пространстве; он имеет четыре измерения.
На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.
Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.
Представление других измерений
От 2D к 3D
Ранняя попытка объяснить концепцию дополнительных измерений появилась в 1884 году с публикацией романа о плоской земле Эдвина А. Эббота «Флатландия: романтика множества измерений«. Действие в романе разворачивается в плоском мире, называемом «Флатландия», а повествование ведется от лица жителя этого мира — квадрата. Однажды во сне квадрат оказывается в одномерном мире — Лайнландии, жители которой (треугольники и другие двумерные объекты представлены в виде линий) и пытается объяснить правителю этого мира существование 2-го измерения, однако, приходит к выводу о том, что его невозможно заставить выйти за рамки мышления и представления только прямых линий.
Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.
Сфера, с точки зрения Квадрата — Окружность. │ commons.wikimedia.org
Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.
Сфера пытается объяснить квадрату устройство трехмерного мира, но квадрат понимает только понятия «вверх/вниз» и «лево/право», он не способен постичь понятия «вперед/назад».
Непостижимая Квадратом тайна третьего измерения на примере прохождения сферы через плоскость. Герой наблюдает уменьшение Окружности до точки и её исчезновение. │ commons.wikimedia.org
Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.
Квадрат, вооруженный своим новым знанием, начинает осознавать возможность существования четвертого измерения. Также он приходит к мысли, что число пространственных измерений не может быть ограничено. Стремясь убедить сферу в этой возможности, квадрат использует ту же логику, что и сфера, аргументирующая существование трех измерений. Но теперь из них двоих становится «близорукой» сфера, которая не может понять этого и не принимает аргументы и доводы квадрата — так же, как большинство из нас «сфер» сегодня не принимают идею дополнительных измерений.
От 3D к 4D
Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.
Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..
Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.
Что такое гиперкуб? Построение тессеракта
Виды гиперкубов и их названия
1. Точка — нулевое измерение
2. Отрезок — одномерное пространство
3. Квадрат — двумерное пространство (2D)
4. Куб — трёхмерное пространство (3D)
5. Тессеракт — четырёхмерное пространство (4D)
6. Пентеракт — пятимерное пространство (5D)
7. Хексеракт — шестимерное пространство (6D)
8. Хептеракт — семимерное пространство (7D)
9. Октеракт — восьмимерное пространство (8D)
10. Энтенеракт — девятимерное пространство (9D)
11. Декеракт — десятимерное пространство (10D)
Гиперкуб — это обобщающее название куба в производном числе измерений. Всего измерений десять, плюс точка (нулевое измерение).
Соответственно, существует одиннадцать видов гиперкуба. Рассмотрим построение тессеракта — гиперкуба четвертого измерения:
Для начала построим точку А (рис. 1):
После, соединим ее с точкой В. Получим вектор АВ (рис. 2):
Построим вектор, параллельный вектору АВ, и назовем его CD. Соединив начала и концы векторов, получим квадрат ABDC (рис. 3):
Теперь построим еще один квадрат A1B1D1C1, который лежит в параллельной плоскости. Соединив точки подобным образом, получим куб (рис. 4):
У нас есть куб. Представьте, что положение куба в трехмерном пространстве с течением времени изменилось. Зафиксируем его новое местоположение (рис 5.):
Рис. 5 Измененное положение куба в пространстве
А теперь, мы проводим вектора, которые соединяют местоположение точек в прошлом и в настоящем. Получаем тессеракт (рис. 6):
Рис. 6 Тессеракт (построение)
Подобным образом строятся остальные гиперкубы, конечно же учитывается смысл пространства, в котором гиперкуб находится.
Как насчет 10D?
В 1919 году польский математик Теодор Калуца предположил, что существование четвертого пространственного измерения может увязать между собой общую теорию относительности и электромагнитную теорию. Идея, впоследствии усовершенствованная шведским математиком Оскаром Кляйном, заключалась в том, что пространство состояло как из «расширенных» измерений, так и из «свернутых» измерений. Расширенные измерения — это три пространственных измерения, с которыми мы знакомы, и свернутое измерение находится глубоко в расширенных размерах. Эксперименты позже показали, что свернутое измерение Калуцы и Кляйна не объединило общую теорию относительности и электромагнитную теорию, как это первоначально предполагалось, но спустя десятилетия теоретики теории струн нашли эту идею полезной, даже необходимой.
Математика, используемая в теории суперструн, требует не менее 10 измерений. То есть для уравнений, описывающих теорию суперструн и для того чтобы связать общую теорию относительности с квантовой механикой, для объяснения природы частиц, для объединения сил и т. д. — необходимо использовать дополнительные измерения. Эти измерения, по мнению теоретиков струн, завернуты в свернутое пространство, изначально описанное Калуцей и Кляйном.
Круги представляют собой дополнительный пространственный размер, свернутый в каждую точку нашего знакомого трехмерного пространства. │ WGBH / NOVA
Чтобы расширить скрученное пространство, чтобы включить эти добавленные размеры, представьте, что круги Калуцы-Клейна заменяются сферами. Вместо одного добавленного измерения мы имеем два, если рассматривать только поверхности сфер и три, если учесть пространство внутри сферы. Получилось всего шесть измерений. Так где же другие, которые требует теория суперструн?
Оказывается, что до того, как появилась теория суперструн, два математика Эудженио Калаби из Университета Пенсильвании и Шин-Тунг Яу из Гарвардского университета описали шестимерные геометрические формы. Если мы заменим сферы в скрученном пространстве этими формами Калаби-Яу, мы получим 10 измерений: три пространственных, а также шестимерные фигуры Калаби-Яу.
Шестимерные формы Калаби-Яу могут объяснять дополнительные размеры, требуемые теорией суперструн. │ WGBH / NOVА
Приверженцы теории струн делают ставку на то, что дополнительные измерения действительно существуют. На самом деле, уравнения, описывающие теорию суперструн, предполагают вселенную с не менее чем 10 измерениями. Но даже физикам, которые все время думают о дополнительных пространственных измерениях сложно описать как они могут выглядеть, или как люди могли бы приблизиться к их пониманию.
Если теория суперструн будет доказана и идея мира, состоящего из 10 или более измерений, подтвердится, то появится ли когда-нибудь объяснение или визуальное представление более высоких измерений, которые сможет постичь человеческий разум? Ответ на этот вопрос навсегда может стать отрицательным, если только какая-то четырехмерная жизненная форма не «вытащит» нас из нашего трехмерного мира и не даст нам увидеть мир с ее точки зрения.