Трехмерное измерение что это такое
Трёхмерное пространство
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.
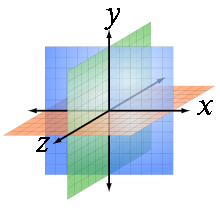
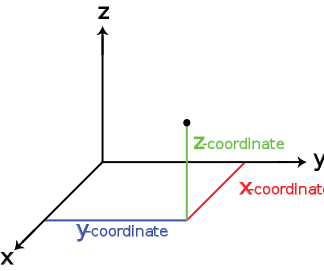
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Также существуют другие системы координат, наиболее часто используются цилиндрическая и сферическая системы.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Трёхмерное пространство имеет несколько свойств, которые отличают его от пространств другой размерности. Например, это пространство наименьшей размерности, в котором можно завязать узел на куске верёвки. Многие законы физики, например многие законы обратных квадратов связаны с тем что размерность нашего пространства три.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением иногда называют время).
Трёхмерное пространство
Трёхме́рное простра́нство — геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — высоту, ширину и длину, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется глубиной восприятия.
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Нульмерное, одномерное и двухмерное пространства могут рассматриваться как располагающиеся в трёхмерном пространстве; само оно может считаться частью модели четырёхмерного пространства (четвёртым измерением континуума, как правило, называют время — неоднородное качество по отношению к пространственной мерности). [3]
Трёхмерное пространство
Из Википедии — свободной энциклопедии
Трёхме́рное простра́нство — геометрическая модель материального мира. Это пространство называется трёхмерным, так как оно имеет три однородных измерения — длину, ширину и высоту, то есть трёхмерное пространство описывается тремя единичными ортогональными векторами.
Понимание трёхмерного пространства людьми, как считается, развивается ещё в младенчестве, и тесно связано с координацией движений человека. Визуальная способность воспринимать окружающий мир органами чувств в трёх измерениях называется восприятием глубины.
В аналитической геометрии каждая точка трёхмерного пространства описывается как набор из трёх величин — координат. Задаются три взаимно перпендикулярных координатных оси, пересекающихся в начале координат. Положение точки задаётся относительно этих трёх осей заданием упорядоченной тройки чисел. Каждое из этих чисел задаёт расстояние от начала отсчёта до точки, измеренное вдоль соответствующей оси, что равно расстоянию от точки до плоскости, образованной другими двумя осями.
Другой взгляд даёт линейная алгебра, где важную роль играет понятие линейной независимости. Пространство трёхмерно по той причине, что высота коробки не зависит от её длины и ширины. На языке линейной алгебры пространство трёхмерно, потому что каждая точка может быть задана комбинацией из трёх линейно независимых векторов. В этих терминах пространство-время четырёхмерно, потому что положение точки во времени не зависит от её положения в пространстве.
Трехмерное измерение что это такое
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Структура мироздания. Описание семи видов измерений нашей Вселенной
Прежде всего хочу выразить свою благодарность Сухоносу Сергею Ивановичу. Без его труда, без его усилия решить проблему множественности измерений нашей Вселенной не было бы и этой работы. Именно он убедил меня изложить свои идеи на бумаге и сделать их достоянием широкой общественности.
И так, как же устроена наша Вселенная?
Уйдём сначала в микромир и закончим формой Вселенной.
Первое измерение по порядковому номеру, но правильнее его называть нулевым измерением, это точка. Точка не имеет оси координат. Имеется ли материальный носитель первого измерения? Прежде всего, хочу отметить, что Вселенною я представляю ни как случайное нагромождение материальных объектов после большого взрыва, а как осознанное творение личности. Кто-то эту личность называет Богом, но правильнее называть его Творцом.
Есть расхожее выражение: движение – это жизнь. Но это не верно. Ведь что такое ветер как ни движение молекул газа в пространстве. Движутся планеты, движутся звёзды. Правильнее такое движение назвать перемещением в пространстве. А вот вибрация совсем другое. Её можно представить, как сжимающийся и расширяющийся шарик. Живатма – это энергетический шарик, являющийся основой всего мироздания.
Таким образом, важно сразу осознать, что у Живатмы изначально не было свободы выбора кем стать в будущем, судьба её была предопределена.
Кроме интереса у Живатмы познать мир, в неё было вложено стремление найти себе подобную. Это стремление в конце концов выливается в образовании новой структуры во Вселенной, нового измерения.
Когда Живатма наконец встречает себе подобную, между ними возникает связь. Две точки соединяются в линию. Эту связь правильно назвать любовью. Ведь что такое любовь, как ни беззаветная привязанность. Смысл этой связи двух энергетических частиц не в желание слиться друг с другом, а в желание любоваться друг другом, быть всегда рядом друг с другом. Примечательно, что, если что-то происходит с одной частицей, вторая тут же об этом узнаёт. Если первое измерение правильнее назвать измерением энергии, то второе измерение – это уже информация. Во втором измерении появляются две новых эмоции – любовь и страх потерять эту любовь.
Какова функция второго измерения? Две точки, соединённые между собой некой линией, можно назвать отрезком. Эти отрезки не просто так разбросаны во Вселенной. Они соединены в некие кластеры, структуру, повторяющую себя при увеличении масштаба. Правильно утверждают некоторые учёные, что наша Вселенная устроена по принципу голограммы. Каждый участок Вселенной есть организационная копия всей Вселенной. Как красиво говорится у некоторых народов, не развращённых современной цивилизацией: «Если где-то срывается травинка – вздрагивает всё мироздание». И так, функция второго измерения – каждый связан с каждым, одно влияет на всё.
Таким образом, мы имеем две сознательные точки, связанные любовь. Эта связь не может быть бесплодной. Рано или поздно она рождает плод, новую точку.
В третьем измерении появляется новое явление – колебание. Представьте равнобедренный треугольник вершиной верх. Так вот, вершина начинает колебаться вверх – вниз, проходя через прямую линию, соединяющую две точки по бокам. Такое явление называется стоячая волна. Появилось пространство. Но если вершины амплитуд колебания перемещаются в пространстве, то появляется продольная волна, появляется время. Чтобы появилась продольная волна наши треугольники должны соединится в цепочку. Это соединение должно иметь нечто особенное по сравнению с соединениями отдельных Живатм. Его правильнее назвать дружба. Мы научимся управлять временем, когда научимся управлять продольной волной, останавливать её или направлять в другую сторону. В третьем измерении появляются такие чувства как красота и гармония, и их антиподы.
Волна может рождать частицу, но при определённых условиях. Учёные уже обнаружили, что если за электромагнитной волной начинают наблюдать, то она тут же меняет свои свойства и начинает себя вести не как волна, а как пучок элементарных частиц. И этот пучок ведёт себя уже по совершенно другим закона. То есть, если за нашей троицей кто-то начинает наблюдать, в нашем случае это может быть только Творец, то троица сразу же объединяется в единство, в элементарную частицу. Она из непроявленного состояния электромагнитной волны переходит в проявленное и ведет себя как единое целое. В этом заключается её триединство.
Не забываем, что в каждую частицу мироздания вложено желание вернуться к Создателю. Через некоторое время три наших точки пространства начинают страстно желать быть наблюдаемым Творцом не периодически, а постоянно. Создатель откликается на это желание и посылает троице четвёртую точку, дух божий, который уже на постоянной основе будет связан с ней. С этого момента появляется вещество, так называемый материальный мир.
И так, треугольник в основании и вершиной над ним образуют объёмную фигуру – трёхгранную пирамиду. Появляется трёхмерное измерение с тремя осями координат. Это мир, в котором мы живём. Некоторые ученые наш мир справедливо приписывают к четвёртому измерению, добавляя к трём осям координат время. Но это не верно.
Что же принципиально нового произошло в четвёртом измерении? Время и пространство уже были и до этого. Теперь, как это ни странно прозвучит, в каждом атоме, в каждой молекуле, в каждом камне не зримо присутствует Господь. Он наблюдает, что же происходит с нашей троицей. Мир вещества эволюционирует и меняется. Атомы соединяются в молекулы, образуя четыре разновидности агрегатного состояния: газ, жидкость, минералы и плазма. В науке соединение атомов друг с другом называется валентностью. Мы же, по аналогии с другими типами соединений, назовём его симпатией. Могу предположить, что в плазме мы имеем дело с активной антипатией. Эволюция продолжается и появляются живые объекты. Живое от неживого отличается наличием обмена веществ, репродуктивной функцией и сексуальным влечением. Венцом эволюции живого является человек разумный.
Есть ещё очень важное новое, что появляется в четвёртом измерении – это личная история или индивидуальная душа. Дело в том, что любовь всегда животворит, она всегда приносит плод. Любовь двух Живатм родила новую Живатму подобной первым двум. В нашей схеме четвёртого измерения – трёхгранной пирамиде присутствует уже четыре объекта: три Живатмы и Дух Творца. Они тоже связанны любовью и эта любовь обязательно должна дать плод, новое дитя, новую сущность мироздания, но уже отличную от четырёх. Эта сущность называется индивидуальная душа. И вот мы переходим к пятому измерению.
Где же появляется новая точка в нашей схеме трёхгранной пирамиды. Она помещается в центр её. В трёхмерном мире появляется новая ось координат, направленная внутрь. В природе появилась новая сущность – душа, и под неё создаётся новый мир – духовный мир или загробный мир. У него есть свои специфические задачи и свойства. Загробный мир многопланов и разнообразен. Там обитают не только души людей, но и души животных, растений и минералов.
У сущностей в духовном мире появляются две совершенно новые способности: видеть объекты одновременно снаружи и внутри и способность творить объекты с помощью мысли. Если на Земле практически свойственно обманывать друг друга, то в загробном мире это не получится. Духовная сущность слышит мысли другой сущности и видит её нравственную суть. Также души могут летать и мгновенно перемещаться в пределах разрешённой зоны.
Цель загробной жизни – оценить свою воплощённую жизнь, осознать «ошибки», наметить следующую жизнь для их исправления. Следует также не забывать, духовные сущности могут напрямую вмешиваться в жизнь людей как положительно (ангелы хранители), так и отрицательно (бесы, лярвы и т.п.).
В загробном мире очень трудно отрицать существование Бога, так как любой материалист воочию убеждается, что всё обстоит совсем не так как он думал. Понятно так же, что существуют более продвинутые души и мене. Для разных душ существуют разные Обители, разные Небеса. Некоторые источники утверждают, что Небес семь. Я полагаю их больше.
И вот постепенно особенно развитые души начинают осваивать уникальную даже для духовного мира способность. Я имею ввиду способность одной души находится одновременно сразу в нескольких местах. Затем они приобретают способность воплощаться сразу в нескольких телах. И вот мы подошли к шестому измерению.
Откуда же взялось это движения и почему раньше все фигуры были статичными? Дело в том, что раньше элементы пирамиды соединяла любовь, желание быть рядом. Теперь же центральная точка пирамиды – индивидуальная душа соединяется с вершиной, с духом божьем не просто любовью, хотя и она конечно присутствует, но и стремлением слиться, стать единым целым. Вот это стремление и сообщает фигуре поступательное движение. Вращение же вызвано тем, что нижние вершины пирамиды – отец, мать и дитя не тождественны друг другу, то есть имеют свою индивидуальность, различаются.
Какова же функция мира богов? Появляются две новых функции – творить и править. У древних славян мир четвертого измерения назывался миром яви, пятого измерения – миром нави, а шестого – миром прави.
Там, где в природе мы видим спираль, можно не сомневаться, это дело рук богов. Спираль ДНК образует всё живое, планеты движутся вокруг своих звёзд не по кругу, а по спирали, поскольку сама звезда движется. Но движется она не просто прямо, а по спирали в своей галактике. Точно также и галактики во Вселенной двигаются по спирали.
Следует отметить, что дух Земли, дух луны, дух солнца – это уже боги. Эти боги не просто отслеживают и управляют своими обитателями, но также могу и реинкарнировать в них и уже через телесную форму взаимодействовать со своими жителями. Есть планеты, где обитают сущности четвёртого измерения, есть, где живут души умерших.
Напоминаю, что боги наиболее приблизились к своему Творцу. И тяга слиться с ним у них конечно же не пропала. И этот долгожданный момент обязательно случается. Вот мы и подошли к последнему седьмому измерению.
Седьмое измерение – это Творец нашей Вселенной или просто наша Вселенная, что суть одно и тоже. Каков же графический символ Творца? Всё просто. Боги – спирали, вытягиваясь и собираясь в линию, в конце концов замыкаются в круг сами на себя. Появляется фигура тора. Наша Вселенная имеет фигуру то тора, то шара, сейчас мы к этому подойдём.
И так, что же нового мы имеем на седьмом измерении? Это всеведение, вездесущность и всемогущество. Какая основная эмоция Творца? Это бесстрастность. Какая основная деятельность Творца кроме творения? Это наблюдение. Вы только представьте сущность, которая всё знает и всё может. Это же тоска зелёная! И поэтому Творцу ничего не остаётся, как найти способ забыть, что Он всё может и всё знает. И для этого есть только один разумный способ – временно реинкарнироваться в менее развитое существо и насладиться палитрой новых и сильных эмоций.
Помните, что все сущности стремятся слиться с Творцом. На уровне бога им это удаётся. И вот тут случается чудо. Они и сливаются с Творцом и осознают себя как индивидуальность. Это как бы единство во множественности. У слившейся души появляется две возможности: оставаться с Творцом, есть что посмотреть, есть, что вспомнить. Или выделится и начать создавать свою вселенную, заняться собственным творчеством.
Следует отметить ещё одну интересную особенность Творца, о которой не все знают. Творец то бодрствует, то спит. Когда Он бодрствует, то вселенная имеет форму тора. Когда Он засыпает, то Вселенная начинает сжиматься и в конце концов приобретает форму шара. В этот момент всякая жизнь во Вселенной прекращается.
В индуизме даже известно, как долго Творец спит и бодрствует. Так продолжительность жизни Брахмы (читай период бодрствования) длится 100 лет, а день Брахмы, называемый кальпа равен 4,32 миллиардов лет. Сняться ли Творцу сну? Уверен, что да. Ведь когда-то он был таким же человеком, как и мы с вами. А как известно – что внизу, то и на верху. Таким образом, графически седьмое измерение правильнее изобразить как пульсирующий тор.
Когда Творец просыпается, учёные это называют большим взрывом, начинается процесс нового творения, развёртывание новой Вселенной. Будет ли она копией предыдущей? Уверен, что нет. Разница будет связана именно с тем, что снилось Творцу.
Вот мы и подошли к финалу нашего изложения. Многое не сказано, многое осталось за кадром. Прошу извинить читателя, если моя концепция не вписывается в его мировоззрение. Каждая точка зрения имеет право на существование, поскольку на всё воля Божья.
Трехмерный мир, в котором мы не живем
Еще древние греки превратили математику из эмпирической науки в дедуктивную, потребовав вывода доказательств ее утверждений из основных понятий и исключив ссылку на опыт в качестве аргумента.
Чистая математика исследует формы и отношения в отвлечении от материального содержания. Ее непосредственным предметом оказываются, например, не те или иные тела шарообразной формы, а «идеальный шар», не те или иные совокупности предметов и даже не отдельные числа, а целые числа вообще и т. п.
Однако при всей абстрактности этой науки никто из математиков, по-видимому, не сомневался в том, что все их понятия, теоремы и формулы выражают реальные количественные и пространственные отношения. Математическая геометрия была теорией реального пространства, как позже механика явилась теорией движения
Математика — наука, изучающая
количественные и пространственные
формы и отношения действительности
Академик А. Д. Александров
Окружающий нас мир трехмерен. Мы привыкли к этой мысли с рождения — каждый человек знает, что такое высота, длина и ширина, три основных измерения окружающего нас пространства. В зависимости от традиций, принятых в разных странах, размеры предметов измеряют в метрах, футах, ли, лье и других эталонных единицах длины. Для наших дальнейших рассуждений выберем немного необычную единицу длины. Ею будет служить один световой год (1 св. г.), т. е. расстояние, проходимое лучом света за один календарный год. В традиционных мерах длины это составляет невообразимую величину — примерно 9,46•10 12 километров.
Если из окружающего нас пространства мысленно вырезать куб с ребром, равным 1 св. году, то внутри благополучно разместится дом, в котором мы живем, земной шар, Солнечная система… В общем, все, что необходимо для нормальной жизни человека. Для удобства назовем рассмотренный нами куб единичным кубом. А теперь отметим следующий очевидный факт. Несмотря на громадные размеры, наш единичный куб — лишь мельчайшая частица окружающего мира.
Кстати сказать, в этом определении размеры самого куба не задаются — вовсе не обязательно использовать кубы больших размеров. С таким же успехом можно утверждать, что каждая точка содержится в кубе, ребро которого не превосходит по длине, скажем, один микрон (10 —6 см).
Все сказанное выше кратко можно выразить следующими словами: окружающий нас мир является трехмерным евклидовым многообразием. А теперь попробуем ответить на следующий вопрос: как устроен мир за пределами единичного куба, в котором находится наш дом — наша Солнечная система?
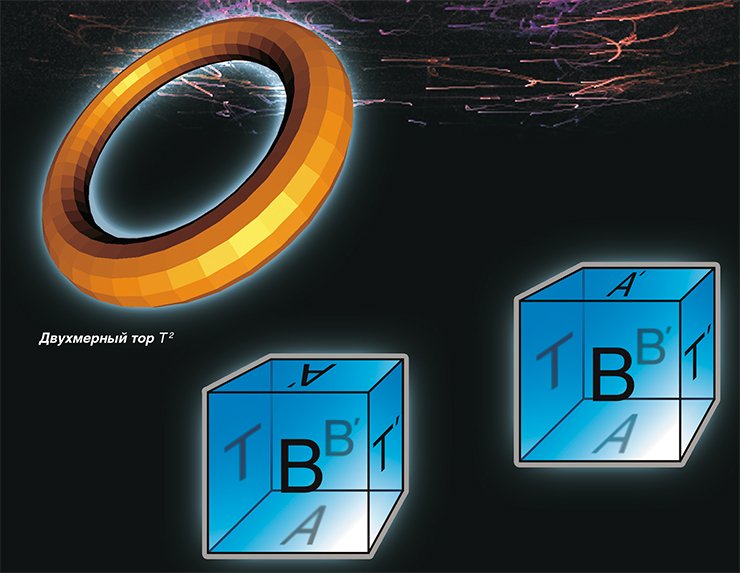
Трехмерный тор и другие
Если на минуту вообразить, что окружающее нас пространство бесконечно по всем направлениям, то ответ на вопрос о строении окружающего нас мира даст следующая теорема Адамара:
«Бесконечно протяженное по всем направлениям трехмерное евклидово многообразие М 3 совпадает с евклидовым пространством E 3 ».
Евклидово пространство Е 3 с прямоугольной системой координат всем хорошо известно, поэтому не будем подробно останавливаться на изучении его свойств.
Для того же, чтобы сделать наши рассуждения более содержательными и интересными, предположим другой вариант: окружающий нас мир замкнут, т. е. имеет конечные размеры и не имеет края. Другими словами, зададимся вопросом, как устроены замкнутые трехмерные евклидовы многообразия, или, другими словами, евклидовы формы. Полный ответ на этот вопрос дает теорема, доказанная Дж. Вольфом (1982):
Существует ровно десять трехмерных евклидовых форм. Причем шесть из них представляют собой ориентируемые, а остальные четыре — неориентируемые многообразия.
Все евклидовые формы строятся схожим образом, единственное — для построения некоторых из них нужно использовать куб, а для других — правильную шестиугольную призму.
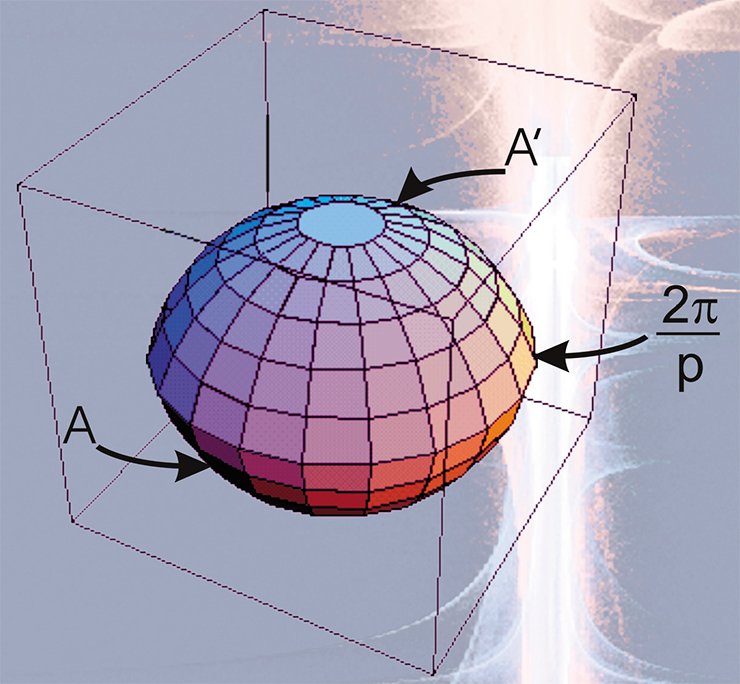
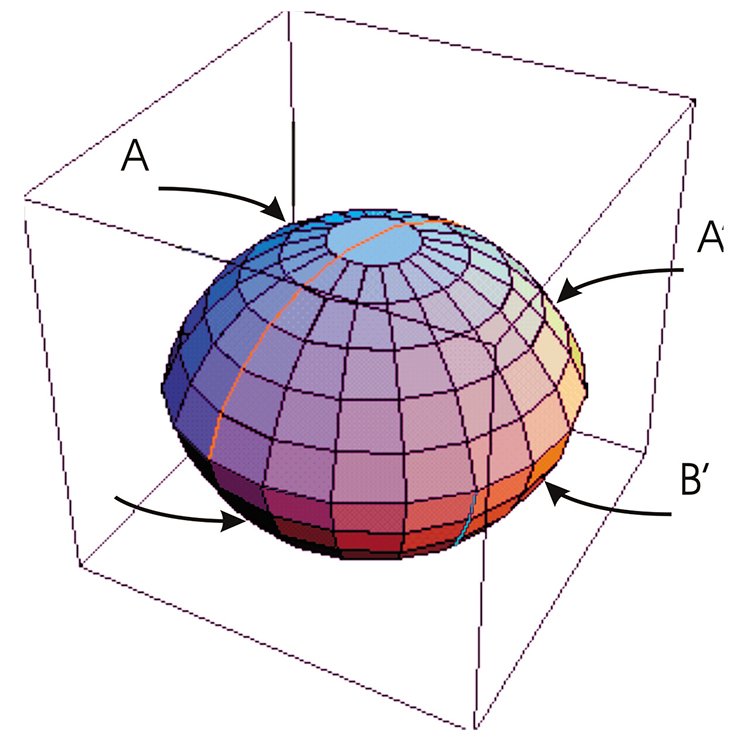
Для этого в центре грани А трехмерного тора поместим космический корабль, летящий со скоростью света, и заставим его стартовать в вертикальном направлении. Ровно через год космический корабль, продолжая двигаться по прямой, вернется в исходную точку. Теперь эта точка будет находиться в центре грани А’, которая, по условию, отождествлена с гранью А. В результате эксперимента обнаружим, что в трехмерном торе Т 3 существует замкнутая прямая линия l длиной в один световой год.
Поставим еще один аналогичный эксперимент. Заставим космический корабль стартовать из точки у, лежащей в грани А на расстоянии 1 км от ее центра. Через год корабль благополучно вернется в точку у. Вывод из второго эксперимента — через точку у проходит замкнутая прямая длиной 1 световой год, параллельная прямой l.
Многообразные многообразия
Как уже было замечено, все рассмотренные выше многообразия обладают евклидовой геометрией. Что это означает и какие еще геометрии существуют?
Наиболее известными и употребимыми в общечеловеческой практике являются евклидова, сферическая и гиперболическая геометрии. Напомним, что сферическую геометрию иногда называют геометрией Римана, а гиперболическую — геометрией Лобачевского. В трехмерном пространстве, кроме трех указанных, существует еще пять так называемых синтетических геометрий.
В соответствии с тем, какие геометрические законы действуют на трехмерном многообразии, будем называть его соответственно евклидовым, сферическим, гиперболическим или синтетическим.
Евклидовы многообразия мы уже рассмотрели выше. Что до остальных, то более двадцати лет назад У. Терстон (1978) доказал замечательную теорему: почти все трехмерные многообразия являются гиперболическими, то есть подчиняются законам геометрии Лобачевского. За этот результат в 1983 году он был удостоен Филдсовской премии — самой престижной награды для математиков.
Сферические многообразия бывают как трехмерные, так и многомерные (Вольф, 1982). В пространстве любой размерности существует конечное число типов таких многообразий. Синтетических многообразий очень мало (Thurston, 1978; Dunbar, 1981; Терстон, 2001) в отличие от оставшегося класса гиперболических многообразий. Последний неисчерпаемо широк и классификация его к настоящему времени не завершена.
Сферические многообразия
Все трехмерные сферические многообразия — ориентируемы. Это означает, что по какой бы замкнутой траектории не летал космический корабль с непрерывно вращающимся пропеллером, по возвращении в точку старта его пропеллер вращается в ту же сторону, что и в момент старта.
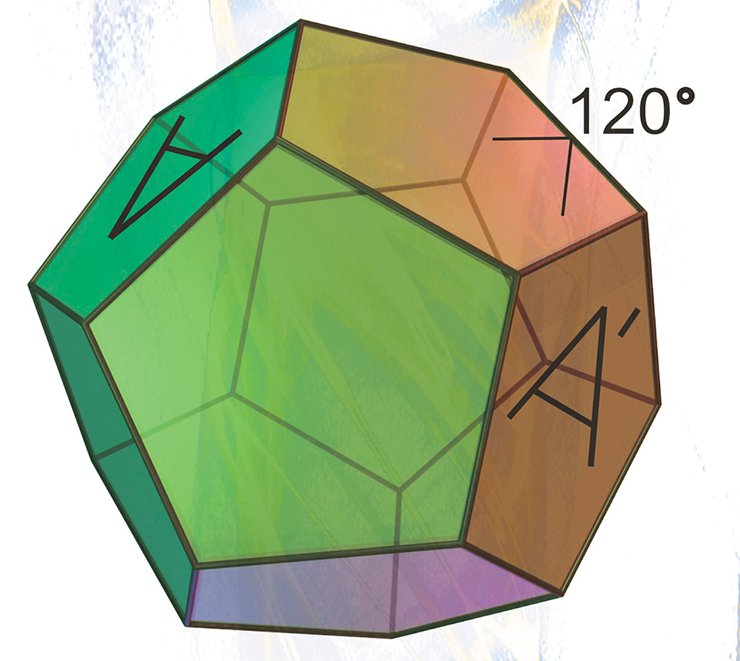
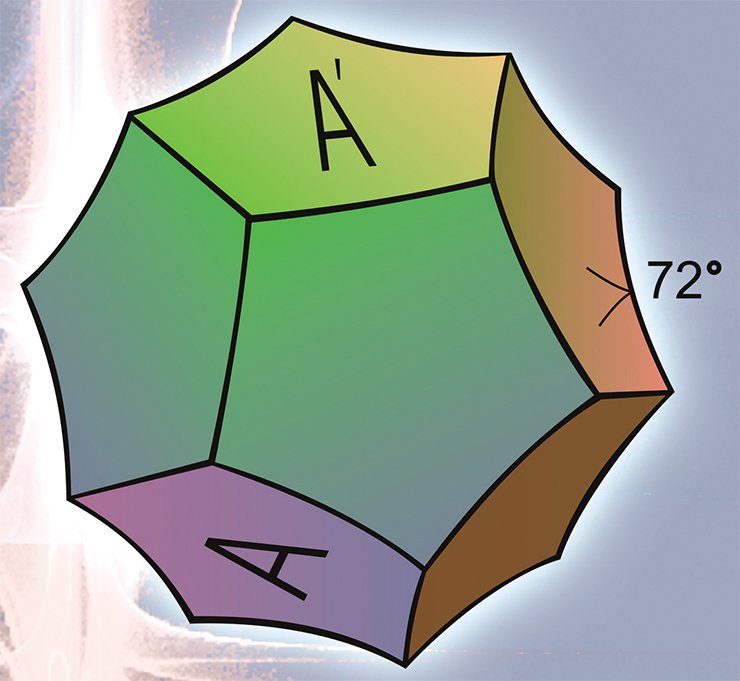
Третий, и пожалуй, самый нетривиальный пример сферического многообразия — сферическое пространство додекаэдра Пуанкаре или, для краткости, сфера Пуанкаре.
Сфера Пуанкаре удивительным образом связана с самыми различными разделами математики — геометрией, топологией, теорией групп, теорией катастроф, теорией узлов и другими (Кирби, Шарлеман, 1982).
Все остальные сферические многообразия, получаемые по единой схеме, представляют собой так называемые линзовые и призматические пространства.
Гиперболические многообразия
Первое трехмерное замкнутое гиперболическое многообразие было построено немецким математиком Ф. Лебеллем в 1931 г. Однако построение его было достаточно сложным, поэтому двумя годами позже Х. Зейферт и К. Вебер предложили элегантную конструкцию гиперболического пространства додекаэдра.
С точки зрения математики наиболее сложная часть проблемы построения состоит в доказательстве существования этого гиперболического додекаэдра в пространстве Лобачевского. Положительный ответ на этот вопрос дает фундаментальная теорема Е. М. Андреева (1970), в которой сформулированы необходимые и достаточные условия для существования выпуклых гиперболических многогранников. Эта теорема служит одним из краеугольных камней современной теории гиперболических многообразий, созданной У. Терстоном.
Конструируем многообразия из многогранников
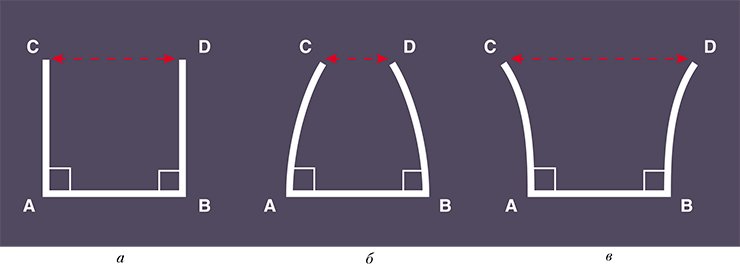
Рассмотрим прямоугольный многогранник Р, все двугранные (и плоские) углы которого равны 90°. В евклидовом пространстве в качестве такого многогранника можно взять куб, в сферическом — тетраэдр, а в гиперболическом — шестиугольную призму Лебелля, боковая поверхность которой состоит из 12-ти пятиугольников.
Из теоремы Андреева следует, что любой многогранник, у которого нет треугольных и четырехугольных граней, а в каждой вершине сходится ровно по три ребра, может быть реализован как прямоугольный многогранник в пространстве Лобачевского. Шестиугольная призма Лебелля, очевидно, удовлетворяет этим условиям.
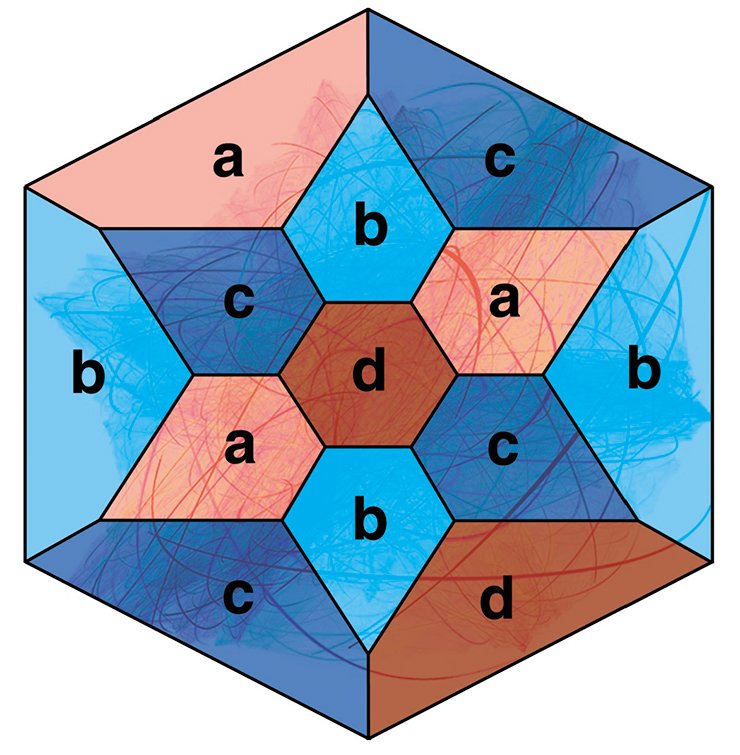
Для построения гиперболических многообразий используется способ, заключающийся в окраске смежных граней многогранника в разные цвета и последующего отождествления соответствующих граней, окрашенных в один цвет, у нескольких одинаковых экземпляров многогранников. Такой способ построения многообразий был впервые реализован Ф. Лебеллем (Loebell, 1931) для шестиугольной призмы, японским математиком М. Такахаши (Takahashi, 1985) — для правильного прямоугольного додекаэдра и А. Ю. Весниным (1987) — для произвольного прямоугольного многогранника Р.
При этом отметим, что все многообразия, построенные по окраске многогранника в четыре цвета, ориентируемы. Однако доказано, что окрашивая грани многогранника Р в пять, шесть или семь цветов, по аналогичной схеме можно построить и неориентируемые многообразия (Mednykh, 1992).
Остановимся еще на одном свойстве прямоугольных многогранников. Пусть D — правильный прямоугольный додекаэдр в пространстве Лобачевского. Испанский математик Х.-М. Монтезинос (Hilden et al., 1987) доказал следующую замечательную теорему:
«Любое замкнутое трехмерное многообразие может быть получено из конечного числа экземпляров многогранника D попарным отождествлением их граней».
Отметим, что в теореме Монтезиноса все грани склеенных многогранников — конгруэнтны, а все ребра имеют одинаковую длину. При этом каждое ребро окружено четырьмя, двумя или одним додекаэдром. Первую ситуацию легко представить: четыре прямоугольных додекаэдра склеены друг за другом вокруг общего ребра и образуют суммарный угол, равный 4•90° = 360°. Во втором случае пара смежных граней одного додекаэдра отождествляется с парой смежных граней другого додекаэдра. Суммарный двугранный угол вокруг ребра, принадлежащего двум додекаэдрам, в этом случае равен 2•90° = 180°. Третий вариант легко создать, отождествляя смежные грани одного додекаэдра поворотом на угол 90°.
Наличие ребер второго и третьего типа превращает многообразие в многообразие с особенностями, или орбифолд. В этом случае указанные ребра образуют сингулярное множество орбифолда. Заметим, что всюду, кроме сингулярных ребер, многообразие обладает геометрией Лобачевского.
Трехмерные орбифолды
Евклидовы орбифолды
Для всякого трехмерного евклидова орбифолда существует фундаментальное множество — криволинейный многогранник, из которого заданный орбифолд можно получить, попарно отождествляя (склеивая) определенные его грани.
Примерами евклидовых орбифолдов могут служить так называемые Борромеевы кольца или трехмерная сфера с сингулярным множеством узел «восьмерка».
Всего существует 230 замкнутых трехмерных евклидовых орбифолдов — по числу кристаллографических групп, открытых в конце прошлого века русским ученым Е. С. Федоровым. Строение евклидовых орбифолдов было полностью описано в докторской диссертации У. Данбара, защищенной в 1981 г. в Принстонском университете — крупнейшем математическом центре мира.
Сферические орбифолды
Сингулярным множеством сферических орбифолдов может служить так называемый рациональный узел или зацепление. Им может оказаться также заузленный граф, из каждой вершины которого выходит по три ребра. В частности, сингулярным множеством сферического орбифолда будет являться скелет тетраэдра (ребра + вершины), расположенный в трехмерной сфере.
q > l. В сферическом пространстве S ³ рассмотрим линзу с углом, равным π/р и поделим ее ребро точками 1,2. 2р на 2р равных частей. Соединим пары точек <р, 2р>и
При этом следует иметь ввиду, что сильные заузливания тетраэдра могут испортить сферическую геометрию и заставить орбифолд обладать евклидовой, гиперболической или одной из синтетических геометрий.
Недавно австралийцами профессором К. Ходжсоном и его учеником Д. Хеардом создана компьютерная программа, позволяющая вычислять объемы заузленных графов, вложенных в трехмерную сферу (Hodgson and Heard, 2005). Полная классификация трехмерных орбифолдов во всех геометриях, кроме гиперболической, сделана в работах У. Данбара. Как и в случае многообразий, гиперболическая геометрия является наиболее богатой, и полное описание орбифолдов в ней до сих пор не получено.
Гиперболические орбифолды
Из теоремы Монтезиноса следует, что каждое трехмерное многообразие может быть превращено в гиперболический орбифолд, если внутрь его поместить подходящее сингулярное множество. Поскольку существует бесконечно много различных многообразий, отсюда следует, что существует также бесконечно много гиперболических орбифолдов.
Один из простейших гиперболических орбифолдов — трехмерная сфера с сингулярным множеством Борромеевы кольца с индексом сингулярности 4. Другой пример — сильно заузленный тетраэдр, все ребра которого имеют индекс сингулярности два. Доказательство таких фактов обычно достаточно сложно и может быть проведено с помощью теорем о геометризации, полученных У. Терстоном, его учениками и последователями. Общий принцип доказательства состоит в следующем: если орбифолд не является евклидовым, сферическим или синтетическим и удовлетворяет некоторым простым геометрическим условиям, то он — гиперболический.
Изменения, произошедшие в математике за последние более чем полтора века, не только необозримо расширили ее содержание, но и изменили его принципиально. В предмет математики сейчас входит любая структура, которую можно исследовать путем логического рассуждения с достаточной строгостью и богатством выводов. Найдет ли она применение и прообраз в действительности — это уже вопрос не к математике.
Понятно, что фактически наибольшее развитие получают те теории, которые находят существенные применения в самой математике и тем более за ее пределами. Хотя опыт развития науки уже достаточное число раз показал, как самые отвлеченные теории находили потом чрезвычайно существенные приложения. Но для самой чистой математики это в принципе безразлично. Лучше всего творческое кредо новой математики выразил создатель теории множеств Г. Кантор, гордо зявив: «Сущность математики. в ее свободе».
Винберг Э. Б. О неевлидовой геометрии, Соросовский образовательный журнал, № 3, 1996, С. 104—109.
Тёрстон У. Трехмерная геометрия и топология, М: МЦНМО, 2001 (Перевод с англ. под ред. О. В. Шварцмана).
Hodgson C., Heard D. Computer program “Orb”, August 2005, http://www.ms.unimelb.edu.au/
Работа поддержана грантом РФФИ (№ 06-01-00153) и INTAS (№ 03-01-3663)
Автор и редакция выражает искреннюю благодарность Н. В. Абросимову (вед. инженеру Института математики им. С. Л. Соболева СО РАН, студенту 6-го курса НГУ), оказавшему неоценимую помощь при подготовке публикации