с какого дня должен начаться месяц чтобы 13м числом была пятница
С какого дня должен начаться месяц чтобы 13м числом была пятница
Артур ты можешь хоть для прикол флиртовать с бабами ото всегда ты с вопросами жгешь серзно)?
Да но тут как не хоти это не вазможно я имел ввивуду для мозгу разнабразю
Продолжай дела твое я ответ получил
А после полуночи зеркало какого обьема должно быть,чтобы посмотреть
вот в мае этого года и посмотри
Она и есть, пятница 13е
Не знаю. а подсказки есть?
Блииин,тупею на глазах. могла бы просто немного подумать)))
Ну, а май начинает с воскресенья, специально в календарь залезла. ))
Да и в мае нам повезло
Дело в том что от нас далеко не всё зависит. Например погода. Или политическая ситуация. Возможно ваш талант видеть во всём позитив и устраивать вокруг себя окружающую среду, делает вам честь. Но если не замечать тенденций на ухудшение, не как их не отменяет. Я хотел бы с вами согласится но, увы.
Ну что ж замечательно. У тебя есть зонтик. Удачи.
Путеводитель по календарю или ликбез для не особо продвинутых
«В июле 2011 5 пятниц, 5 суббот, 5 воскресений. Такое бывает раз в 823 года»
Наверняка, вы не раз уже встречали подобные «откровения» в интернете, в первую очередь в твиттере. Пару раз в году обязательно начинается флуд на тему того, какое это редкое событие — 5 пятниц, суббот и воскресений в одном месяце.
Причина этой радости прекрасно понятна — ведь, выходит, в этом месяце больше, чем обычно, выходных и дней, в которые принято напиваться! Вот только запаздывает осознание того, что от этого таких дней в году больше не становится.
Но меня возмущает не флуд и беспричинная радость, а глупость утверждения о том, что это настолько редкое событие, что случается раз в 823 года. Все повторяют это друг за другом как попугаи, даже не задумываясь о корректности данного утверждения. А тем временем это откровеннейший бред, ведь такие месяцы выпадают часто, намного чаще, чем твердят недалекие «знатоки» календаря.
В прошлый раз, когда такое событие произошло, я выместил свою злость и ярость на одного неплохого человека, с которым в результате этого больше не общаюсь. Но впредь я решил этой ошибки не повторять, а написать небольшую статью-ликбез, к которой буду отсылать теперь всех попугаев.
Координаты чудес
Для начала давайте рассмотрим, что же за особенный месяц такой, в котором по 5 пятниц, суббот и воскресений. Для примера возьмем все тот же июль 2011 года:
Как нетрудно заметить, 5 пятниц, суббот и воскресений в одном месяце (будем называть такие месяцы «волшебными») может быть только при выполнении двух условий:
Копаем глубже
Более того, день, с которого начинается тот или иной месяц, зависит только от того, с какого дня недели начинается год, и является ли этот год високосным (для всех месяцев кроме января). Для каждой пары «год/високосный год — месяц» смещение по разнице в днях недели постоянно. Смотрите таблицу:
Собственно, смещение это накапливается с каждым месяцем и равно остатку от деления на 7 числа дней в каждом месяце (январь — 3, февраль — 0 или 1, март — 3 и т. д.). То есть, смещение составляет 3 дня для каждого месяца из 31 дней, 2 дня для месяцев из 30 дней и 0/1 день для февраля, который у нас такой особенный (1 для високосного года).
Обратите внимание, что смещение выводится в виде остатка от деления на 7 (т.е. имеем кольцо классов вычетов по модулю семь).
| Месяц | Месячное смещение | Месячное смещение (вис.) | Смещение с начала года | Смещение с начала года (вис.) |
|---|---|---|---|---|
| январь | 3 | 3 | 0 | 0 |
| февраль | 0 | 1 | 3 | 3 |
| март | 3 | 3 | 3 | 4 |
| апрель | 2 | 2 | 6 | 0 |
| май | 3 | 3 | 1 | 2 |
| июнь | 2 | 2 | 4 | 5 |
| июль | 3 | 3 | 6 | 0 |
| август | 3 | 3 | 2 | 3 |
| сентябрь | 2 | 2 | 5 | 6 |
| октябрь | 3 | 3 | 0 | 1 |
| ноябрь | 2 | 2 | 3 | 4 |
| декабрь | 3 | 3 | 5 | 6 |
Обратите внимание, что по результатам года общее смещение будет 1 для обычного года и 2 для високосного, что полностью соответствует действительности — остаток от деления 365 на 7 равен 1, а остаток от деления 366 — 2.
Извлекаем истину на свет
Итак, у нас есть результат, который мы хотим получить — нам нужно, чтобы месяц начинался с пятницы. Смещение от начала года нам известно, поэтому легко определить, с какого дня должен начинаться год для каждого из месяцев, чтобы этот месяц стал «волшебным».
Следующая таблица вытекает из предыдущей (тут нас уже интересуют только 7 месяцев). Т. е., для каждого месяца получаем день недели, с которого должен начинаться год, чтобы этот месяц был «волшебным»:
| Месяц | Искомое начало года | Искомое начало года (вис.) |
|---|---|---|
| январь | пятница | пятница |
| март | вторник | понедельник |
| май | четверг | вторник |
| июль | суббота | пятница |
| август | среда | вторник |
| октябрь | пятница | четверг |
| декабрь | воскресенье | суббота |
Можете убедиться, этот год начался в субботу и не является високосным, поэтому июль стал «волшебным».
Выходит, что такие месяцы есть практически в каждом году:
| Начало года | «Волшебные» месяцы | «Волшебные» месяцы (вис.) |
|---|---|---|
| понедельник | — | март |
| вторник | март | май, август |
| среда | август | — |
| четверг | май | октябрь |
| пятница | январь, октябрь | январь, июль |
| суббота | июль | декабрь |
| воскресенье | декабрь | — |
Получается, «волшебные» месяцы — не такая уж и редкость. Бывает даже по два таких месяца за один год. Хотя иногда бывает и такое, что за весь год нет ни одного такого месяца.
Раз в 823 года
Рассмотрим теперь тезис о том, что «волшебный» июль случается раз в 823 года. Как мы уже показали, такой июль случается каждый не високосный год, который начинается с субботы. Неужели это такая редкость — год, начинающийся с субботы? Здравый смысл подсказывает нам, что это обычное дело, а учитывая смещение на 1 день недели каждый год (и на 2 каждый високосный), случаться такое должно примерно раз в 7 лет.
Не будем рассматривать все прошлые и будущие годы, просто взглянем на годы с 2000 по 2022 (ниже поймете, почему именно эти):
| Год | Начало | Смещение |
|---|---|---|
| 2000 (вис.) | суббота | 2 |
| 2001 | понедельник | 1 |
| 2002 | вторник | 1 |
| 2003 | среда | 1 |
| 2004 (вис.) | четверг | 2 |
| 2005 | суббота | 1 |
| 2006 | воскресенье | 1 |
| 2007 | понедельник | 1 |
| 2008 (вис.) | вторник | 2 |
| 2009 | четверг | 1 |
| 2010 | пятница | 1 |
| 2011 | суббота | 1 |
| 2012 (вис.) | воскресенье | 2 |
| 2013 | вторник | 1 |
| 2014 | среда | 1 |
| 2015 | четверг | 1 |
| 2016 (вис.) | пятница | 2 |
| 2017 | воскресенье | 1 |
| 2018 | понедельник | 1 |
| 2019 | вторник | 1 |
| 2020 (вис.) | среда | 2 |
| 2021 | пятница | 1 |
| 2022 | суббота | 1 |
Таким образом, с субботы начинаются 2000, 2005, 2011 и 2022 годы, но 2000 високосный, поэтому он нам не подходит. Но даже при этом примерно за 20 лет трижды встречается «волшебный» июль. Можете в этом убедиться сами, посмотрев на календарь.
Так что, можете теперь с легкостью «предсказать», какие в скором времени будут «волшебные» месяцы. И не пишите, пожалуйста, бред о том, что это случается раз в 823 года. И не делайте ретвит!
С какого дня должен начаться месяц чтобы 13м числом была пятница
a) Почти все годы XIX века записываются так: 18.. (исключение — 1900 год, который нам, очевидно, не подходит). Поэтому, чтобы год читался одинаково справа налево и слева направо, оставшиеся две цифры должны быть 81.
Заметим, что в каждом году может быть не более одной даты-палиндрома. Действиетельно, если уже написан номер года (например, 2012), то число и месяц даты-палиндрома в этом году звписываются теми же цифрами в обратном порядке (в нашем примере 21.02). То есть по номеру года дата-палиндром (если она есть) определяется однозначно.
Таким образом, в 2012 году нет дат-палиндромов, кроме указанной. Попробуем найти предыдущую дату-палиндром в 2011 году. Это будет 11.02.2011.
Следующая дата-палиндром будет не раньше 2013 года. Попробуем найти такую дату в 2013 году. Но это может быть только 31.02.2013, а такой даты нет, поскольку в феврале 2013 года всего 28 дней. Значит, в 2013 году дат-палиндромов не будет. По аналогичным причинам дат-палиндромов не будет и с 2014 по 2019 год. А вот в 2020 году дата-палиндром найдётся: это будет 02.02.2020.
a) Пять понедельников всегда будет в месяце, начинающемся с понедельника (если только это не февраль невисокосного года). Шести понедельников в одном месяце быть не может. Действительно, тогда в таком месяце было бы как минимум пять полных недель и ещё один понедельник, то есть не менее 7·5+1=36 дней, а такого не бывает.
b) 365 = 52·7 + 1, 366 = 52·7 + 2. Поэтому в каждом году не более 52 полных недель (от понедельника до воскресенья). Если год начинается с понедельника, то каждая из 52 полных недель будет начинаться с понедельника, а 31 декабря тоже будет понедельником. Поэтому в этом случае в году будет 53 понедельника. А если бы в каком-то году было хотя бы 54 понедельника, то в нём было бы не меньше 53 полных недель, чего быть не может.
Часть II
Часть III
Выпишем номера дней года, на которые попадают 13-е числа разных месяцев. 13 января, очевидно, будет тринадцатым днём года. 13 февраля будет 31+13=44-м днём года, 13 марта будет 31+28+13=72-м днём года (будем пока считать, что наш год невисокосный). Далее аналогично находим: 13 апреля — 103-й день, 13 мая — 133-й день, 13 июня — 164-й день, 13 — июля 194-й день, 13 августа — 225-й день, 13 сентября — 256-й день, 13 октября — 286-й день, 13 ноября — 317-й день, 13 декабря — 347-й день. (Номера тринадцатых чисел в високосном году посчитайте самостоятельно.)
Посмотрим на остатки от деления этих номеров на 7. Получим: 6, 3, 2, 5, 0, 3, 5, 1, 4, 6, 2, 4 (проверьте!). Для високосного года эти остатки будут равны, соответственно, 6, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5. Заметим, что в обоих списках встречаются все возможные остатки от деления на 7 (от 0 до 6).
Номера всех дней года, приходящихся на пятницу, имеют один и тот же остаток от деления на 7 (так как пятница бывает раз в 7 дней). Кроме того, все дни года, номера которых дают одинаковый остаток при делении на 7, приходятся на один и тот же день недели (потому что в неделе 7 дней). Как мы выяснили, номера дней года, приходящихся на 13-е числа разных месяцев, дают все возможные остатки от деления на 7. Поэтому, какой бы остаток от деления на 7 ни давали номера пятниц, всегда найдётся 13-е число какого-нибудь месяца, номер которого делится на 7 с тем же остатком. Это и будет «пятница 13-е».
Пятница – всегда 13-е. Нужен ли нам еще один месяц в году?
Идея календаря на 13 месяцев может показаться нам смешной и глупой, однако по своей логике данный календарь немногим отличается от григорианского, которым мы пользуемся сейчас, и даже использовался в качестве корпоративного календаря крупной американской компании в течение 65 лет. «Футурист», отрицая все суеверия, объясняет, зачем нам дополнительный, тринадцатый, месяц в году.
Почему в некоторых месяцах 30 дней, в других 31, а в одном особенном случае – вовсе 28? Несмотря на кажущуюся очевидность вопроса, многие могут быть всерьез им озадачены. Так, например, британец Мозес Б. Котсворт еще в 1902 году предложил свою версию календаря на 13 месяцев.
На рубеже 20-го века Мозес Б. Котсворт, бухгалтер Британской железнодорожной компании, увлекся усовершенствованием календаря. Проблема, которая его волновала, вполне понятна: каждый месяц имеет разное количество дней и недель, и слишком многое меняется каждый год. Придуманный Котсвортом календарь состоит из 13 месяцев ровно по 28 дней. Каждый месяц имеет четыре недели, и каждый день соответствует определенному дню недели: первое число всегда воскресенье, а 13-е, что интересно, всегда пятница. 13-й месяц Котсворта назван Сол, в честь летнего солнцестояния, так как находится между июнем и июлем, когда и происходит солнцестояние. Високосный день был также перемещен с конца февраля на конец сола. Чтобы довести год до 365 дней, Котсворт добавил День Года после 28 декабря как глобальный праздник, не относящийся ни к одному конкретному месяцу.
Однако, несмотря на все попытки Котсворта приспособить к использованию своего календаря более авторитетных фигур, никто не уделил особого внимания его идее, кроме одного человека: основателя Kodak Джорджа Истмана. Kodak внедрил 13-месячный календарь в 1924 году, и он оставался в действии, организовывая финансы и производство компании, вплоть до 1989 года. Хотя 13-месячный календарь может показаться нам странным, он не является более необычным, чем григорианский календарь, который мы используем сегодня и который прошел через множество изменений, чтобы оставаться на протяжении тысячелетий следовать графику.
Изначально древние египтяне использовали ярчайшую звезду Сириус для предсказания ежегодного наводнения Нила, что позволило им стать одной из первых цивилизаций, начавшей использовать солнечный календарь вместо лунного. Однако даже сейчас мусульманские и еврейские календари базируются на движении Луны. Сохранение этой традиции, впрочем, связано с некоторыми трудностями: лунный месяц длится 29.5 дней, то есть 12 месяцев составляют 354 лунных дня, что примерно на 11 дней короче солнечного года. Для решения этой проблемы, в некоторые лунные календари, например, еврейские, периодически добавляют лишний месяц.
Египтяне же, благодаря Сириусу, смогли свести год к 12 месяцам и 5 дополнительным дням в конце года, и на этом, казалось бы, вопрос был исчерпан. Но каждые четыре года Сириус появляется на день позже положенного, так как солнечный год составляет примерно 365 дней и шесть часов, что в Древнем Египте не учитывали.
Далее Юлий Цезарь решил исправить отстающий к тому времени уже на три месяца календарь и ввел новый, более точный Юлианский календарь 1 января 45 г. до н.э. Используемый же нами до сих пор григорианский календарь получил свое название в честь папы римского Григория, который потребовал усовершенствовать прежний календарь. Дело в том, что продолжительность года на самом деле составляла чуть менее 365 и шести часов, таким образом, юлианский календарь насчитывал 10 лишних дней на момент введения григорианского календаря. Переход к новому календарю был связан с активным сопротивлением во многих странах. Интересно, что так как в России григорианским календарем стали пользоваться лишь после революции 1917 года, российская сборная опоздала на летние олимпийские игры 1908 года в Лондоне на 12 дней.
Сколько раз в году 13-ое число может выпадать именно на пятницу?
Бывают ли года вообще без такой даты?
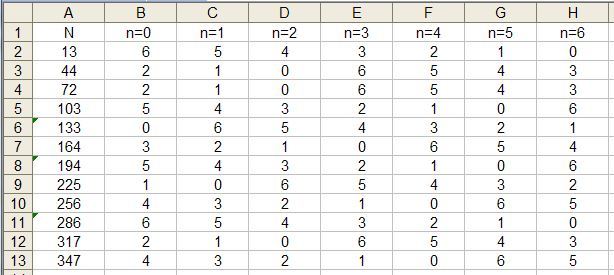
Сначала вычислим порядковые номера дней в месяцах, приходящиеся на
13-ое число. Они приведены в первой колонке таблицы под заголовком N.
Далее, так как год может начинаться с неполной недели, и до первой
пятницы может пройти от 0 до 6 дней (в таблице это значение n), то
разница N-n должна нацело делиться на 7, т.е. давать в остатке 0,
чтобы укладываться в целое число недель. В остальных колонках
показаны рез-ты вычисления этих остатков при всех возможных
значениях n. Как видим, независимо от дня начала года, не может
быть такого, который бы обошелся без хотя бы одной «черной» пятницы.
А в некоторые годы их может быть и не одна. Подтверждением является нынешний 2013,
начавшийся со вторника (n=4). В нем два таких месяца, в которых остаток
Разумеется, все вычисления приведены для не високосного года,
для високосного таблица будет выглядеть иначе, но ее легко составить
по указанному методу.
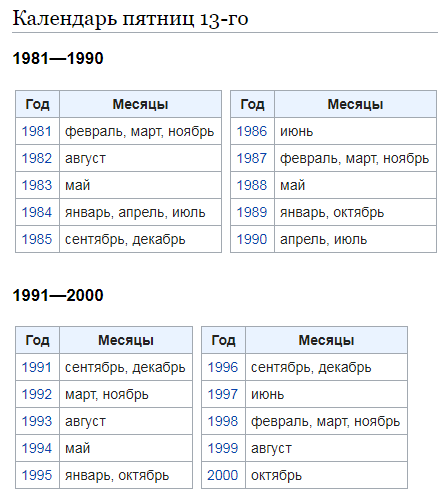
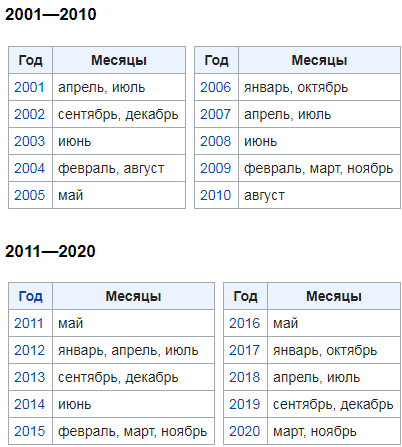
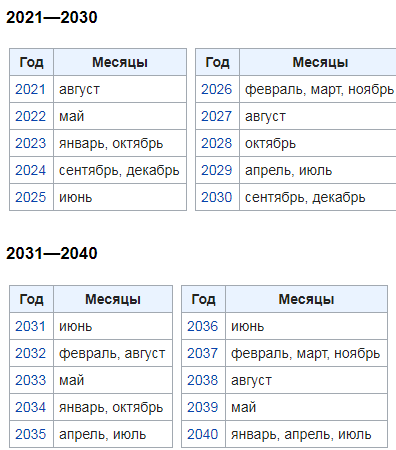
Количество пятниц 13 в году может быть разное. Это зависит от того, с какого дня недели начался год и високосный ли год на дворе)
Но всего в один год пятницы 13 может быть не более трёх. Чаще две, реже одна. Это видно по календарям.
Интересно, что люди с математическим складом ума (или просто любопытные от природы) по-разному пытаются вычислить сколько же раз в год встречается пятница 13.
На одном из форумов также задались этим вопросом и предлагали варианты вычислений) Причём каждый считал, что его подсчёты самые лёгкие и элементарные. А я бы со своим гуманитарным образованием в лучшем случае попыталась посмотреть по календарику.
Пятница тринадцатое, как часто выпадает такая дата?
Во-первых, нет ни одного такого года, в котором не было бы такой даты;
во-вторых, в год может быть одна «чёрная» пятница, две или три.
в-третьих, в месяце есть «пятница 13-ое», если месяц начинается с воскресенья.
Так же, как и Владимир 3, я составил таблицу, но учёл в ней ещё и наличие високосных годов.
Вообще, чтобы иметь календарь на любой год, достаточно 14-ти календарей: 7 календарей для обычных годов и 7, для високосных.
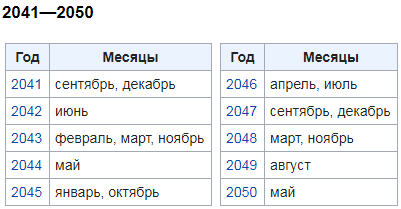
Вот такая таблица с «черными» пятницами получилась у меня ( красным помечены месяца, начинающиеся с воскресенья и соответственно, имеющие дату пятница 13-ое ):
По три «черные пятницы» бывает в обычные года, начинающиеся в четверг, и в високосные года, начинающиеся в воскресенье.
То есть легко можно подсчитать количество таких дней в году просто посмотрев по календарю, сколько месяцев начинаются с воскресенья.