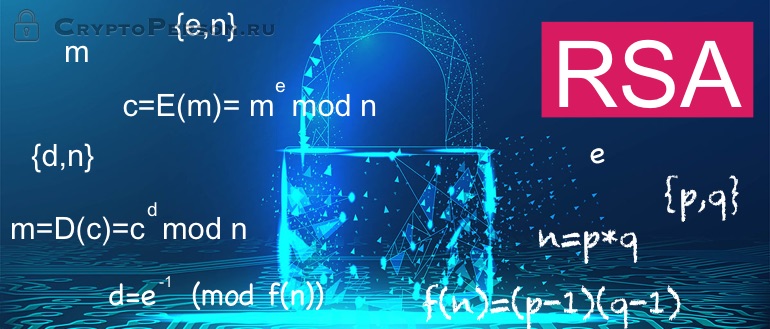
rsa private key что это
Rsa private key что это
Криптосистема [math]\mathtt
Содержание
Реализация [ править ]
Алгоритм [math]\mathtt
Криптографические системы с открытым ключом используют так называемые односторонние функции.
| Определение: |
| Односторонняя функция (англ. one-way function) — математическая функция, которая легко вычисляется для любого входного значения, но задача нахождения аргумента по заданному значению функции относится к классу NP-полных задач. |
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
Создание открытого и секретного ключей [ править ]
| Определение: |
| Случайное простое число (англ. random prime numbers) — в криптографии, простое число, содержащее в двоичной записи заданное количество битов. |
Передача ключей [ править ]
Шифрование [ править ]
Расшифрование [ править ]
Корректность схемы [math]\mathtt[/math] [ править ]
Действительно, для [math]\forall m \in \mathbb
Возможны два случая:
где второе тождество следует из теоремы Ферма.
[math]m^
\equiv m \pmod
[/math]
Таким образом, при всех [math]m[/math] выполняется равенство
[math]m^
[/math]
Аналогично можно показать, что:
[math]\forall m \in \mathbb Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования [math]e \cdot d \equiv 1 \pmod<\varphi(n)>,[/math] Система [math]\mathtt Наиболее используемым в настоящее время является смешанный алгоритм шифрования, в котором сначала шифруется сеансовый ключ, а потом уже с его помощью участники шифруют свои сообщения симметричными системами. После завершения сеанса сеансовый ключ, как правило, уничтожается. Алгоритм шифрования сеансового ключа выглядит следующим образом: Алгоритм [math]\mathtt При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля. RSA – один из методов шифрования, который нельзя назвать самым безопасным, так как был разработан более 40 лет назад. Повышенная безопасность новых технологий не мешает RSA использоваться и по сей день, например, для передачи зашифрованных ключей. Дата создания алгоритма RSA 1977 год. Аббревиатура придумана на основе фамилий разработчиков: R – Ривест, S – Шамир, A – Адлеман. Первый буквы и стали являться наименованием для шифрования и технологии в целом. Несмотря на дату официального создания, основа системы была разработана в 1973 году Клиффордом Коксом. Алгоритм английского математика использовался исключительно засекреченными лицами, технологию не предоставляли для обычных граждан. Работа RSA-шифрования основывается на генерации ключей. Пользователь создает публичный шифр, основанный на двух больших числах и вспомогательных значениях. Если код простейший, то прочесть сообщение с его помощью будет легко, но процедура усложняется, если генерируется длинный ключ. За время своего существования RSA-шифрование было вдоль и поперек изучено, поэтому метод не может считаться эффективным и безопасным. Алгоритм подразумевает, что для его использования потребуется затрачивать какое-то время, что является крупным минусом на сегодняшний день. Алгоритм цифровой подписи RSA применяется для передачи общих кодов доступа в виде шифра. С его помощью симметричный ключ, используемый для скрытия и чтения большого количества данных, достигает своего адресата. Сегодня в криптомире повсеместно используются асимметрические ключи благодаря разработкам Диффи и Хеллмана, представленными общественности в 1976 году. Но полученный общий код невозможно было использовать в полной мере, так как принципы факторинга еще не были до конца изучены. Разработки были продолжены троицей программистов, доработавших механизм функции, направляемой по одному адресату. Его главным плюсом являлась сложность раскодирования. Разработанная система ассиметричного шифрования впоследствии стала называться RSA. Пришедшая эра электронных документов повлекла за собой развитие соответствущих подписей. Они необходимы для признания документов официальными. Цифровая подпись является переводом данных на криптографический язык. Благодаря такой основе системе, подпись конфиденциальна. Вся содержащаяся информация сторонах надежно защищена. Электронная подпись и RSA– это неделимый союз, так как первый не может существовать без второго. В киберпространстве существует два вида ключей: публичный и приватный. Если первый доступен любому пользователю, то второй является средством защиты от получения данных третьими лицами. Благодаря RSA-шифрованию документ является зашифрованным, но доступ к нему может быть получен в любой момент. Расшифровка подписи для проверки происходит при помощи закрытого, а предоставление доступа к заверенному документу через открытый ключ. Процесс шифрования и дешифровки RSA использует метод возведения в степень (умножение определенное количество раз). Для практических приложений публичный ключ возводится в небольшую степень. Часто можно встретить ситуацию, когда группа устанавливает одну и ту же степень возведения с разными модулями. Это дает возможность ускорить дешифровку и проверку, если сравнивать с процессом шифрования и подписания. За основу можно взять условное число k, которым является количество битов. В таком случае требуемое количество шагов будет равно в зависимости от необходимых действий: Для ускорения проведения процедур на основе RSA постоянно применяются новые разработки. В качестве таковой мог стать способ «быстрого умножения», который позволял уменьшить число требуемых шагов для успешного и безопасного выполнения операции. БПФ (FFT) не прижилось, ведь для реализации требуется сложное ПО, а для быстрой работы понадобится сделать размер ключей идентичным. Важно! Сегодня алгоритм RSA проигрывает в скорости большинству альтернативных способов блокового шифрования. Так DES минимум в сто раз быстрее при аппаратной реализации. RSA – это изученный метод шифрования, который можно взломать несколькими способами. Самым эффективным является поиск закрытого ключа, который позволяет открыть информацию из открытого ключа. Позволяет получать всю информацию, которая была зашифрованной, также внедряться в код подписи, подделывая ее. Для проведения атаки необходимо найти сомножители общего модуля n – p и q. Благодаря данным p, q, e, хакер может без проблем получить частный показатель d. Основная трудность метода – поиск сомножителей. В основе безопасности лежит схема определения множителей, что позволяет создать задачу без эффективных вариантов решения. Система взлома работает не только для поиска n на основании d, но и в обратную сторону. Если потребуется использовать современное оборудование для вычислений, то оно не будет оказывать негативного влияния на безопасность криптосистемы, для чего потребуется увеличить размер ключа. При соединении эти два пункта (улучшенное оборудование и удлиненный ключ), то можно получить более стойкую систему. Метод используется в отношении одного ключа или нескольких, если в пределах идентичного мелкого показателя шифруется множество сообщений, каким-либо способом связанных между собой. Тогда злоумышленник получит доступ ко всей информации. Есть типы атак, которые направлены лишь на конкретное сообщение. Главным минусом является невозможность получить доступ ко всем сообщениям, которые шифруются одним ключом. Самый простой способ для получения информации из одного сообщения – атака по открытому тексту, который был зашифрован публичным ключом получателя. Это позволяет получить информацию о двух приватных ключах, которые будут сравниваться. Защитой от такого способа взлома могут послужить пара разных битов, располагаемых в конце. Существует альтернативный вид взлома одного сообщения. Пользователь отправляет идентичное сообщение 3-ем корреспондентам, где используется одинаковый показатель. Злоумышленник имеет возможность перехватить одно из сообщений для кражи интересующей информации. Для предотвращения атаки достаточно ввести разные случайные биты в каждом сообщении. Еще один способ взлома одного сообщения – создание зашифрованного текста, который отправляется пользователю. Если второй откроет и расшифрует сообщение, то злоумышленник получит доступ к расшифровке отдельных писем. Существуют атаки, которые направлены не на взлом криптосистемы, а для получения доступа через слабые места шифрования, которые по сути уже являются прямым вторжением в экосистему. Тогда слабость проявляется не у алгоритма, а у способа реализации. Если приватный ключ хранится в системе без наличия достаточной защиты, то хакер сможет его украсть. Для обеспечения максимальной безопасности необходимо не только учитывать базовые правила, но и генерировать ключ увеличенной длины. Для защиты шифрования должны использоваться устойчивые числа p и q. Они необходимы для выявления свойств, затрудняющих получение множителей. Одним из таких являются главные делители: p – 1 и p + 1. Это позволяет создать защиту от определения множителей различными методами, которые можно применять только в отношении небольших делителей. Использование устойчивых чисел даже закреплено в правилах некоторых стандартов, например, ANSI X9.31. Но разрабатывающиеся способы факторинга уже могут работать даже с устойчивыми цифрами и большими делителями. Одной из таких схем выступает алгоритм разложения на множители эллиптических кривых. Поэтому в отношении действий некоторых хакеров использование устойчивых чисел не сможет обеспечить достаточную безопасность. Важно! Если будут разработаны дополнительные способы факторинга, то в RSA можно будет увеличить количество символов в числе для усложнения задачи. При определении размера ключа требуется опираться от модуля n, являющегося суммой p и q, которые для корректной работы должны иметь примерно равную длину. Если модуль равен 524 битам, то приблизительный размер 262 бита. Так как p = M*(± ), то значения p и q можно без труда найти, если разность чисел небольшая. Такой ключ увеличивает безопасность, но вместе с этим замедляет алгоритм. Определение длины ключа опирается на оценку данных, которые должны быть зашифрованы, а вероятные угрозы (их частота и направленность) учитываются только после этого. Существует специальная RSA-лаборатория, рекомендующая 1024 бита. Но если потребуется защитить важную информацию, то длина ключей лучше всего увеличить в 2 раза. Если же информация совершенно не ценна, то хватит 768-битного ключа. Персональный ключ имеет срок действия, обычно он равен одному году. Это необходимо для периодической замены ключей для безопасности. Как только срок действия ключа истекает, то необходимо создать новый код, который должен соответствовать длине прошлого. В природе существует бесконечное множество простых чисел. Хотя количество символов в RSA-шифровании ограничено, количество возможных простых чисел все равно очень велико. Интересно! Ключ длиной 512 битов включает в себя 10 150 возможных значений. В реальности защищенная передача сообщений возможна при использовании двух криптосистем: RSA и DES. Алгоритм процесса: Работа шифрования заключается в трех этапах: RSA – это тот тип шифрования, который обеспечивает достаточную безопасность, но только при увеличении длины ключа, из-за чего замедляется проведение остальных операций. Алгоритм предназначен для простых операций, которые не требуют высокого уровня защиты. Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает. Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах. Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим. Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ. Теперь пара чисел Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться. Я получил ваши данные ( E=10 ), и у меня имеется закрытый ключ Обратите внимание на то, что открытый ключ не может расшифровать сообщение. А закрытый ключ я никому не говорил. В этом вся прелесть асимметричного шифрования. Заметьте, никто, кроме меня (даже вы!) не может расшифровать ваше сообщение ( E=10 ), так как ни у кого нет закрытого ключа. Постараюсь это показать на примере. Давайте разложим на множители число 360: Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5 Давайте теперь возьмём число 361. Тут нам придётся помучиться. При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время. Многие читатели спрашивают, как всё это применяется на практике. Давайте рассмотрим чуть более приближенный к жизни пример. Зашифруем и расшифруем слово «КРОТ», предложенное одним из читателей. А заодно, бегло рассмотрим, какие проблемы при этом встречаются и как они решаются. Сперва сгенерируем ключи с чуть бо́льшими числами. Они не так наглядны, но позволят нам шифровать не только числа от нуля до 20. Оттолкнёмся от пары простых чисел Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19. Мы можем зашифровать каждое из этих чисел открытым ключом На самом деле, изложенный способ шифрования очень слаб и никогда не используется. Причина проста — шифрование по буквам. Одна и та же буква будет шифроваться одним и тем же числом. Если злоумышленник перехватит достаточно большое сообщение, он сможет догадаться о его содержимом. Сперва он обратит внимание на частые коды пробелов и разделит шифровку на слова. Потом он заметит однобуквенные слова и догадается, как кодируются буквы «a», «и», «o», «в», «к»… Путём недолгого перебора, он вычислит дополнительные буквы по коротким словам, типа «но», «не», «по». И по более длинным словам без труда восстановит все оставшиеся буквы. Таким образом, злоумышленнику не придётся отгадывать ваши секретные ключи. Он взломает ваше сообщение, не зная их. Чтобы этого не происходило, используются специальные дополнительные алгоритмы, суть которых в том, что каждая предыдущая часть сообщения начинает влиять на следующую. Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие. На практике, в исходное сообщение специально добавляются случайные и бессмысленные буквы в начало. Чтобы даже по первому коду было невозможно ничего понять. Получатель просто отбрасывает начало сообщения. То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква. В реальной жизни всё ещё немного сложнее. Блоки, на которые бьётся сообщение длиннее одной буквы. Поэтому, сперва применяются алгоритмы выравнивания, потом алгоритмы разбиения на блоки с перепутыванием, и только потом применяется само RSA-шифрование. Получатель делает всё в обратном порядке: расшифровывает, «распутывает» блоки и отбрасывает ненужную информацию, добавленную просто для выравнивания (чтобы сообщение можно было разбить на целое число блоков). Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось. По умолчанию инженеры подключаются к сетевому оборудованию с помощью имени пользователя и пароля. По протоколу Telnet учетные данные пользователя передаются в открытом виде, а по протоколу SSH в зашифрованном. Чтобы не передавать секретную часть по сети, используется аутентификация по публичным ключам. При такой аутентификации публичный ключ пользователя заранее прописывается пользователю на оборудовании. Секретный ключ по сети не передается. Это руководство поможет вам быстро начать использовать публичные ключи для аутентификации при подключении к сетевому оборудованию по протоколу SSH. Руководство применимо как для Windows, так и для Mac OS X. Я постарался сделать его максимально простым и информативным. Оно не перегружено, но отвечает на основные вопросы: Кроме стандартной аутентификации по паролю (password/keyboard) в протоколе SSH существует также аутентификация по публичному ключу (RSA). Аутентификация с помощью RSA-ключей состоит из нескольких этапов: Документ Secure Shell Configuration Guide, Cisco IOS Release 15E: Secure Shell Configuration Guide, Cisco IOS Release 15E Попытка ввести данные DSA-ключа: Пару RSA-ключей можно создать с помощью различных утилит: SecureCRT, PuTTYgen или любым другим ПО. При создании ключа можно задать Passphrase (защита ключа с помощью пароля). SecureCRT → Tools → Create Public Key…: Чуть-чуть теории → кнопка “Next >”: Тип сертификата RSA/DSA → Выбираем RSA → кнопка “Next >”: Пароль шифрования для секретного ключа (необязательно, можно оставить пустым и не шифровать) + Комментарий → кнопка “Next >”: Выбираем длину ключа (в версии SecureCRT 6.1.0 максимальная длина ключа равна 2048 бит, в версии 8.5.4 — 16 384 бит): Генерирование ключа → кнопка “Next >”: Для генерирования случайных чисел нужно просит поводить мышкой в рамках окна. Сохранение пары ключей → Выбор места хранения → Выбор формата сохраняемого ключа (VanDuke Private format, OpenSSH legacy, OpenSSH new) → кнопка “Finish”: SecureCRT спрашивает, делать ли данный ключ ключом по умолчанию для SecureCRT: Выбираем параметры (тип пары: RSA; битная размерность ключа: 2048; по желанию задаём Passphrase (защита ключа с помощью пароля)) → Generate: Для гарантирования случайных чисел просит поводить мышкой в рамках окна. Это защита от псевдослучайных чисел. Сохраняем RSA-ключи → Кнопка «Save private key»: Обратите внимание: RSA-ключи, сохраненные в частном формате в одном ПО, нельзя использовать в ПО другого производителя. То есть пара RSA-ключей, созданных в PuTTYgen и сохраненных в формате Putty Private Key, не подходит для использования в SecureCRT, и наоборот. PuTTY поддерживает только формат Putty Private Key. Универсальным решением для распространения ключей является конвертирование ключей в формат OpenSSH (Смотри ссылку 2: “Conversion from Putty to SecureCRT with auth. keys”). Т. к. SecureCRT свободно работает с форматом OpenSSH. А ПО PuTTYgen преобразует формат OpenSSH в формат Putty Private Key. Чтобы использовать в SecureCRT RSA-ключи, которые сгенерированы в PuTTYgen и сохранены в формате Putty Private Key (*.ppk), экспортируем их с помощью PuTTYgen в формат OpenSSH: Чтобы использовать в PuTTY RSA-ключи, которые сгенерированы в SecureCRT и сохранены в формате VanDyke Private Key (файл публичного ключа — *.pub, файл секретного ключа *. (без расширения)), экспортируем их с помощью SecureCRT в формат OpenSSH, а затем с помощью PuTTYgen экспортируем в формат Putty Private Key (*.ppk): Будем использовать встроенную утилиту ssh-keygen (man ssh-keygen). Во время выполнения программа спросит пароль для защиты RSA-ключа: Генерируем RSA-ключ с длиной 4096 бит в с указанием имени ключа, путем к папке с местом хранения ключа, пароль задаем в явном виде в параметрах генерации ключа (-N «cisco»): Не рекомендуемые параметры генерации ключей: ненадёжный ключ длиной 1024 бита, с указанием имени ключа, путем к папке с местом хранения ключа, пароль задаем в явном виде в параметрах генерации ключа (-N «» – без пароля): Итак, мы создали три ключа в с указанием имен ключей и указанием места хранения ключей (по умолчанию все ключи сохраняются в /Users/[Username]/.ssh). По умолчанию, при подключении по SSH с аутентификацией по публичному ключу, происходит последовательный перебор всех публичных ключей, которые хранятся в папке /Users/[Username]/.ssh. Ключ R6: переименуем ключ в “id_rsa” (по умолчанию имя файла генерируемого ключа “id_rsa”) и перенесем в папку с SSH-ключами ( /.ssh/) (Т. е. выполним все действия, чтобы ключ R6 использовался как основной ключ для подключений по SSH по умолчанию): Преобразуем публичный OpenSSH-ключ в формат RFC4716 (экспорт в Cisco IOS): Как на различном оборудовании привязать открытый ключ к пользователю? Процесс привязки публичного ключа к пользователю не стандартный и меняется от оборудования к оборудованию, поэтому приведены примеры для каждого типа оборудования, которое чаще всего применяется в сети. Весь ключ вставляем в одну строчку (OpenSSH формат). Типы форматов ключей, импортируемых на Huawei: “The SecureCRT and PuTTY generate RSA keys in PEM format.” “The OpenSSH generates RSA keys in OpenSSH format.” “The OpenSSL generates RSA keys in DER format.” По умолчанию — в шестнадцатеричном виде: Примечание: оборудование Huawei поддерживает не только ключи в формате RSA, но и другие форматы: Можно жестко задать тип аутентификации для пользователя по SSH: То есть мы разрешаем доступ с помощью либо пароля, либо публичных и приватных ключей, либо и того, и другого. Конфигурация полностью аналогична настройкам на маршрутизаторе, но имеет некоторые особенности. По умолчанию уровень привилегий после журналирования с использованием сертификатов равен 0 и повышению не поддается. Поэтому уровень приоритета задается с помощью Вариант 1: предустанавливаем файл публичного ключа на устройство и привязываем файл публичного ключа к пользователю. Вариант 2: копируем публичный ключ пользователю: Этот раздел посвящен настройке SSH-клиентов для аутентификации по RSA-ключам на сетевом оборудовании (или другом оборудовании, при условии, что оборудование и ПО поддерживает аутентификацию по публичным ключам). Мы рассмотрим настройку использования публичного ключа в самых популярных программах: SecureCRT и PuTTY. В окне настроек SSH есть список Authentication. В нём необходимо увеличить приоритет PublicKey до самого высокого — сделать верхним в списке. Затем перейдите в параметры PublicKey и выберите файл приватного ключа. Самый верхний переключатель позволяет использовать глобальные настройки секретного ключа или сеансовые настройки — другой секретный ключ (ключ не по умолчанию) — только для этого подключения. Настраиваем глобальный публичный ключ: в меню Options → Global options → Категория SSH2. В настройках SSH (Connection → SSH → Auth) в поле “Private key file for authentication” укажите файл Putty Private Key (*.ppk): Настройка стандартного клиента для использования публичных ключей: Заполняется таким образом: Примечание: у меня некорректно настроено подключение по умолчанию (как правильно, я не знаю), потому что подключение к хосту R6 (10.31.73.31) выполняется очень долго. Рекомендуется указать сразу указать путь к ключу по умолчанию. Пример подключения по ssh используя публичные ключи и файл config: RSA-ключи могут использоваться для замены аутентификации по паролю, но не во всех случаях: На некотором оборудовании одному пользователю может соответствовать несколько пар публичных ключей, на другом оборудовании одному пользователю соответствует только один публичный ключ. Также разнятся форматы, в которых хранится пара из публичного и секретного ключа. Но это руководство поможет вам экспортировать ключи в разные форматы. Сегодня оптимально использовать ключи длиной 2048 бит, но для некоторого оборудования это максимально возможная длина ключа (быть может, в новых прошивках это исправят). Например: Рекомендуется использовать публичные ключи для замены паролей, если пароли вводятся с помощью скриптов (пример: autologon в SecureCRT). Рекомендуется использовать публичные ключи для защиты от передачи пароля по сети. Некоторое ПО по умолчанию использует публичные ключи для аутентификации по SSH вместо пароля (пример: Ansible).[math]\triangleleft[/math] Криптографическая стойкость [ править ]
Применение [ править ]
Шифрование [ править ]
Расшифрование [ править ]
Минусы [ править ]
Шифрование при помощи алгоритма RSA
Что представляет собой алгоритм?
Шифрование
Цифровая подпись
Скорость работы
Как взламывают алгоритм RSA?
Что собой представляют «устойчивые числа»?
Рекомендованный размер ключа
Множество простых чисел
Как это работает?
Пример работы
Иллюстрация работы RSA на примере
Шаг первый. Подготовка ключей
Шаг второй. Шифрование
Шаг третий. Расшифровка
В чём гарантия надёжности шифрования
А как это всё работает на практике?
Немного о сложностях
Аутентификация на сетевом оборудовании через SSH с помощью публичных ключей
Содержание
Введение
Restrictions for Secure Shell Version 2 Support
Rivest, Shamir, and Adleman (RSA) key generation is an SSH server-side requirement. Devices that act as SSH clients need not generate RSA keys.Создание публичного RSA-ключа
Генерирование RSA-пары в SecureCRT
Генерирование RSA-пары в PuTTYgen
Конвертирование RSA-ключа из формата Putty Private Key (PuTTY) в формат OpenSSH (SecureCRT)
Конвертирование RSA-ключа из формата VanDyke Private Key (SecureCRT) в формат Putty Private Key (PuTTY)
Генерирование публичных ключей на MAC OS X средствами операционной системы
Генерируем RSA-ключ с длиной 2048 бит с указанием имени ключа, путем к папке с местом хранения ключа:Применение публичного ключа на оборудовании
Cisco IOS XE, Catalyst (с версии 15.1 и выше), IOS
Cisco ASA
Маршрутизаторы и коммутаторы Huawei
Huawei USG (6000)
Cisco Nexus 9.3
Использование секретного ключа для подключения по SSH
SecureCRT
PuTTY
MAC OS X
Как упростить работу с SSH на MAC OS X:
Заключение