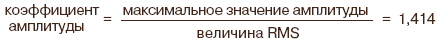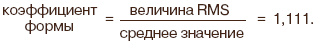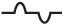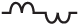rms voltage что это
Среднеквадратичное значение
Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.
Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Действующее значение напряжения и тока
В качестве примера можно рассмотреть квадратичную зависимость мощности или работы электрического тока от значений тока или напряжения.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
Величина постоянного напряжения или тока является его среднеквадратичным значением.
Среднеквадратичное значение переменного тока равно величине постоянного тока, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода.
Определяющим фактором здесь является среднее (среднеарифметическое) значение мощности P avg или работы A avg, пропорциональное квадрату значения тока.
Так же среднеквадратичное значение переменного напряжения за период равносильно по своему воздействию на активную нагрузку такому же значению постоянного напряжения.
Среднеквадратичное значение переменного напряжения или тока часто называют действующим или эффективным.
Примечание:
Электромагнитные приборы используют для измерения переменного тока и напряжения в промышленных установках. Усилие, создаваемое измерительной катушкой в электромагнитном приборе, пропорционально квадрату тока, поэтому не меняется по направлению.
Угол отклонения стрелки определится некоторым средним усилием F, которое будет пропорционально среднеквадратичному значению тока.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.
Запишем выражение U rms с применением интеграла функции U = U ampsin(t) для одного периода 2π :
Вынесем U amp из под знака радикала. Воспользуемся табличным интегралом 
Так как sin(2π), sin(4π) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:
В результате решения в итоге получим:
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T для функции 
Выразим U rms искомой функции с помощью определённого интеграла:
Используя табличный интеграл 
В итоге преобразований получим:
Для вариантов однополярного или двуполярного напряжения пилообразной и треугольной формы в периоде 2T или 4T, представленных на рисунке ниже, T и U amp имеют те же расчётные величины, что и в рассмотренном случае c функцией 

Следовательно, вышеуказанные варианты однополярного или двуполярного напряжения пилообразной и треугольной формы будут иметь среднеквадратичное значение 
В результате получаем значение RMS, равное произведению амплитуды импульсов U amp на квадратный корень из коэффициента заполнения (T i / T).
В качестве дополнительного материала предлагаем рассмотреть расчёт средеквадратичного значения напряжения накала кинескопа цветного телевизора, исходя из амплитуды и формы напряжения.
Замечания и предложения принимаются и приветствуются!
Важность использования RMS измерений для описания факторов, влияющих на качество электрической энергии

Морские волны подобны синусоидальной волне переменного напряжения, которая используется в качестве эталонной при при определении качества питания. Отклонения от чисто синусоидальной формы волны могут быть обусловлены гармоническими составляющими, некратными гармониками, а также импульсными или колебательными переходными процессами. Изменения амплитуды синусоидального сигнала можно классифицировать следующим образом: падения, всплески и продолжительное перенапряжение либо пониженное напряжение. В то время как изменения в частоте питающего напряжения сравнительно редки и возникают при серьезных неполадках оборудования, чаще имеет место сдвиг фаз при провалах и всплесках. Для того чтобы охарактеризовать или описать синусоидальный сигнал, находящийся под воздействием описанных факторов, влияющих на качество электроэнергии, используются измерения истинных среднеквадратичных значений (Root Mean Squared — RMS). Являющиеся полезными во многих ситуациях, в ряде случаев такие измерения могут оказаться неадекватными либо вводить в заблуждение.
Что же представляют собой RMS?
Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.
Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла (см. рис. 1).
Рисунок 1. Форма волны на нагрузке однофазного источника питания с полноволновым измерителем.
RMS-значение чистого синусоидального сигнала составляет примерно 70,7% пикового значения. При искаженной форме волны это не верно, что является ответом на вопрос, почему приборы, измеряющие не в терминах истинных среднеквадратичных значений, могут выдавать совершенно различные результаты при различных степенях искажений и, следовательно, не могут использоваться при наличии гармоник. Те приборы, которые лишь вычисляют 71% от пикового значения будут давать неверный результат для формы тока, показанного на рис. 1. На рисунке изображена классическая форма токового сигнала однофазного источника питания с выпрямлением полной волны, присутствующего во многих электронных устройствах. Эта форма волны с гармоническими искажениями (THD) на уровне 108% имела пиковое значение 3,6 А и истинное среднеквадратичное значение 1,4 А, что не совпадает с рассчитанной величиной 0,707×3,6=2,55 А.
Невысокого качества анализаторы электроэнергии, которые настроены на RMS-значения, могут пропускать некоторые данные. Ряд приборов рассчитывают RMS-значения в ходе нескольких циклов. Весьма вероятно, что эти мониторы не зафиксируют многофазовый провал в течение одного цикла, изображенный на рис. 2.
Рисунок 2. Провал в течение одного цикла в двух фазах.
Такое искажение сигнала типично для случая, когда неполадка устраняется с помощью защитного предохранителя. На рис. 3 провал в течение одного цикла, возникший вследствие пробоя при пиковом напряжении (возможно из-за неисправности изоляции или удара молнии) будет давать различные RMS-значения на каждом из трех циклов.
Рисунок 3. Однофазный провал при пробое пиковым напряжением.
В зависимости от механизма включения триггера и пороговых значений, возможно необнаружение провала вплоть до третьего цикла, поскольку RMS-значение неисправных циклов может превышать порог срабатывания триггера. Неисправность, выражающаяся в сдвиге фаз, может иметь идентичные значения от одного цикла к следующему, несмотря на изменения амплитуды волны. Это происходит, когда используются электроанализаторы со многими механизмами включения триггера, например при переходных процессах или искажениях формы волны. Следует помнить, что хотя прибор не замечает таких неисправностей, это не значит, что они не существуют.
Справка
Консультативно-торговая компания «Энергометрика» поставляет компоненты автоматизации для: АСУ ТП, «интеллектуальное» здание, шкаф электрический, конденсаторная установка, системы учета параметров электроэнергии. SCADA системы.
Параметры переменного напряжения
Как вы помните из предыдущей статьи, переменное напряжение — это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.
Среднее значение напряжения
Среднее значение переменного напряжения Uср — это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.
Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком «минус». А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.
То же самое касается и других сигналов, например, двухполярного меандра. Меандр — это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.
Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.
средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:
Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:
Среднеквадратичное значение напряжения
Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.
Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:
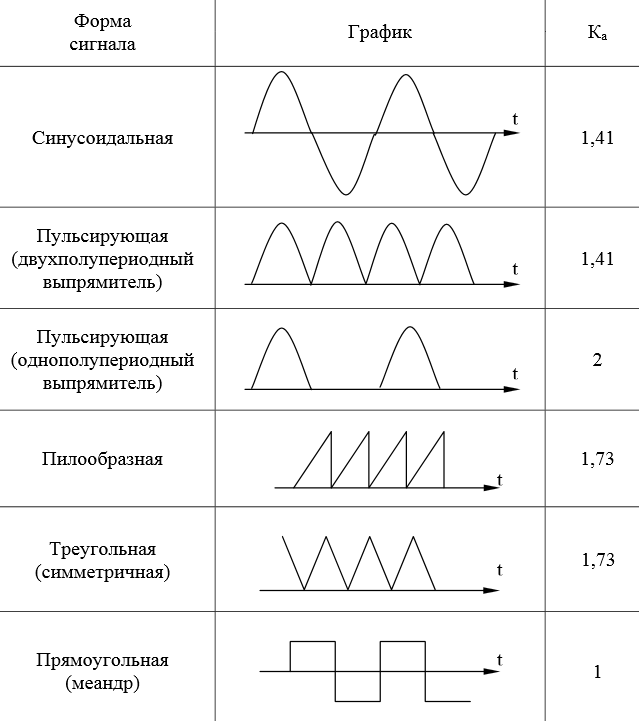
Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:
Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.
Как измерить среднеквадратичное значение напряжения
Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS — как вы уже знаете — это среднеквадратическое значение. А что за буква «T» впереди? Думаю, вы помните, как раньше была мода на одно словечко: «тру». «Она вся такая тру…», «Ты тру или не тру?» и тд. Тру (true) — с англ. правильный, верный.
Так вот, T-RMS расшифровывается как True RMS — «правильное среднеквадратическое значение». Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип «T-RMS».

Проведем небольшой опыт. Давайте соберем вот такую схемку:
Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц
генератор частоты
А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?
Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:
Итак, смотрим нашу табличку и находим интересующий нас сигнал:
Для нас не важно, пробивает ли сигнал «пол» или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды Ka= 1,73.
Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала
Проверяем нашим прибором, так ли оно на самом деле?
Супер! И в правду Тrue RMS.
Замеряем это же самое напряжение с помощью моего китайского мультиметра
Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.
Самый интересный сигнал в плане расчетов — это двуполярный меандр, ну тот есть тот, который «пробивает пол».
Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.
Вот вам небольшая картинка, чтобы не путаться
Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.
rms voltage
действующее значение напряжения
—
[Интент]
Недопустимые, нерекомендуемые
Тематики
Смотреть что такое «rms voltage» в других словарях:
Voltage regulator — A popular three pin 12 V DC voltage regulator IC. A voltage regulator is an electrical regulator designed to automatically maintain a constant voltage level. A voltage regulator may be a simple feed forward design or may include negative feedback … Wikipedia
V RMS — Voltage root mean square; average voltage equal to the maximum voltage multiplied by a constant … Dictionary of automotive terms
Orders of magnitude (voltage) — To help compare different orders of magnitude, the following list describes various voltage levels. Factor (volt) Value Item 10−7 0.5 μV Change in nerve cell potential caused by opening a single acetylcholine receptor channel[1] 10−6 2 μV Noise… … Wikipedia
True RMS converter — When measuring the value of an alternating current signal it is often necessary to convert the signal into a direct current signal of equivalent value (known as the RMS, root mean square, value). This process can be quite complex (see root mean… … Wikipedia
High-voltage direct current — HVDC or high voltage, direct current electric power transmission systems contrast with the more common alternating current systems as a means for the bulk transmission of electrical power. The modern form of HVDC transmission uses technology… … Wikipedia
Extra-low voltage — IEC voltage range AC DC defining risk High voltage (supply system) > 1000 Vrms > 1500 V electrical arcing Low voltage (supply system) 25–1000 Vrms 60–1500 V electrical shock Extra low voltage (supply system) Wikipedia
Root mean square — In mathematics, the root mean square (abbreviated RMS or rms), also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids.It… … Wikipedia
AC power — This article deals with power in AC systems. See Mains electricity for information on utility supplied AC power. Usually hidden from the unaided eye, the blinking of (non incandescent) lighting powered by AC mains is revealed in this motion… … Wikipedia
Audio power — Sound measurements Sound pressure p, SPL Particle velocity v, SVL Particle displacement ξ Sound intensity I, SIL Sound power Pac Sound power level SWL Sound energy Sound energy density … Wikipedia
Alternating current — (green curve). The horizontal axis measures time; the vertical, current or voltage. In alternating current (AC, also ac) the movement of electric charge periodically reverses direction. In direct current (DC, also dc), the flow of electric charge … Wikipedia
Истинное RМS – единственно правильное измерение
Во многих коммерческих и промышленных установках происходят постоянные отключения защитных систем. Зачастую отключения кажутся случайными и необъяснимыми, но, конечно, причина существует, а в нашем случае их две. Первая возможная причина – это противотоки, которые возникают при включении некоторых видов нагрузки, например персональных компьютеров (этот вопрос будет рассмотрен в одной из будущих публикаций данного руководства). Второй возможной причиной является то, что реальный ток, протекающий по цепи, был недоизмерен, т. е. реальные значения тока выше измеренного.






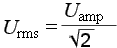
















.png)