remainder в python что это
numpy.remainder () в Python
Syntax : numpy.remainder(arr1, arr2, /, out=None, *, where=True, casting=’same_kind’, order=’K’, dtype=None, subok=True[, signature, extobj], ufunc ‘remainder’)
Parameters :
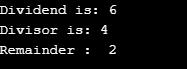
arr1 : [array_like] Dividend array.
arr2 : [array_like] Divisor array.
dtype : The type of the returned array. By default, the dtype of arr is used.
out : [ndarray, optional] A location into which the result is stored.
-> If provided, it must have a shape that the inputs broadcast to.
-> If not provided or None, a freshly-allocated array is returned.
where : [array_like, optional] Values of True indicate to calculate the ufunc at that position, values of False indicate to leave the value in the output alone.
**kwargs : Allows to pass keyword variable length of argument to a function. Used when we want to handle named argument in a function.
Код № 1:
# Программа Python, объясняющая
# numpy.remainder () функция
import numpy as geek
out_num = geek.remainder(in_num1, in_num2)
Выход :
Код № 2:
# Программа Python, объясняющая
# numpy.remainder () функция
import numpy as geek
out_arr = geek.remainder(in_arr1, in_arr2)
Какие бывают операторы в Python? Как сложить числа? А возвести в степень?
Настоящий раздел объясняет, как использовать базовые операторы в Python.
Арифметические операторы
Как и в любых других языках программирования, операторы сложения, вычитания, умножения и деления могут использоваться с числами.
Попробуйте посчитать, каким будет ответ. Соблюдает ли python порядок действий?
Другим доступным оператором является оператор по модулю (%), который возвращает целочисленный остаток от деления. делимое % делитель = остаток.
Использование двух символов умножения дает степенное соотношение.
Использование операторов со строками
Python поддерживает объединение строк с помощью оператора сложения:
Python также поддерживает умножение строк для формирования строки с повторяющейся последовательностью:
Использование операторов со списками
Списки могут объедииться с помощью операторов сложения:
Как и в строках, Python поддерживает формирование новых списков с повторяющейся последовательностью, используя оператор умножения:
Упражнение
Научим основам Python и Data Science на практике
Это не обычный теоритический курс, а онлайн-тренажер, с практикой на примерах рабочих задач, в котором вы можете учиться в любое удобное время 24/7. Вы получите реальный опыт, разрабатывая качественный код и анализируя реальные данные.
math.remainder() Function in Python with Examples
LAST UPDATED: SEPTEMBER 2, 2021
Before you think this is a simple remainder function that finds the remainder when a number is divided by the other, stop and read ahead. This isn’t what you think.
Finding the remainder when a number is divided by another is trivial. It can be done using the modulus(modulo) operator ( % ) but a modulus operator always returns a positive number(true modulus value) which makes it unsuitable if we have to use this operator with negative numbers.
Python 3.7 has introduced a new remainder method which can be found in the math library.
Syntax of remainder() method
Following is the syntax of the remainder method:
Here number_one refers to the divisor and number_two refers to the dividend.
Input:
The remainder method takes 2 inputs (they can be of integer or float type).
Output:
It returns the remainder of the division operation when the first number is divided by the second number. The return type is a floating-point value, which means it can be a fraction too.
Time for an Example!
Suppose the first number is 17 and the second number is 6.
One would expect the output to be 5. But surprisingly, with the remainder function, the output is -1.
This is because 17 can be divided by 6 twice leaving remainder aS 5, but instead of 17, if the dividend was 18, it can be completely divided by 6. This means 17 is much closer to 18 than it is to 12 (6 multiplied by 2). Hence the output would be -1 indicating that the dividend is just one number far from the number which is completely divided by the divisor.
Also, math.remainder function always fulfills the condition the below condition:
abs(reminder) math.remainder() function in action:
Output:
Special cases with the math.remainder() method
#1. When the second parameter (divisor) is an infinite value(in the math library, it can be accessed using math.inf ), and the first parameter is any finite, non-zero number, it returns the first parameter as output.
Output:
Output:
Output:
On platforms that have binary floating-point values, the result of the remainder operation is always exactly displayed, no rounding error occurs.
Conclusion:
This is a new introduction in the Python 3.7 version’s math library and is quite different than the traditional modulus operator that was used for finding remainder until now. This function expands the scope of the remainder operation.
Python Remainder Operator
By 
Introduction to Python Remainder Operator
Python remainder operators are used for the computation of some operands. Operators are special symbols that are used on operands to do some operation such as addition, subtraction, division, etc. The operators can be symbolized as ‘+’ for addition, ‘-’ for subtraction, ‘/’ for division, ‘*’ for multiplication, etc. In Python, the modulus operator is a percentage symbol (‘%’) which is also known as python remainder operator, whereas there is a division operator for integer as ’//’, which works only with integer operands also returns remainder but in integers. Similarly, the python remainder operator or modulus operator also returns the remainder when two operands are divided, i.e. one operand is divided with other operand results in us remainder. This remainder operator is used for both integers and float numbers.
Syntax:
Web development, programming languages, Software testing & others
Dividend % Divisor: The remainder is obtained when x is divided by y. The remainder will be an integer if both dividends are integers. The remainder will be a floating-point number if one among dividend or divisor is a float number.
Examples of Python Reminder Operator
Following are the different examples of Python Reminder Operator.
Example #1
Code:
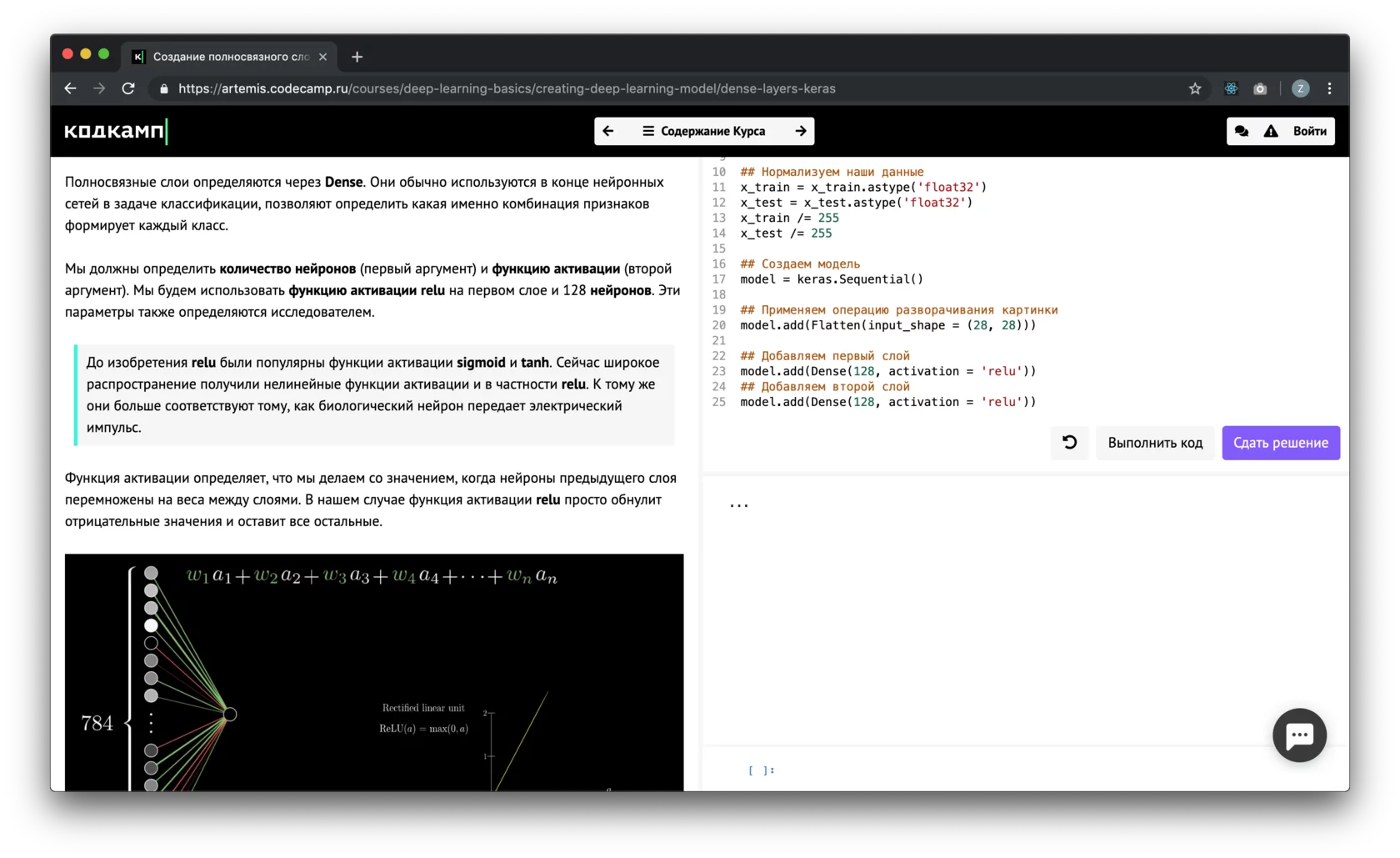
x = 5
y = 2
r = x % y
print (‘Remainder is:’, r)
Output:
Example #2
Code:
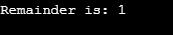
import numpy as np
n1 = 6
n2 = 4
r = np.remainder(n1, n2)
print («Dividend is:», n1)
print («Divisor is:», n2)
print («Remainder : «, r)
Output:
Explanation: The above example uses numpy.remainder() function on the given dividend and divisor to find the remains of two, which works similar to the modular operator. In this example, it is 6 % 4, 4 goes into 6, one time which yields 4 so the remainder is 6 – 4 =2.
Example #3
Code:
Output:
Example #4
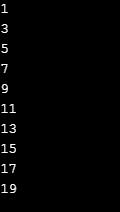
A remainder operator or modulo operator is used to find even or odd numbers. Below is a piece of code to print odd numbers between 0 and 20.
Code:
Output:
Explanation: In the above example using a modulo operator, it prints odd numbers between 0 and 20 from the code; if the number is divided by 2 and the remainder obtained is 0, then we say it as an even number; else its odd number. If the number is 2, then 2 % 2 gives remainder 0, so its an even number, not odd, now; if the number is 3, then 3 % 2 gives remainder 1, which 2 goes into 3 one time so yields 2 and remainder is 3 – 2 =1 which not zero so the given number 3 is odd and using for loop it will check till 20 numbers and print all the odd numbers between 0 and 20. Modulo operator or Remainder operator is also used on floating-point numbers, not like division operator ( // ), which is used only on integers and gives remainder also in integer form.
Example #5
Code:
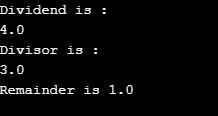
a = input(«Dividend is :\n»)
fa = float(a)
b = input(«Divisor is :\n»)
fb = float(b)
fr = fa % fb
print («Remainder is»,fr)
Output:
Example #6
In Python, the modulo operator can be used on negative numbers also which gives the same remainder as with positive numbers, but the negative sign of the divisor will be the same in the remainder.
Code:
Output:
Code:
Output:
Logic Behind the Code:
Explanation: These negative numbers use the fmod() function to find the remainder; if any one of the numbers among dividend or divisor is negative, then we can even use the fmod() function of the math library, and this can also be used to find the remainder of floating-point numbers also.
Example #7
Code:
Output:
Explanation: In Python, the modulo operator gives an error when the divisor is zero (0). Usually, it gives ZeroDivisionError as we know any number divided by zero is infinity (∞).
Example #8
Code:
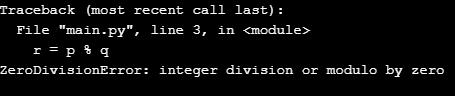
p = 10
q = 0
r = p % q
print(r)
The above code gives us an error, as shown in the below screenshot.
Output:
Code:
p = 10
q = 0
try:
rem = p * q
print(rem)
except ZeroDivisionError as zde:
print(«Cannot divided by 0»)
This error can be caught by using try-except blocks, as shown in the below screenshot.
Output:
Conclusion
Recommended Articles
This is a guide to Python Reminder Operator. Here we discuss the Introduction to Python Reminder Operator along with examples and code implementation. You may also have a look at the following articles to learn more –
Python Training Program (36 Courses, 13+ Projects)
Python math.remainder() Method
Example
Return the remainder of x with respect to y:
# Import math Library
import math
# Return the remainder of x/y
print (math.remainder(9, 2))
print (math.remainder(9, 3))
print (math.remainder(18, 4))
Definition and Usage
The math.remainder() method returns the remainder of x with respect to y.
Syntax
Parameter Values
| Parameter | Description |
|---|---|
| x | Required. The number you want to divide. |
| y | Required. The number you want to divide with. It must be a non-zero number, or a ValueError occurs. |
Technical Details
| Return Value: | A float value, representing the remainder |
|---|---|
| Python Version: | 3.7 |
More Examples
Example
Return the remainder of x/y:
We just launched
W3Schools videos
COLOR PICKER
Get certified
by completing
a course today!
CODE GAME
Report Error
If you want to report an error, or if you want to make a suggestion, do not hesitate to send us an e-mail:
Thank You For Helping Us!
Your message has been sent to W3Schools.
Top Tutorials
Top References
Top Examples
Web Courses
W3Schools is optimized for learning and training. Examples might be simplified to improve reading and learning. Tutorials, references, and examples are constantly reviewed to avoid errors, but we cannot warrant full correctness of all content. While using W3Schools, you agree to have read and accepted our terms of use, cookie and privacy policy.