r2bc что это такое

Реактивное программирование со Spring, часть 4 R2DBC

Это четвертая часть серии заметок о реактивном программировании, в которой будет представлено введение в R2DBC и описано, как мы можем использовать Spring Data R2DBC для создания полностью реактивного приложения.

1. Что такое R2DBC?

Если вы еще не знакомы с реактивным программированием и реактивными потоками, я рекомендую вам сначала прочитать введение в реактивное программирование, в котором описывается мотивация, лежащая в основе этой парадигмы программирования.

При разработке реактивного приложения, которое должно включать доступ к реляционной базе данных, JDBC не подходит, поскольку это блокирующий API.

На данный момент существуют реализации драйверов для Oracle, Microsoft SQL Server, MySQL, PostgreSQL, H2, MariaDB и Google Cloud Spanner.

2. SPRING DATA R2DBC

Чтобы продемонстрировать, как его можно использовать, давайте вернемся к примеру StudentController из предыдущей заметки о WebFlux:

Этот контроллер содержит несколько различных методов для выполнения действий над учащимися. Мы видим, что он использует StudentService для выполнения этих действий. Теперь мы рассмотрим эту функциональность, лежащую в основе контроллера REST, и то, как мы можем реализовать доступ к базе данных с помощью R2DBC.

2.1 Пример реализации

2.1.1 Зависимости

Во-первых, нам нужно добавить в наш проект пару новых зависимостей:

Нам нужно включить spring-boot-starter-data-r2dbc, чтобы включить spring-data-r2dbc. В этом примере мы будем использовать базу данных postgresql, поэтому нам нужно добавить r2dbc-postgresql, чтобы получить необходимую реализацию драйвера r2dbc.

2.1.2 Конфигурация базы данных

Мы можем либо добавить детали подключения к нашей базе данных в application.properties:

или используйте конфигурацию на основе Java:

2.1.3 STUDENTSERVICE

Теперь давайте посмотрим на StudentService, который использует StudentController:

Как видите, он использует StudentRepository для выполнения различных операций с базой данных над учащимися. Итак, теперь давайте взглянем на этот репозиторий.

2.1.4 STUDENTREPOSITORY

Более сложные запросы также можно определить, добавив аннотацию @Query к методу и указав фактический sql.

Помимо ReactiveCrudRepository, существует также расширение ReactiveSortingRepository, которое предоставляет дополнительные методы для извлечения отсортированных сущностей.

2.1.5 STUDENT

Наконец, давайте посмотрим на реализацию Student:

Идентификатор объекта должен быть аннотирован аннотацией Spring Data @Id.

Аннотации @Table не обязательны, но ее добавление позволяет сканеру пути к классам находить и предварительно обрабатывать объекты для извлечения связанных метаданных. Если вы не добавите его, это произойдет при первом сохранении объекта, что может немного отрицательно повлиять на производительность.

Lombok рекомендуется использовать, чтобы избежать шаблонного кода.

Есть также некоторые другие рекомендации для обеспечения оптимальной производительности, вы можете найти подробности в справочной документации.

2.1.6 Другие варианты запросов

Вместо использования репозитория вы можете выполнить инструкцию SQL напрямую, используя DatabaseClient.

Например, чтобы получить всех студентов:

Также можно использовать R2dbcEntityTemplate для выполнения операций с сущностями. Например:

2.2 Другие особенности

2.2.1 Оптимистическая блокировка

2.2.2 Транзакции

Spring поддерживает управление реактивными транзакциями через SPI ReactiveTransactionManager. Аннотации @Transactional можно наносить на реактивных методах возвращающихся типов Publisher и программное управление транзакциями может быть применено с использованием TransactionalOperator.

2.2.3 Реактивные библиотеки

Как и WebFlux, Spring Data R2DBC требует Project Reactor в качестве основной зависимости, но он совместим с другими реактивными библиотеками, реализующими спецификацию Reactive Streams. Репозитории существуют также для RxJava2 и RxJava3 (см. обзор пакета).

2.2.4 Пул соединений

Для пула соединений доступна библиотека под названием r2dbc-pool. Подробнее о том, как его использовать, читайте здесь.

3. Готовность для продакшн

Спецификация R2DBC: 0.8.5

Spring Data R2DBC: 1.3.1

Прежде чем принять решение об их использовании для вашего приложения, конечно, рекомендуется более внимательно изучить текущее состояние драйвера базы данных и реализаций пула в соответствии с вашими требованиями. Есть некоторые нерешенные проблемы, которые могут помешать вам сделать этот шаг на данный момент, но улучшения продолжаются.

4. Подводя итог…

Это сообщение в блоге продемонстрировало, как Spring Data R2DBC можно использовать в приложении WebFlux. Таким образом, мы создали полностью реактивное приложение и подошли к концу этой серии статей о реактивном программировании.

Как вы, возможно, помните из первого сообщения в блоге, ключевыми факторами, лежащими в основе модели реактивного программирования, являются следующие:

отход от потока на модель запроса и может обрабатывать больше запросов с небольшим количеством потоков

предотвращение блокировки потоков при ожидании завершения операций ввода-вывода

упрощение параллельных вызовов

поддержка «обратного давления», давая клиенту возможность сообщить серверу, с какой нагрузкой он может справиться

Еще не решено, когда изменения будут внесены в официальный выпуск Java, но двоичные файлы раннего доступа доступны для загрузки.

Источник

Знакомство с P2P-трейдингом: что это такое и как функционирует локальная ВТС-биржа

Опытные пользователи и обладатели виртуальной валюты все чаще и чаще склоняются к такому виду купли-продажи коинов, как peer-to-peer. Были разработаны специальные площадки, которые позволяют клиентам сети без участия посредников заключать сделки и не переживать за свои финансы. Для того чтобы довериться Р2Р-торговле, необходимо оценить все «за» и «против», а также понять особенности работы системы.

Особенности peer-to-peer трейдинга

Часто из уст пользователей сети блокчейн и держателей виртуадьных валют можно услышать такое словосочетание как «peer-to-peer торговля». Это возможность напрямую покупать виртуальную валюту или продавать ее другому пользователю сети.

В данном процессе не принимают участие сторонние люди, а также органы власти, посредники и так далее. Взаимодействие осуществляется в сети напрямую. Это тотальная свобода, независимость и право выбора для каждого человека. Здесь можно анализировать представленные графики, рыночные инструменты, фильтровать участников системы по активности и успешности, для того чтобы приходить к выводу: с кем можно сотрудничать, а с кем — не стоит, когда лучше хранить виртуальную валюту, а когда — продавать. Криптобиржа организовывает перевод средств от имени пользователя, а рыночная цена определяет окончательную цену в момент перевода средств.

P2P-торговля – это возможность не зависеть ни от кого, отвечать за свои поступки самостоятельно, анализировать актуальные рыночные предложения, оказывать воздействие на образование цен, контролировать сделки. Иначе говоря, человек самостоятельно держит руку на пульсе жизни криптопространства и оказывает влияние на его динамику. Одной из таких популярных платформ является Бинанс Р2Р, которая гарантирует повышенный уровень безопасности каждому клиенту и создает все условия для комфортной торговли с максимальной защитой.

Особенности функционирования Р2Р-бирж

Некоторые люди ассоциируют peer-to-peer платформы с различными маркетплейсами, к примеру, Craigslist или маркетплейс от Фейсбук. Тут действительно имеется что-то общее.

Так как два пользователя сети являются непосредственными участниками сделки и больше никто. Каждый имеет право просматривать размещенные варианты объявлений, проводить мониторинг предложений, сопоставлять выгодные варианты, заключать сделки, продавать товар и предоставлять услуги. Такой же подход и у peer-to-peer бирж. Главное их преимущество заключается в повышенном уровне защиты, предоставляемом каждому человеку при переводе средств и покупке виртуальной валюты.

Некоторые относят и Твиттер к peer-to-peer платформе, но это ошибочное мнение, так как в данном контексте бессмысленно говорить о доверии. Если взаимодействовать через сторонние сервисы, а не Р2Р платформы есть риск того, что недобросовестный человек, находящийся по ту сторону экрана, попросту не переведет виртуальную валюту, если это продавец, или же не отправит деньги, если речь идет о покупателе. Поэтому здесь все происходит на страх и риск двух участников сделки. В то время как риск мошенничества при реализации Р2Р-сделок на криптобирже сведен к нулю.

Платформа Бинанс Р2Р старается предоставить консультации, защиту, поддержку и высокий уровень безопасности как покупателю, так и продавцу. Кроме этого, компания дорожит своей репутацией, и не может рисковать статусом в глазах потенциальных и реальных потребителей. Площадкой Бинанс применяется эскроу-сервис, который помогает защитить виртуальную валюту и сохранить ее в безопасном месте до того момента, как обе стороны сделки подтвердят транзакцию. К примеру, человек покупает Биткоин за фиатные деньги. Продавец отправляет ВТС в эскроу-сервис Бинанс. По факту того, как будет отправлен фиат и получено подтверждение со стороны продавца, Бинанс автоматически зачислит ВТС.

Основные «за» P2P-криптобиржи

К основным преимуществам P2P можно отнести следующие:

Минусы P2P-криптобиржи

К недостаткам P2P можно отнести:

Как защититься от аферистов и недоброжелателей на P2P

Первым делом стоит определиться с надежной биржей, например, отдать свое предпочтение Бинанс. Так как платформы подобного рода обладают высокими позициями в рейтингах, гарантируют повышенную безопасность и другие плюшки. Отталкиваться также стоит от отзывов реальных пользователей, которые оставляют свои комментарии в сети интернет на разных форумах.

Интересно, что торговля на Бинанс Р2Р способна приносить действительно высокий заработок. Так как цену формируют сами участники сообщества. У каждого есть своя свобода выбора в плане метода оплаты, установки цены и так далее. Наличие специальных фильтров поможет отсеять объявления в соответствии с предпочтениями пользователя.

Основное преимущество Р2Р криптобирж по типу Бинанс заключается в том, что на сайтах публикуются графики, обзоры и новости. То есть, достаточно понять базовые концепции, узнать, что такое доход, убытки, спрос и предложение. К примеру, если человек купил ВТС за 39 900, а продал за 40 100, то размер его прибыли будет 200 долларов. Математика проста. И инструкции, подсказки, советы на сайте смогут в этом помочь.

Есть возможность заработка и во время падения рынка. Так как можно хранить криптоактивы, находясь в активном ожидании фазы роста. Даже можно получать пассивный доход, если применять в своей работе продукты Binance Savings и получать по ним проценты. Binance Savings — это депозиты с плавающей и фиксированной ставкой для ВТС и других альткоинов с привлекательной доходностью.

Как увеличить количество сделок на Бинанс Р2Р

Каждого трейдера интересует данный вопрос. Здесь имеется несколько рекомендаций от экспертов:

Это фундаментальные аспекты P2P-торговли на Бинанс. Торговцы из разных уголков земного шара активно используют Binance P2P, чтобы получать заработок, торгуя популярными цифровыми валютами, в числе которых внутрисистемная монета платформы BNB, Биткоин (BTC), Ethereum (ETH), а также стейблкоины: Tether (USDT), Бинанс USD (BUSD) и другие коины.

Источник

2 Пи р квадрат это формула

Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:

S=πr 2 – это произведение числа пи на квадрат радиуса.

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности .

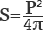
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.

Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.

Перевод радиан в градусы.
A_d = A_r * 180 / пи
Где A_d — угол в градусах, A_r — угол в радианах.

Перевод градусов в радианы.
A_r = A_d * пи / 180
Где A_d — угол в градусах, A_r — угол в радианах.

Длина окружности.
L = 2 * пи * R
Где L — длина окружности, R — радиус окружности.

Длина дуги окружности.
L = A * R
Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах
Для окружности A = 2*пи (360 градусов), получим L = 2*пи*R.

Площадь треугольника.
S = (p * (p-a) * (p-b) * (p-c) ) 1/2
Где S — площадь треугольника, a, b, c — длины сторон,
p=(a+b+c)/2 — полупериметр.

Площадь круга.
S = пи * R 2
Где S — площадь круга, R — радиус круга.

Площадь сектора.
S = L_d * R/2 = (A * R 2 )/2
Где S — площадь сектора, R — радиус круга, L_d — длина дуги.

Площадь поверхности шара.
S = 4 * пи * R 2
Где S — площадь поверхности шара, R — радиус шара.

Площадь боковой поверхности цилиндра.
S = 2 * пи * R * H
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь полной поверхности цилиндра.
S = 2 * пи * R * H + 2 * пи * R 2
Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Площадь боковой поверхности конуса.
S = пи * R * L
Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Площадь полной поверхности конуса.
S = пи * R * L + пи * R 2
Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса.

Объем шара.
V = 4 / 3 * пи * R 3
Где V — объем шара, R — радиус шара.

Объем цилиндра.
V = пи * R 2 * H
Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра.

Объем конуса.
V = пи * R * L = пи * R * H/cos (A/2) = пи * R * R/sin (A/2)
Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса.

Содержание

История [ править | править код ]

Использование многоугольников [ править | править код ]

Площадь правильного многоугольника равна половине периметра, умноженного на апофему (высоту). При увеличении числа сторон многоугольник стремится к окружности, а апофема стремится к радиусу. Это даёт основание считать, что площадь круга равна произведению половины длины окружности на радиус. [3]

Доказательство Архимеда [ править | править код ]

Следуя Архимеду, сравним площадь круга с площадью прямоугольного треугольника, основание которого равно длине окружности, а высота равна радиусу. Если площадь круга не равна площади треугольника, она должна быть меньше или больше. Исключим оба варианта, что оставит только одну возможность — площади равны. Для доказательства будем использовать правильные многоугольники.

Не больше [ править | править код ]

Предположим, что площадь круга C больше площади треугольника T = 1 ⁄₂cr. Пусть E означает превышение площади. Впишем [en] квадрат в окружность, чтобы все его четыре угла лежали на окружности. Между квадратом и окружностью четыре сегмента. Если общая их площадь G₄ больше E, делим каждую дугу пополам, что превращает вписанный квадрат в восьмиугольник и образует восемь сегментов с меньшим общим зазором, G₈. Продолжаем деление, пока общий зазор G_n не станет меньше E. Теперь площадь вписанного многоугольника P_n = C − G_n должна быть больше площади треугольника.

G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>>»> E = C − T > G n P n = C − G n > C − E P n > T E&<>=C-T\&<>>G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>> G_ \P_ &<>=C-G_ \&<>>C-E\P_ &<>>Tend>»/>

Но это ведёт к противоречию. Для доказательства проведём высоту из центра окружности на середину стороны многоугольника, её длина h меньше радиуса окружности. Пусть каждая сторона многоугольника имеет длину s, сумма всех сторон составит ns, и эта величина меньше длины окружности. Площадь многоугольника состоит из n равных треугольников высоты h с основанием s, что даёт 1 ⁄₂nhs. Но h 1 ⁄₂cr, получили противоречие.

Не меньше [ править | править код ]

Предположим, что площадь круга меньше площади треугольника. Пусть D означает разницу площадей. Описываем квадрат вокруг окружности, так что середины сторон лежат на ней. Если суммарный зазор между квадратом и окружностью G₄ больше D, срезаем углы касательными, превращая квадрат в восьмиугольник и продолжаем такие отсечения пока площадь зазора не станет меньше D. Площадь многоугольника P_n должна быть меньше T.

G_ \P_ &<>=C+G_ \&<> D = T − C > G n P n = C + G n C + D P n T =T-C\&<>>G_ \P_ &<>=C+G_ \&<> G_ \P_ &<>=C+G_ \&<>

Это тоже приводит к противоречию. Каждый перпендикуляр, проведённый от центра круга к середине стороны, является радиусом, т.е. имеет длину r. А поскольку сумма сторон больше длины окружности, многоугольник из n одинаковых треугольников даст площадь, большую T. Снова получили противоречие.

Таким образом, площадь круга в точности равна площади треугольника.

Доказательство перегруппировкой [ править | править код ]

многоугольник			параллелограмм
n	сторона	основание	высота	площадь
4	1,4142136	2,8284271	0,7071068	2,0000000
6	1,0000000	3,0000000	0,8660254	2,5980762
8	0,7653669	3,0614675	0,9238795	2,8284271
10	0,6180340	3,0901699	0,9510565	2,9389263
12	0,5176381	3,1058285	0,9659258	3,0000000
14	0,4450419	3,1152931	0,9749279	3,0371862
16	0,3901806	3,1214452	0,9807853	3,0614675
96	0,0654382	3,1410320	0,9994646	3,1393502
∞	1/∞	π	1	π

Интегрирование [ править | править код ]

Используя интегралы, мы можем просуммировать площадь круга, разделив его на концентрические окружности подобно луковице. Площадь бесконечно тонкого «слоя» радиуса t будет равна 2 π t dt, то есть произведению длины окружности на толщину слоя. В результате получим элементарный интеграл для круга радиуса r.

Можно разбивать круг не на кольца, а на треугольники с бесконечно малым основанием. Площадь каждого такого треугольника равна 1/2 * r * dt. Суммируя (интегрируя) все площади этих треугольников, получим формулу круга:

Быстрая аппроксимация [ править | править код ]

Метод удвоения Архимеда [ править | править код ]

Если задан круг, пусть u_n будет периметром вписанного правильного n-угольника, а U_n — периметром описанного правильного n-угольника. Тогда u_n и U_n являются нижней и верхней границей длины окружности, которые становятся точнее с ростом n, а их среднее значение (u_n + U_n)/2 становится особенно хорошей аппроксимацией длины окружности. Чтобы вычислить u_n и U_n для больших n, Архимед вывел следующие формулы:

u 2 n = U 2 n u n = u_ >>> (среднее геометрическое) U 2 n = 2 U n u n U n + u n = u_ > +u_ >>> (среднее гармоническое).

Начав с шестиугольника, Архимед удваивал n четыре раза, дойдя до 96-угольника, который дал ему хорошую аппроксимацию длины окружности круга.

В современных обозначениях можно воспроизвести эти вычисления (и пойти дальше). Для единичной окружности вписанный шестиугольник имеет периметр u₆ = 6, а описанный шестиугольник имеет периметр U₆ = 4√3. Удваиваем семь раз, получаем

knu_nU_n(u_n + U_n)/466,00000006,92820323,23205081126,21165716,43078063,16060942246,26525726,31931993,14614433486,27870046,29217243,14271824966,28206396,28542923,141873351926,28290496,28374613,141662863846,28311526,28332553,141610277686,28316786,28322043,1415970

Улучшение Снелла-Гюйгенса [ править | править код ]

Снелл предложил (а Гюйгенс доказал) более тесные границы, чем у Архимеда:

Для n = 48 формула даёт приближение лучше (около 3,14159292), чем метод Архимеда для n = 768.

Развитие формулы удваивания Архимеда [ править | править код ]

В первом равенстве отрезок C′P равен сумме C′O+OP, что равно r+ 1 ⁄₂c_n, а отрезок C′C является диаметром и его длина равна 2r. Для единичного круга получаем знаменитую формулу удвоения Людольфа Ван Цейлена

Если мы теперь построим правильный описанный n-угольник со стороной ″B″, параллельной AB, то OAB и OA″B″ являются подобными с отношением подобия A″B″ : AB = OC : OP. Обозначим описанную сторону S_n, тогда отношение превращается в S_n : s_n = 1 : 1 ⁄₂c_n. (Мы снова используем факт, что OP равен половине A′B.) Получаем

Обозначим периметр вписанного многоугольника через u_n = ns_n, а описанного через U_n = nS_n. Комбинируя равенства, получим

Можно также вывести

Аппроксимация случайными бросаниями [ править | править код ]

Конечная перегруппировка [ править | править код ]

Обобщения [ править | править код ]

Мы можем растянуть круг до формы эллипса. Поскольку это растяжение является линейным преобразованием плокости, оно изменяет площадь, но сохраняет отношения площадей. Этот факт можно использовать для вычисления площади произвольного эллипса, отталкиваясь от площади круга.

Пусть единичный эллипс описан квадратом со стороной 2. Преобразование переводит круг в эллипс путём сжатия или растяжения горизонтального и вертикального диаметров до малой и большой оси эллипса. Квадрат становится прямоугольником, описанным вокруг эллипса. Отношение площади круга к площади квадрата равно π /4, и отношение площади эллипса к площади прямоугольника будет тоже π /4. Если a и b — длины малой и большой осей эллипса. Площадь прямоугольника будет равна ab, а тогда площадь эллипса — π ab/4.

Мы можем распространить аналогичные техники и на большие размерности. Например, если мы хотим вычислить объём внутри сферы, и мы знаем формулу для площади сферы, мы можем использовать приём, аналогичный «луковичному» подходу для круга.

Источник