примеры симметрии в жизни
10 превосходных примеров симметрии в природе
На протяжении веков симметрия остается предметом, который очаровывает философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были совершенно одержимы ею – и даже сегодня мы, как правило, сталкиваемся с симметрией во всем от расположения мебели до стрижки волос.
Просто имейте в виду: как только вы осознаете это, вы, вероятно, испытаете непреодолимое желание искать симметрию во всем, что видите.
Возможно увидев брокколи романеско в магазине, вы подумали, что это ещё один образец генномодифицированного продукта. Но на самом деле это ещё один пример фрактальной симметрии природы. Каждое соцветие брокколи имеет рисунок логарифмической спирали. Романеско внешне похожа на брокколи, а по вкусу и консистенции – на цветную капусту. Она богата каротиноидами, а также витаминами С и К, что делает её не только красивой, но и здоровой пищей.
На протяжении тысяч лет люди удивлялись идеальной гексагональной форме сот и спрашивали себя, как пчелы могут инстинктивно создать форму, которую люди могут воспроизвести только с помощью циркуля и линейки. Как и почему пчелы имеют страстное желание создавать шестиугольники? Математики считают, что это идеальная форма, которая позволяет им хранить максимально возможное количество меда, используя минимальное количество воска. В любом случае, все это продукт природы, и это чертовски впечатляет.
Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии, известной как последовательность Фибоначчи. Последовательность Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел). Если бы мы не спешили и подсчитали количество семян в подсолнухе, то мы бы обнаружили, что количество спиралей растет по принципам последовательности Фибоначчи. В природе есть очень много растений (в том числе и брокколи романеско), лепестки, семена и листья которых отвечают этой последовательности, поэтому так трудно найти клевер с четырьмя листочками.
Но почему подсолнечник и другие растения соблюдают математические правила? Как и шестиугольники в улье, все это – вопрос эффективности.
Помимо растений, некоторые животные, например Наутилус, отвечают последовательности Фибоначчи. Раковина Наутилуса закручивается в «спираль Фибоначчи». Раковина пытается поддерживать одну и ту же пропорциональную форму, что позволяет ей сохранять её на протяжении всей жизни (в отличие от людей, которые меняют пропорции на протяжении жизни). Не все Наутилусы имеют раковину, выстроенную по правилам Фибоначчи, но все они отвечают логарифмической спирали.
Прежде, чем вы позавидуете моллюскам-математикам, вспомните, что они не делают этого специально, просто такая форма наиболее рациональна для них.
Большинство животных имеют двустороннюю симметрию, что означает, что они могут быть разделены на две одинаковых половинки. Даже люди обладают двусторонней симметрией, и некоторые ученые полагают, что симметрия человека является наиболее важным фактором, который влияет на восприятие нашей красоты. Другими словами, если у вас однобокое лицо, то остается надеяться, что это компенсируется другими хорошими качествами.
Некоторые доходят до полной симметрии в стремлении привлечь партнера, например павлин. Дарвин был положительно раздражен этой птицей, и написал в письме, что «Вид перьев в хвосте павлина, всякий раз, когда я смотрю на него, делает меня больным!» Дарвину, хвост казался обременительным и не имеющим эволюционного смысла, так как он не соответствовал его теории «выживания наиболее приспособленных». Он был в ярости, пока не придумал теорию полового отбора, которая утверждает, что животные развивают определенные функции, чтобы увеличить свои шансы на спаривание. Поэтому павлины имеют различные приспособления для привлечения партнерши.
Есть около 5000 типов пауков, и все они создают почти идеальное круговое полотно с радиальными поддерживающими нитями почти на равном расстоянии и спиральной тканью для ловли добычи. Ученые не уверены, почему пауки так любят геометрию, так как испытания показали, что круглое полотно не заманит еду лучше, чем полотно неправильной формы. Ученые предполагают, что радиальная симметрия равномерно распределяет силу удара, когда жертва попадает в сети, в результате чего получается меньше разрывов.
Дайте паре обманщиков доску, косилки и спасительную темноту, и вы увидите, что люди тоже создают симметричные формы. Из-за того, что круги на полях отличаются сложностью дизайна и невероятной симметрией, даже после того, как создатели кругов признались и продемонстрировали свое мастерство, многие люди до сих пор верят, что это сделали космические пришельцы.
По мере усложнения кругов все больше проясняется их искусственное происхождение. Нелогично предполагать, что пришельцы будут делать свои сообщения все более трудными, когда мы не смогли расшифровать даже первые из них.
Независимо от того, как они появились, круги на полях приятно рассматривать, главным образом потому, что их геометрия впечатляет.
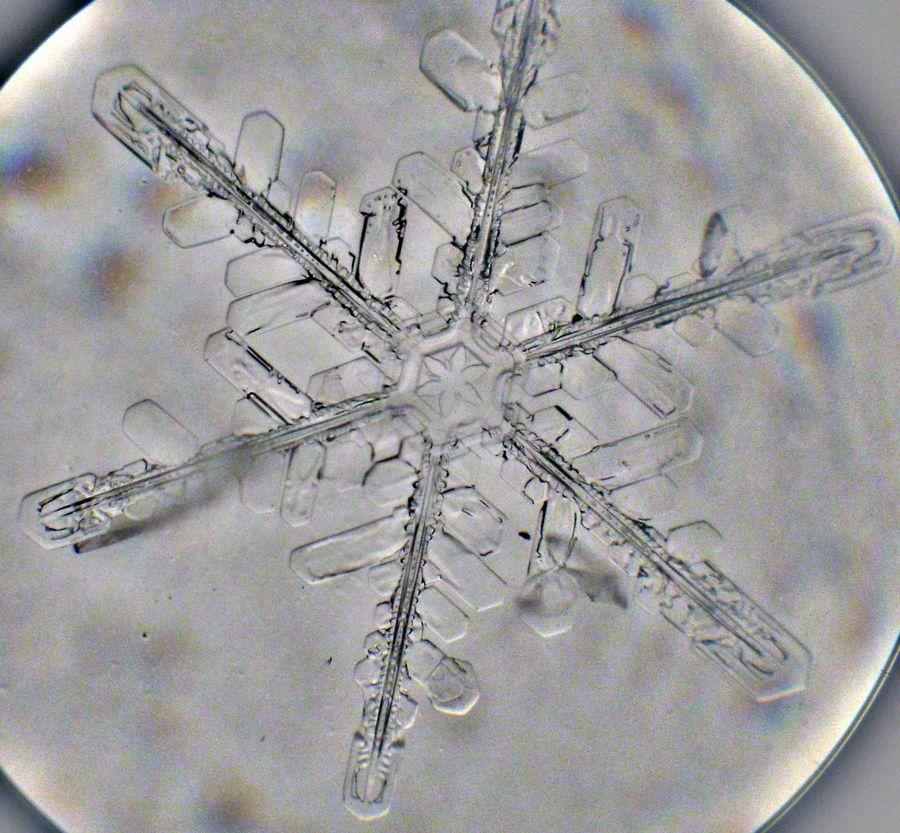
Даже такие крошечные образования, как снежинки, регулируются законами симметрии, так как большинство снежинок имеет шестигранную симметрию. Это происходит в частности из-за того, как молекулы воды выстраиваются, когда затвердевают (кристаллизуются). Молекулы воды приобретают твердое состояние, образуя слабые водородные связи, они выравниваются в упорядоченном расположении, которое уравновешивает силы притяжения и отталкивания, формируя гексагональную форму снежинки. Но при этом каждая снежинка симметрична, но ни одна снежинка не похожа на другую. Это происходит потому, что падая с неба, каждая снежинка испытывает уникальные атмосферные условия, которые заставляют её кристаллы располагаться определенным образом.
Галактика Млечный Путь
Как мы уже видели, симметрия и математические модели существуют почти везде, но разве эти законы природы ограничиваются нашей планетой? Очевидно, нет. Недавно открыли новую секцию на краю Галактики Млечного Пути, и астрономы считают, что галактика представляет собой почти идеальное зеркальное отражение себя.
Если учесть, что Солнце имеет диаметр 1,4 млн. км, а Луна – 3474 км, кажется почти невозможным то, что Луна может блокировать солнечный свет и обеспечивать нам около пяти солнечных затмений каждые два года. Как это получается? Так совпало, что наряду с тем, что ширина Солнца примерно в 400 раз больше, чем Луна, Солнце также в 400 раз дальше. Симметрия обеспечивает то, что Солнце и Луна получаются одного размера, если смотреть с Земли, и поэтому Луна может закрыть Солнце. Конечно, расстояние от Земли до Солнца может увеличиваться, поэтому иногда мы видим кольцевые и неполные затмения. Но каждые один-два года происходит точное выравнивание, и мы становимся свидетелями захватывающих событий, известных как полное солнечное затмение. Астрономы не знают, как часто встречается такая симметрия среди других планет, но они думают, что это довольно редкое явление. Тем не менее, мы не должны предполагать, что мы особенные, так как все это дело случая. Например, каждый год Луна отдаляется примерно на 4 см от Земли, это означает, что миллиарды лет назад каждое солнечное затмение было бы полным затмением. Если и дальше все пойдет так, то полные затмения, в конце концов, исчезнут, и это будет сопровождаться исчезновением кольцевых затмений. Получается, что мы просто находимся в нужном месте в нужное время, чтобы увидеть это явление.
А вы знали, что у нас есть Instagram и Telegram?
Подписывайтесь, если вы ценитель красивых фото и интересных историй!
Примеры симметрии в жизни
1.1. Что такое симметрия. 4
1.4. Симметрия в русском языке..………………………………..……………8
1.5. Симметрия в окружающем мире………………………..…….………….9
Список использованных источников………………………………………………..17
На уроках математики мы изучали симметрию, но оказалось, что на эту тему отводится мало времени. И мне захотелось узнать по больше о симметрии.
В работе мы рассмотрим понятие «симметрия» шире, не ограничиваясь рамками математики. Окружающий нас мир во многом симметричный — симметрией обладают насекомые и звери, цветы и деревья, предметы быта и архитектурные сооружения.
Изучение понятия «симметрия»;
Какую роль играет симметричность;
Симметрия вокруг нас.
Доказать, почему важна симметрия;
Рассмотреть виды симметрии, и где встречается;
Провести эксперимент и выяснить, симметрично ли лицо человека;
Объектом исследования является симметрия, а предметом – симметрия в природе и окружающем мире.
При проведении работы были использованы методы наблюдения, анкетирование, эксперимент и теоретический анализ.
1.1.Что такое симметрия?
Чтобы выяснить, что знают ребята начальной школы, мы провели опрос что такое симметрия и где она встречается. В нем приняло участие 90 человек.
Из анкетирования мы узнали, что учащиеся мало знают где встречается симметрия и что это такое.
У нас получились следующие результаты:
На первый вопрос знают правильный ответ только 9 человек. На второй
Прочитав энциклопедии и учебники, я узнал, что самые совершенные формы создает природа, и именно она придает этим формам необыкновенно гармоничные цветовые сочетания (бабочка, оса, стрекоза). Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта. Я обратил внимание на то, как строги симметричные формы античных зданий, гармоничны древнегреческие вазы, соразмерны их орнаменты. С тем или иными проявлениями симметрии мы встречаемся буквально на каждом шагу.
Так что же такое симметрия? Мы посмотрели в нескольких источниках. В толковом словаре С.И. Ожегова:
В толковом словаре В.И. Даля:
В Большой Советской энциклопедии:
Симметрия – это свойство геометрической фигуры, характеризующее некоторую правильность формы, неизменность её при действии движений и отражений.
Из найденных определений наиболее понятным для меня явилось определение данное C.И. Ожиговым. Определения разные, но во всех встречается слово соразмерность.
Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, но и уникальное средство познания красоты. В математике рассматриваются различные виды симметрии. Каждая из них имеет своё название.
В природе наиболее распространены следующие виды симметрии – «зеркальная», осевая, центральная симметрии.
«Зеркальной» симметрией обладает бабочка, листок или жук и часто такой вид симметрии называется «симметрией листка». К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.
Я посмотрелся в зеркало и задумался о том, что моя левая рука в зеркале является правой и наоборот.
Я узнал, что в школьном курсе геометрии рассматриваются три вида симметрии: симметрия относительно точки (центральная симметрия); симметрия относительно прямой (осевая или зеркальная симметрия); симметрия относительно плоскости. Центральная симметрия.Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1. Точка О считается симметричной самой себе.
Осевая симметрия. Преобразование фигуры F в фигуру F1, при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии.
Для того, чтобы увидеть это складываем пополам лист бумаги пополам и прокалываем его иголкой. Разгибаем лист. Находим на нем две точки А и В. Проводим отрезок АВ и обозначаем буквой О его пересечение с прямой L. Отрезки АО и ВО равны.
В пространстве аналогом оси симметрии является плоскость симметрии. Отображение пространства на себя относительно плоскости называют зеркальной симметрией. Название это оправдано тем, что обе части фигуры, находящиеся по разные стороны от плоскости симметрии, похожи на некоторый объект и его отражение в зеркале.
У нас в поселке есть пруд, куда любят ходить отдыхать жители нашего села. На его берегу очень красиво. Тихо. Ничего не колышется. В воде отражаются берёзы, кусты, камыши. Вот она какая- зеркальная симметрия!
Такая симметрия встречается в цветах. Я попробовал повернуть ромашку, все получилось. Рассматриваю расположение листьев на ветке дерева, вижу, что один лист не только находится на расстоянии от другого, но и повёрнут вокруг оси ствола. Зачем? В энциклопедии написано, что листья располагаются на стволе по винтовой линии (принцип винтовой симметрии), чтобы не заслонять друг от друга солнечный свет.
Переносная симметрия. Если при переносе плоской фигуры F вдоль заданной прямой АВ на расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом.
Симметрия в математике
Симметрия встречается и на наших обычных уроках математики, например:
В геометрических фигурах: квадрате, прямоугольнике, треугольнике, круге.
Зеркальная симметрия в числах.
Числа, состоящие из цифр 8 и 0 симметричны.
Так же симметричны знаки арифметических действий, скобки двойные и фигурные:
+ = : ( ) < >[ ] Х
При изучении таблицы умножения и деления, мы увидели, что числа и ответы в ней расположены симметрично относительно оси симметрии-диагонали.
Симметрия в русском языке
На уроке русского языка мы заметили, что тоже встречается симметрия, например,:
Зеркальная анаграмма — разновидность анаграммы, фраза (или одно слово) получающаяся прочтением другой фразы в обратном порядке, например, «вор» — «ров».
Примеры зеркальных анаграмм
Зеркальные анаграммы похожи на палиндромы, но у палиндромов смысл при обратном прочтении не меняется (Приложение 1).
Шалаш, казак, радар, кок, Анна, поп, Алла.
А роза упала на лапу Азора.
Самый короткий палиндром в русском языке состоит всего из одной буквы — О!.
При подчеркивании членов предложения:
Сказуемое дополнение определение обстоятельство
В нашем учебнике по русскому языку используются такие условные обозначения, они симметричны:
Симметрия в окружающем мире
На уроках «Окружающий мир» мы изучаем живую и неживую природу.
Также примеры симметрии можно найти при рассмотрении растений.
Центральная симметрия Осевая симметрия
Мы заметили симметрию, рассматривая флаги разных государств.
Канада Азербайджан Великобритания
Человек так же является объектом живой природы. И мне стало интересно, а симметрично ли лицо человека? Для того, чтобы найти ответ на этот вопрос, мы проведем эксперимент.
Проводим вертикальную ось симметрии:
Копируем левую половинку. Так же поступили и с правой.
Совместили две левые половинки:
Совместили две правые половинки:
Проведя эксперимент, мы пришли к выводу, что лицо человека не симметрично, как кажется на первый взгляд.
Симметрия вокруг нас
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням, средневековым замкам, современным зданиям она придает гармоничность и законченность. Симметрия буквально пронизывает весь окружающий нас мир.
Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией.
Симметрия в технике наблюдается очень часто. Я думаю, люди это делают, потому что такой техникой удобнее пользоваться.
Симметрия используется и в быту, например, орнаменты и бордюры, посуда, предметы интерьера, одежда.
Симметрия встречается даже в поэзии и музыке.
Композитор в своей симфонии может по нескольку раз возвращаться к одной и той же теме, постепенно раскрывая ее.
В стихотворениях подразумевается симметрия чередования рифм, ударных слогов.
Все ярко, все бело кругом.
На стеклах легкие узоры,
Сорок веселых на дворе,
Деревья в зимнем серебре,
И мягко устланные горы
Зимы блистательным ковром.
Пушкин А.С. «Евгений Онегин»
Таким образом, я понял, что симметрия в моей жизни встречается повсюду, надо только быть внимательным и наблюдательным.
Мы познакомились с понятием симметрии и ее видами.
Теперь я задумался, а какую роль играет симметричность?
Я обратился с просьбой к ребятам, помочь выполнить задание.
Задание: Необходимо дорисовать симметричную половинку и несимметричную. Сделать вывод (Приложение 2).
Вывод: На этих рисунках симметричные объекты выглядят гармоничнее, чем асимметричные.
При этом, незначительные отклонения от симметрии придают объекту индивидуальность, и это тоже хорошо. Например, если бы все ёлки были полностью симметричными, то еловый лес вряд ли бы нам понравился. А небольшие отклонения от симметрии позволили превратить вазу в кувшин.
Симметрия веками оставалась тем свойством, которое занимало умы философов, астрономов, математиков, художников, архитекторов, и мы с большим удовольствием начали заниматься изучением симметрии.
В ходе данной работы мы познакомились с несколькими видами симметрии: «зеркальная», осевая и центральная. Нашли, где она прячется и поняли, что симметрия встречается везде: в живой и неживой природе, в технике, науке, искусстве, архитектуре, в быту. С симметрией мы встречаемся и в школе на всех уроках.
Мы считаем всё симметричное красивым, потому что симметрия — это порядок и устойчивость, а человек всегда стремится к порядку и гармонии. Но в окружающем нас мире нет абсолютной симметрии, и это мы выяснили в результате эксперимента с фотографией.
Исследователи доказали, что небольшие отклонения от симметрии придают индивидуальность объекту и делают его более интересным. Небольшие отклонения от симметрии допускаются и в архитектуре, одежде, прическах, украшения и т.д. Значительные же отклонения от симметрии считаются некрасивыми и часто не принимаются человеком.
Симметрия играет огромную роль в архитектуре, музыке, живописи, технике и в природе. Об этом сказано в одном стихотворении:
О, симметрия! Гимн тебе пою!Тебя повсюду в мире узнаю.Ты в Эйфелевой башне, в малой мошке,Ты в елочке, что у лесной дорожки.С тобою в дружбе и тюльпан, и роза,И снежный рой – творение мороза!
В результате проведённого исследования были достигнуты все цели и задачи. Работа была интересной и полезной. Своими знаниями я поделюсь с одноклассниками и другими ребятами начальной школы.
Список используемых источнтков
1.Вульф Г.В. Симметрия и ее проявления в природе. М., Изд. Отд. Нар.ком. Просвещение, 1991
2. Гаспаров М.Л. Очерк истории русского стиха: метрика, ритмика, рифма, строфика. М., 1984
3. Детский журнал «Смекалочка», № 7, март 2013 г.
5. Тарасов Л. Этот удивительно симметричный мир. – М.: Просвещение, 1982.
6. Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. М., 1972.
Аргентина манит негра.
А роза упала на лапу Азора.
Я с уколов – еле волокуся.
Лёша на полке клопа нашёл.
Лилипут сома на мосту пилил.
Я нем: лис укусил меня!
А кобыле цена – дана, да не целы бока!
А за работу – дадут? – Оба раза!
А муза – раба разума.
Я радую тетю – дядю ударя, Я радую дядю – тетю ударя.
Но невидим архангел, мороз узором лег на храм, и дивен он.
Презентация к проекту на»Центральная и осевая симметрия в жизни человека»
Описание презентации по отдельным слайдам:
Описание слайда:
Выполнила:
ученица 9«А» класса
Абрамова Ирина
Руководитель:
Терещенко Светлана Васильевна
учитель математики первой квалификационной категории
Описание слайда:
Цель:
Рассмотреть осевую и центральную симметрии и примеры их в природе
Задачи:
Что такое симметрия
Рассмотреть осевую и центральную симметрии
Найти симметрию в окружающем мире.
Показать, действительно ли нас окружают симметричные предметы.
Определить значение симметрии и ее использование в жизни.
Описание слайда:
Описание слайда:
Восхищаясь красотой окружающего мира, мы не задумываемся, что лежит в основе этой красоты.
Во-первых, мы с вами живём в симметричном мире, который обусловлен условиями жизни на планете Земля. Может быть, человек подсознательно понимает, что симметрия это форма устойчивости, а значит существования на нашей планете.
Во-вторых, окружающие человека люди, растения симметричны. Но если посмотреть поближе, то можно увидеть, что фигуры только почти симметричны. Но это не всегда воспринимает глаз человека. Глаз человека постепенно привыкает видеть симметричные объекты. Они воспринимаются, как гармоничные и совершенные.
Описание слайда:
Симметрия является одной из наиболее фундаментальных и одной из наиболее общих закономерностей мироздания: неживой, живой природы и общества. С ней мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Действительно симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Получается, что симметрия – это уравновешенность, упорядоченность, красота, совершенство. Она многообразна, вездесуща. Она создает красоту и гармонию. Симметрия буквально пронизывает весь окружающий нас мир, именно поэтому выбранная мной тема всегда будет актуальной.
Описание слайда:
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.
Описание слайда:
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно прямой а:
1. Для этого проведём из вершин треугольника ABC прямые, перпендикулярные оси симметрии и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Фигуры, симметричные относительно прямой, равны.
Описание слайда:
Описание слайда:
Описание слайда:
1.2 ЦЕНТРАЛЬНАЯ СИММЕТРИЯ.
Симметрию относительно точки называют центральной симметрией.
Точки M и M1 симметричны относительно некоторой точки O, если точка O является серединой отрезка MM1.
Точка O называется центром симметрии.
Описание слайда:
Алгоритм построения центрально-симметричных фигур.
Построим треугольник A1B1C1, симметричный треугольнику ABC, относительно центра (точки) O:
1. Для этого соединим точки A, B, C с центром O и продолжим эти отрезки;
2. Измерим отрезки AO, BO, COи отложим с другой стороны от точки O, равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.
Описание слайда:
Описание слайда:
III. Симметрия у человека
Человеческое тело обладает билатеральной симметрией (внешний облик и строение скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом. Тело человека построено по принципу двусторонней симметрии.
Большинство из нас рассматривает мозг как единую структуру, в действительности он разделён на две половины.
Эти две части – два полушария – плотно прилегают друг к другу. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого
Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое — левую сторону.
Описание слайда:
Описание слайда:
Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Описание слайда:
II. Симметрия в жизни растений
Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка, которая принципиально невозможна в периодических структурах неживой природы.
Посмотрим на кленовый лист. Кленовый лист симметричен. Если перегнуть его по среднему вертикальному стебельку-прожилке, то получившиеся части листа совпадут друг с другом. И перед нами две половинки – правая и левая! Можно провести опыт и с зеркалом; отражение в зеркале дополнит половину кленового листа до целого. Кленовый лист обладает зеркальной симметрией, и, если его нарисовать на листке бумаги, то полученная плоская фигура будет иметь ось симметрии.
Описание слайда:
Симметрию можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки.
Описание слайда:
Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.