примеры дизъюнкции в жизни
Урок на тему «Логические операции. Дизъюнкция»
Следующая логическая операция, которую мы рассмотрим после конъюнкции — дизъюнкция. Часто можно встретить другие названия этой операции — логическое сложение, логическое ИЛИ или просто ИЛИ.
В естественном языке дизъюнкция заменяется союзом ИЛИ.
Дизъюнкция, как и конъюнкция — бинарная операция, т. е. для нее необходимо два операнда.
Рассмотрим пример. Пусть есть два высказывания: A = «Париж — столица Франции» и B = «Сегодня пасмурно«. Тогда дизъюнкция этих высказываний будет выглядеть так «Париж — столица Франции ИЛИ сегодня пасмурно «, а обозначаться так:
Так как на клавиатуре нет символа дизъюнкция, его можно набрать из бэкслэша ( \ ) и слэша ( / ) — получится \/ — похоже на обозначение дизъюнкции.
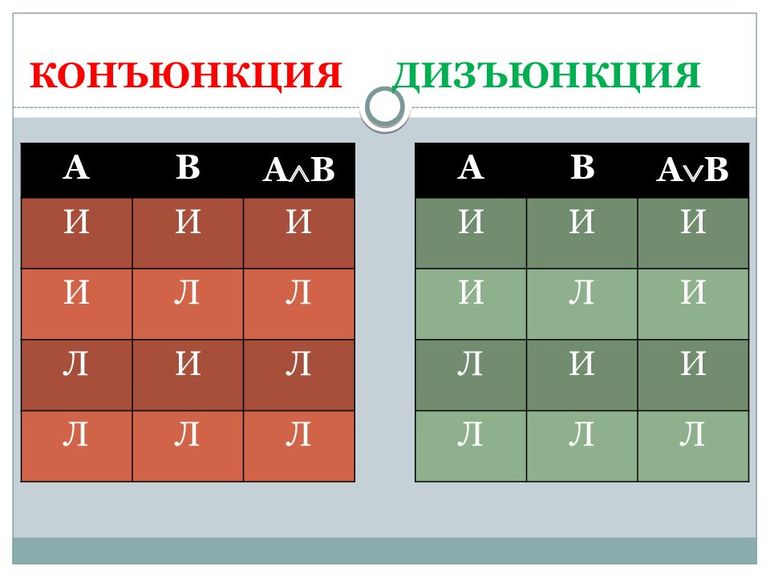
Таблица истинности для дизъюнкции выглядит так:
| A | B | A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
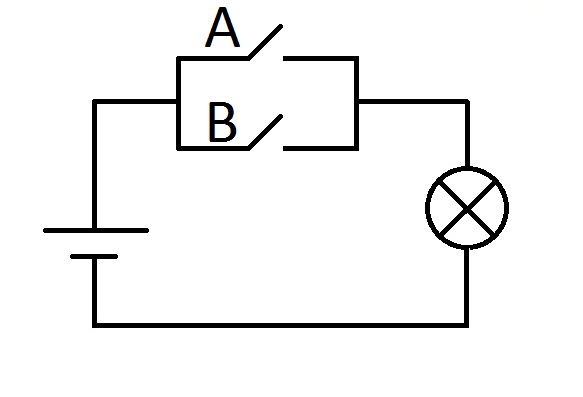
Запомнить таблицу довольно просто — дизъюнкция ложна только в одном случае — когда оба исходных высказывания ложны. Так же можно запомнить таблицу истинности для дизъюнкции, если представить ее электрический аналог — два параллельно включенных выключателя:
Электрический аналог дизъюнкции
По схеме сразу понятно, что лампочка будет гореть когда замкнуты оба выключателя, либо хотя бы один из них — аналогично дизъюнкции.
Автор: Александр Чернышов
Оцените статью, это очень поможет развитию сайта.
Дизъюнкция
Логическая операция Дизъюнкция — бинарная операция над высказываниями, результатом которой является истинное высказывание в случаях, когда среди исходных высказываний есть хотя бы одно истинное. Дизъюнкция ложна, если оба исходных высказывания ложны.
Другие названия дизъюнкции — логическое сложение, логическое ИЛИ или просто ИЛИ.
Дизъюнкция изучается в информатике при рассмотрении раздела алгебра логики.
В естественных языках дизъюнкцию заменяют союзом «или«.
В языках программирования для дизъюнкции используют обозначение ‘ or ‘ или одинарной (двойной) вертикальной чертной ‘ | ‘ (либо ‘ || ‘) (например, x 5 или a>=10 || a ).
Как набрать знак дизъюнкцию на клавиатуре
Так как на клавиатуре нет знака дизъюнкции (∨), ее удобно набирать используя комбинацию символов обратный слэш и слэш \/.
Таблица истинности для дизъюнкции
Истинность дизъюнкции определяется ее таблицей истинности.
| A | B | A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Дизъюнкция и круги Эйлера
Результатом дизъюнкции является как область пересечения высказываний, там и области самих исходных высказываний.
Электрический аналог дизъюнкции
Представим, что выключатели A и B — это высказывания, причем 0 — выключатель разомкнут, 1 — выключатель замкнут. Лампа символизирует дизъюнкцию. Когда она не горит — 0, горящая лампа — 1. Тогда становится очевидным, что лампа будет гореть если хотя бы один (и оба сразу) выключатель будет замкнут, что полностью соотносится с таблицей истинности для дизъюнкции.
Конъюнкция и дизъюнкция
Конъюнкция, дизъюнкция эквивалентность, инверсия, импликация — сложные для запоминания и понимания термины логики, науки, которая и сама по себе сложная для освоения. Но при ближайшем рассмотрении все слова оказываются более простыми, но обозначают совершенно не простые понятия. Используются термины не только в логике, но и в информатике. Объясняется это тем, что архитектура компьютера построена на понятиях математической логики.
Логика применима для решения задач по геометрии, физике, теории вероятности, понимания некоторых противоречивых речевых оборотов и сложных для непрофессионала научных текстов. Для понимания терминов и сферы их применимости изучим несколько вспомогательных понятий:
Если вы еще не запутались в этих терминах, перейдем к сути вопроса. Первое в нашем списке слово «конъюнкция». Это одно из сложных логических выражений, в котором обе составные части должны быть истинными, чтобы сказанное являлось истиной. Если одна из частей ложна, то ложно все выражение. Для иллюстрации используют таблицу:
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
В тексте конъюнкция обозначается простой формулой F = A & B. Часто конъюнкцию называют логическим умножением, по аналогии с математическим действием. Если один из множителей ноль, то результат всегда нулевой. В таблице показаны все возможные комбинации исходных данных для выбранной операции. На базе таблицы истинности можно проанализировать любое сложное высказывание. В предложении конъюнкция выражается союзом «и», который соединяет два высказывания. Вместо «и» можно использовать запятую.
Пример — «Рубильник на подстанции включен, и в комнате выключатель включен — люстра светит».
Если одно из выражений ложное, то света в комнате не будет.
Дизъюнкция, логическое сложение, которое подчиняется правилам математического сложения. Если одно из слагаемых истина (то есть 1) то результат получается 1 (в математике также возможен результат 2, но в логике обозначаем 1, как истинное выражение). Если оба исходных понятия ложные (0), то и результат не может быть истиной (1). Таблица для дизъюнкции выглядит так:
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
А формула принимает вид: F = A + B.
Итак, сложные и непонятные слова конъюнкция и дизъюнкция приняли образ вполне понятных действий умножения и сложения, знакомых даже ученикам младших классов. В письменной речи используют союз «или». Но в логике он несколько отличается от филологического значения. В филологии «или» показывает, что правильна одна из частей предложения, а в логике — что правильны или ложны одна из частей, и обе части одновременно (все предложение).
«Если температуры нет, или анализы покажут, что воспаления нет, то пациент здоров».
Попутно рассмотрим другие понятия логики. Одно из сложных для понимания — инверсия, или логическое отрицание. Если начальное утверждение правильное, то результат отрицания будет ложным, и, наоборот, при ложном исходном выражении, отрицание будет настоящим. В письменной речи инверсия выражается словами «НЕ», «НЕВЕРНО, ЧТО». Таблица инверсии:
«Вы утверждаете, что все ученики 9 класса отличники, НЕВЕРНО, ЧТО все ученики 9 класса отличники». (Не все ученики 9 класса отличники).
Импликация — сложное выражение, в результате которого всегда получается единица (истина). В письменной речи аналогом импликации является связка если…, то. Пример «Если твердое тело тереть о жесткую поверхность, то оно нагревается». «Если замечены изменения в экономической ситуации, то изменится и политика». Таблица импликации:
| А | В | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Можно заметить, что в одной строке результат «0». Это исключение, когда из истинного утверждения не может получиться ложный результат.
Эквивалентность — операция в логике, при которой истина получается только в том случае, если обе части выражения истинны:
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
В сложном логическом выражении существует определенный порядок выполнения операций:
Если нужно изменить этот порядок, то используют скобки.
Общие сведения
Булева алгебра — раздел математического анализа, изучающий истинность логических утверждений. Ее открыл Д. Буль в ХIХ веке. Алгебра логики получила практическое применение только в ХХ веке при проектировании различных элементов персонального компьютера. Дисциплина доказывает истинность или ложность тождеств логического типа математическим путем с применением специальных таблиц.
Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).
Операторы сравнения
Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t 0). При использовании логического отрицания условие выглядит короче: t=!0.
Приоритеты вычислений
При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:
Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:
Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.
Примеры решений
В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).
Решать задание нужно по такому алгоритму:
Следующий пример будет сложнее, поскольку выражение ¬ < ¬[ ¬((S|0)&¬(T|S)& ¬(S&(T&S)) ]& ¬(S&S) >следует упростить, а затем составить таблицу. Задача решается по такой методике:
Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.
Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.
Конъюнкция и дизъюнкция — правила и примеры решения в математике
В информатике существует специальная дисциплина, рассматривающая логические операции отрицания, конъюнкции и дизъюнкции. В математике это направление называется булевой алгеброй и применяется для построения алгоритмов, проверяющих различные условия и соответствия. Специалисты в области информационных технологий рекомендуют перед практическим решением примеров получить теоретические знания.
Общие сведения
Булева алгебра — раздел математического анализа, изучающий истинность логических утверждений. Ее открыл Д. Буль в ХIХ веке. Алгебра логики получила практическое применение только в ХХ веке при проектировании различных элементов персонального компьютера. Дисциплина доказывает истинность или ложность тождеств логического типа математическим путем с применением специальных таблиц.
Следует отметить, что логическое тождество является определенной функцией, принимающей значения 0 или 1 в зависимости от ее элементов. В алгебре логики значения имеют следующие названия: 0 — ЛОЖЬ (FALSE) и 1 — ИСТИНА (TRUE).
Операторы сравнения
Следует отметить, что в этих примерах получается истинное значение, поскольку условие выполняется. Однако в информатике при построении алгоритмов используются методы ветвления. Они представляют собой такую конструкцию: ЕСЛИ (a>b), ТО a+b. ИНАЧЕ (a*b). Читается запись следующим образом: в том случае, когда значение а больше b, нужно сложить оба числа, а иначе (a Логические операции
Операции логического типа очень часто применяются при построении выражений, используемых в программировании. К ним относятся следующие:
Однако булева алгебра не ограничивается только ими, поскольку существуют и другие их производные. Для каждой из трех составляются определенные таблицы истинности, которые каждый раз необходимо строить для получения результата вычисления логических выражений. Специалисты рекомендуют отдельно на листе картона перечертить таблицы всех логических операций.
Функция конъюнкции
Конъюнкция — операция логического умножения, которая будет истинным при достоверности каждого выражения. Ее обозначение — символ конъюнктора «&». Записывается следующим образом: S&T, где S и T — логические тождества или конкретные значения. Операция имеет такие особенности: только при равенстве всех элементов 1 значение выражения является истинным, а в других случаях — ложью. Для проверки необходимо составить таблицу значений логического тождества:
| S | T | S&T |
| 0 | 0 | F |
| 0 | 1 | F |
| 1 | 0 | F |
| 1 | 1 | T |
Таблица 1. Значение функции в зависимости от логических переменных.
Из таблицы 1 видно, что выражение S&T принимает только TRUE при всех истинных значениях переменных. Если рассматривать алгебру, то можно провести аналогию между логическим и обыкновенным умножениями. Например, произведение двух чисел S*T, которые для удобства сравнения принимают значения 0 или 1.
Если сравнивать два результата, то они будут идентичны. Следовательно, для правильного построения таблицы для конъюнкции нужно руководствоваться аналогичной операцией умножения.
Информация о дизъюнкции
В булевой алгебре операция логического сложения называется дизъюнкцией. Обозначается она символом, который называется дизъюнктором (V или I). Логическое тождество, содержащее два элемента, имеет такой вид: SVT. Операция имеет только ложное значение при равенстве S и T нулю. Для нее нужно также строить специальную таблицу:
| S | T | Результат — S|T |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таблица 2. Истинность операции дизъюнкции SVT.
Операция аналогична сложению в алгебре, хотя имеются некоторые отличия. Чтобы убедиться в этом, требуется выполнить определенное действие — построить специальную таблицу результатов для алгебраического сложения нулей и единиц.
Если рассмотреть результаты в последнем случае, то можно сделать вывод о схожести сложения и дизъюнкции. Однако в последней строке алгебраической суммы есть некоторое несоответствие — 2. Это показывает, какое переполнение разряда происходит в булевой алгебре. В последней происходит переход с одного разряда в другой.
Булево отрицание
В алгебре логики применяется также операция отрицания, которую также называют инверсией. Суть ее заключается в том, что при истинном значении выражения под знаком инверсии получается ложный результат, а при ложном — истина. Обозначается она символом инверсии «¬», а записывается в таком виде ¬(S). Для демонстрации операции необходимо ознакомиться с таблицей:
| Исходное выражение, S | Результат, ¬(S) |
| 0 | T |
| 1 | F |
Таблица 3. Истинность ¬(S).
Например, если необходимо указывать несколько тождеств логического вида, то при помощи отрицания можно использовать только одно. Для примера необходимо написать, что число не равно 0: (t 0). При использовании логического отрицания условие выглядит короче: t=!0.
Приоритеты вычислений
При решении выражений булевского типа, как и в алгебре, существуют определенные приоритеты. Каждая операция обладает определенным из них. Наибольшей степенью пользуется конъюнкция, средней — дизъюнкция. Наименьшим приоритетом обладает логическое отрицание. Однако эту особенность можно поменять при помощи группировки элементов в выражениях, которая производится скобками. С учетом этих особенностей алгоритм решения тождества имеет следующий вид:
Иногда бывают задачи, в которых следует упрощать выражение. Для этой цели следует знать некоторые особенности:
Этих правил достаточно для упрощения булевского выражения. Следует отметить, что перед построением булевской таблицы требуется с самого начала упростить исходное тождество.
Примеры решений
В первом простом примере требуется составить таблицу булевского типа для выражения S&(S|T)|T&S|¬(T&S).
Решать задание нужно по такому алгоритму:
Следующий пример будет сложнее, поскольку выражение ¬ < ¬[ ¬((S|0)&¬(T|S)& ¬(S&(T&S)) ]& ¬(S&S) >следует упростить, а затем составить таблицу. Задача решается по такой методике:
Следует отметить, что исходное логическое выражение необходимо на начальном этапе решения упростить, а затем строить таблицу. В этом возможно убедиться на основании приведенного примера, в котором сокращается одна переменная.
Таким образом, для решения выражения, содержащего логические операции конъюнкции, дизъюнкции и инверсии, необходимо его упростить, а затем разбить на простые элементы.