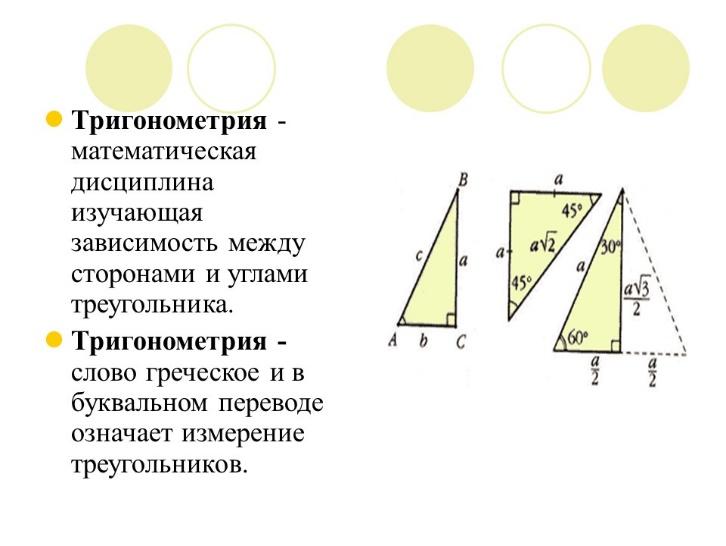
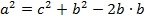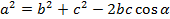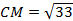применение теоремы косинусов в жизни человека
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
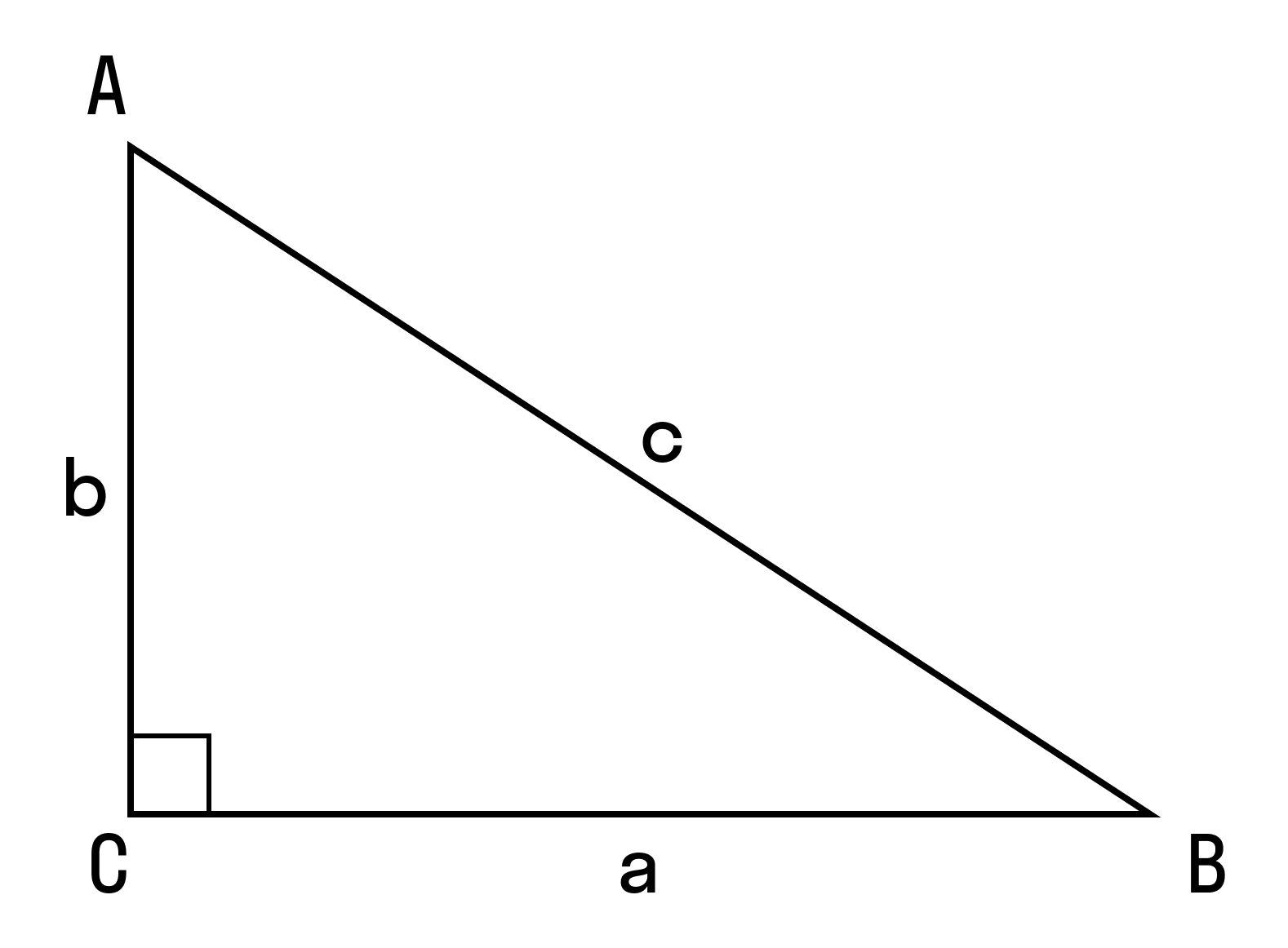
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
К полученному выражению прибавим и отнимем квадрат второго катета:
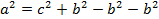
Но так как b = c * cos α, то
Эту формулу мы получили для катетов в прямоугольном треугольнике, но аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника.
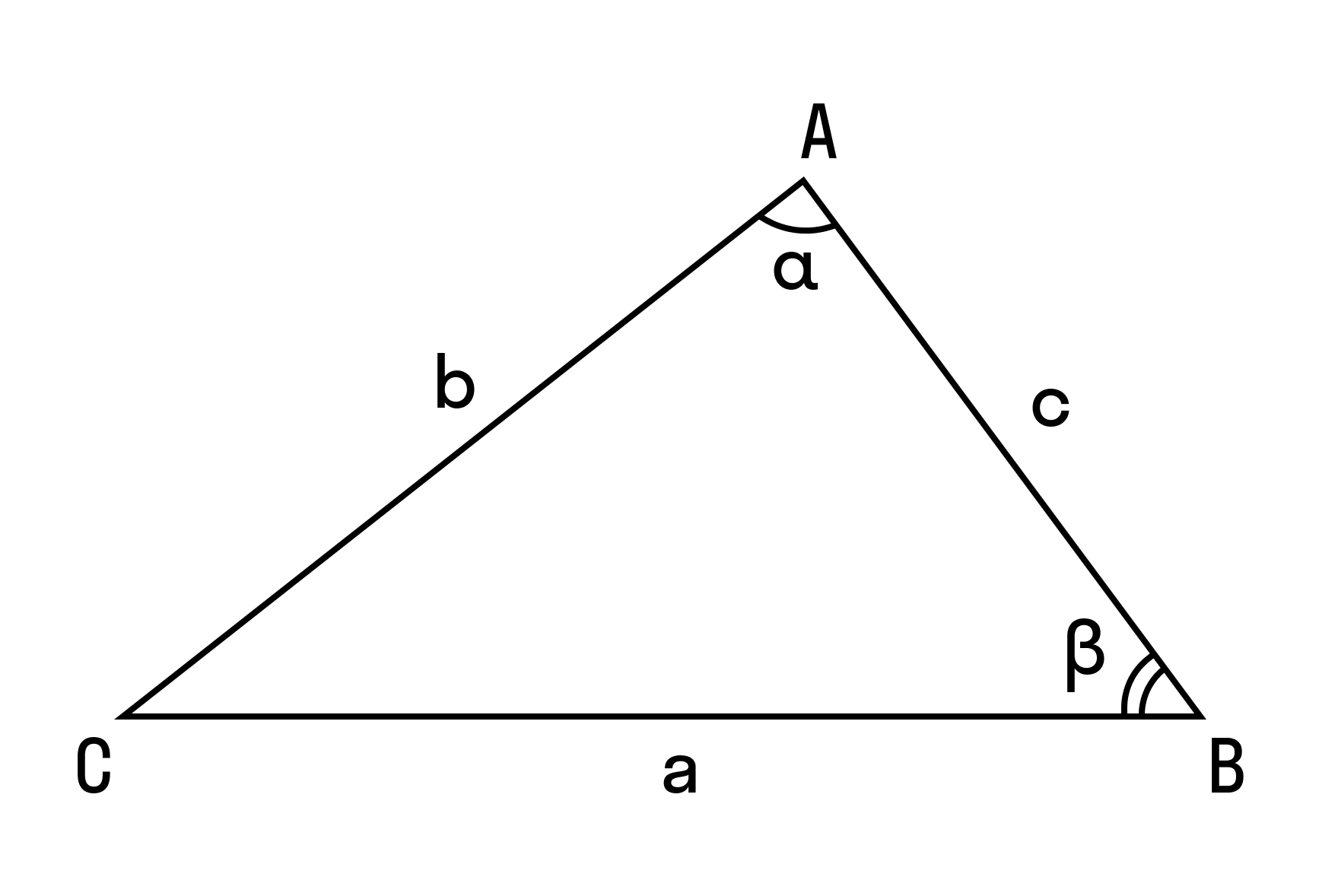
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Следствие из теоремы косинусов: теорему косинусов также можно использовать для определения косинуса угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Таким образом, теорема косинусов обобщает теорему Пифагора. Закон косинуса может быть использован для любого вида треугольника.
Описание формулы косинуса угла из теоремы косинусов
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Тригонометрия в окружающем нас мире и жизни человека»
Выбранный для просмотра документ Данилова Т.В.-сценарий.doc
МКОУ «Ненецкая общеобразовательная средняя школа – интернат им. А.П.Пырерки»
Данилова Татьяна Владимировна
Обоснование актуальности проекта.
Школьник в 14-15 лет не всегда знает, куда пойдет учиться и где будет работать.
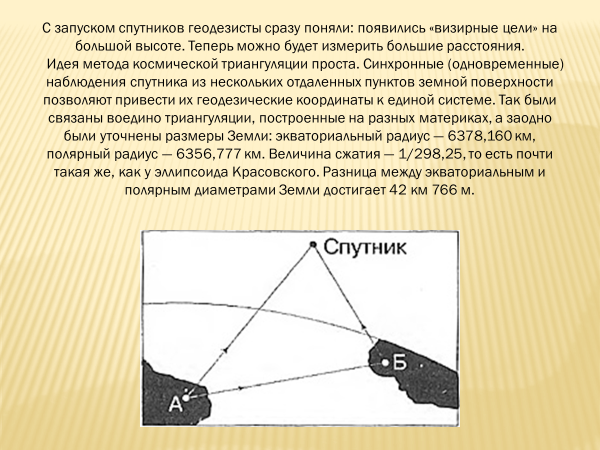
Для некоторых профессий ее знание необходимо, т.к. позволяет измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Принципы тригонометрии, используются и в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Определение предмета исследования
Почему знания тригонометрии необходимы для современного человека?
Связь тригонометрии с реальной жизнью.
Проблемный вопрос
1. Какие понятия тригонометрии чаще всего используются в реальной жизни?
2. Какую роль играет тригонометрия в астрономии, физике, биологии и медицине?
3. Как связаны архитектура, музыка и тригонометрия?
Большинство физических явлений природы, физиологический процессов, закономерностей в музыке и искусстве можно описать с помощью тригонометрии и тригонометрических функций.
Зачатки тригонометрических познаний зародились в древности. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.
Истоки тригонометрии берут начало в древнем Египте, Вавилонии и долине Инда более 3000 лет назад.
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Птолемеем.
Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна. По звездам вычисляли местонахождение корабля в море.
Следующий шаг в развитии тригонометрии был сделан индийцами в период с V по XII в.
В XVII – XIX вв. тригонометрия становится одной из глав математического анализа.
Она находит большое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов.
Жан Фурье доказал, что всякое периодическое движение может быть представлено (с любой степенью точности) в виде суммы простых гармонических колебаний.
Стадии развития тригонометрии:
Тригонометрия была вызвана к жизни необходимостью производить измерения углов.
Необходимость табулировать значения вводимых тригонометрических функций.
Тригонометрические функции превращались в самостоятельные объекты исследований.
В XVIII в. тригонометрические функции были включены
в систему математического анализа.
Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)
Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).
Тригонометрия в физике:
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.
Тригонометрия в природе.
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Тригонометрия и тригонометрические функции в медицине и биологии.
Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
диатоническая гамма 2:3:5
Тригонометрия в архитектуре
Детская школа Гауди в Барселоне
Страховая корпорация Swiss Re в Лондоне
Феликс Кандела Ресторан в Лос-Манантиалесе
Мы привели лишь малую часть того, где можно встретить тригонометрические функции.. Мы выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Мы доказали, что тригонометрия тесно связана с физикой, встречается в природе, медицине. Можно приводить бесконечно много примеров периодических процессов живой и неживой природы. Все периодические процессы можно описать с помощью тригонометрических функций и изобразить на графиках
Мы думаем, что тригонометрия нашла отражение в нашей жизни, и сферы,
в которых она играет важную роль, будут расширяться.
Выяснили, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
Доказали, что тригонометрия тесно связана с физикой, встречается в природе, музыке, астрономии и медицине.
Думаем, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.
Маслова Т.Н. «Справочник школьника по математике»
Программа Maple6, реализующий изображение графиков
История математики с Древнейших времен до начала XIX столетия в 3-х томах// под ред. А. П. Юшкевича. Москва, 1970г. – том 1-3 Э. Т. Бэлл Творцы математики.
Предшественники современной математики// под ред. С. Н. Ниро. Москва,1983г. А. Н. Тихонов, Д. П. Костомаров.
Рассказы о прикладной математике//Москва, 1979г. А. В. Волошинов. Математика и искусство// Москва, 1992г. Газета Математика. Приложение к газете от 1.09.98г.
Применение тригонометрии в жизни
Позволяет познакомить с тригонометрией,как прикладной наукой, заинтересовать учащихся
Содержимое разработки
Урок «Применение тригонометрии в жизни».
10 класс Учитель: Голубкова Елена Юрьевна.
Цели и задачи: Показать практическое применение тригонометрии, ее использование и значимость. Заинтересовать учащихся. Решить практические задачи.
— Определение тригонометрии, виды.
—Тригонометрия – раздел математики, изучающий зависимость между сторонами и углами треугольника, а также свойства тригонометрических функций и связь между ними.
—Сферическая геометрия – геометрическая дисциплина, изучающая свойства фигур на сфере. Аналогична в некоторой степени планиметрии. Большие круги на сфере, являясь геодезическими линиями, играют роль прямых на плоскости: через две точки сферы, не совпадающие с концами ее диаметра, проходит только одна большая окружность. В сферической геометрии нельзя провести параллельные прямые.
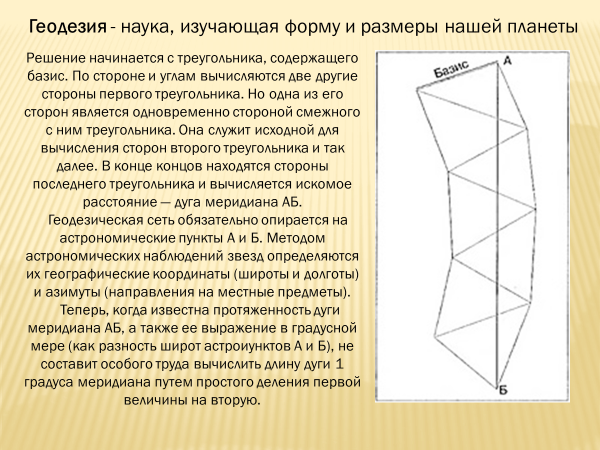
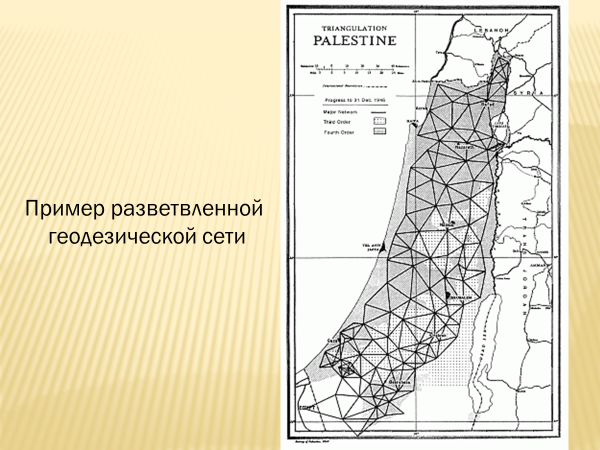
Применяется в геодезии, географии при составлении карт, астрономии при изучении небесной сферы, в мореплавании и др. областях знаний. Сферическая геометрия развивалась благодаря работам индийских и арабских ученых – Ариабхата, \/ в; Аль-Баттани, IX в, Абу-Аль Вефа, XI в. Изучали европейские математики Региомонтан, Непер, Меркатор и др. Особую роль сыграли работы Леонарда Эйлера, благодаря которому сферическая геометрия приобрела современный вид.
История тригонометрии как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобилось ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.
Историки полагают, что тригонометрию создали древние астрономы; немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, и в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности. Особенно полезными тригонометрические функции оказались при изучении колебательных процессов; на них основан также гармонический анализ функций и другие инструменты анализа. Томас Пейн в своей книге «Век Разума» (1794) назвал тригонометрию «душой науки».
Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.). Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э Вполне возможно, что китайцы открыли его независимо (см. «Математика в девяти книгах»); неясно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался
Несколько теорем тригонометрического характера содержат «Начала» Евклида (IV век до н. э.). В первой книге «Начал» теоремы 18 и 19 устанавливают, что большей стороне треугольника соответствует больший противолежащий угол — и обратно, большему углу соответствует бо́льшая сторона. Теоремы 20 и 22 формулируют «неравенство треугольника»: из трёх отрезков можно составить треугольник тогда и только тогда, когда длина каждого меньше суммы длин двух других. Теорема 32 доказывает, что сумма углов треугольника равна 180°.
Во второй книге «Начал» теорема 12 представляет собой словесный аналог теоремы косинусов
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.
Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам. Приведена теорема тангенсов для сферических треугольников, описано важное понятие полярного треугольника (впервые использованное в XI веке Ибн Ираком и ал-Джайяни). Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии.
Таким образом, к концу XIII века были открыты базовые теоремы, составляющие содержание тригонометрии:
— Выражение любой тригонометрической функции через любую другую.
— Формулы для синусов и косинусов кратных и половинных углов, а также для суммы и разности углов.
— Теоремы синусов и косинусов.
— Решение плоских и сферических треугольников
Из-за отсутствия алгебраической символики все перечисленные теоремы выражались в громоздкой словесной форме, но по существу были полностью эквивалентны современному их пониманию.
Развитие тригонометрии в Новое время стало чрезвычайно важным не только для астрономии и астрологии, но и для других приложений, в первую очередь артиллерии, оптики и навигации при дальних морских путешествиях. Поэтому после XVI века этой темой занимались многие выдающиеся учёные, в том числе Николай Коперник, Иоганн Кеплер, Франсуа Виет. Коперник посвятил тригонометрии две главы в своём трактате «О вращении небесных сфер» (1543). Вскоре (1551) появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″. Кеплер опубликовал труд «Оптическая часть астрономии» (1604).
Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера».
Реформы Леонарда Эйлера
Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному, и соответственно определил обратные функции. Если его предшественники понимали синус и прочие понятия геометрически, то есть как линии в круге или треугольнике, то после работ Эйлера <\displaystyle \sin x,
\operatorname
Тригонометрия в России
В России первые сведения о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л. Ф. Магницкого в 1703 году. В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М. Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
В конце XVIII века в Петербурге возникла авторитетная тригонометрическая школа (А. И. Лексель, Н. И. Фусс, Ф. И. Шуберт), которая внесла большой вклад в плоскую и сферическую тригонометрию.
В начале XIX века Н. И. Лобачевский добавил к плоской и сферической тригонометрии третий раздел — гиперболическую (для геометрии Лобачевского, первую работу в этой области опубликовал Ф. А. Тауринус в 1826 году). Лобачевский показал, что формулы сферической тригонометрии переходят в формулы гиперболической тригонометрии при замене длин сторон треугольника a, b, c на мнимые величины: ai, bi, ci — или, что эквивалентно, при замене тригонометрических функций на соответствующие гиперболические
Домашнее задание: Подобрать практические задачи, решаемые с
помощью тригонометрии. Подготовить доклад о развитии тригонометрии в