применение скалярного произведения векторов в жизни

Учимся вместе: математика

Выпуск № 71 от 2010-06-08
www.clearwords.ru
Количество человек, получивших этот выпуск: 1382

«Когда другому кажется, что ситуация чересчур запутана и почти невыносима, когда голова у него идёт кругом, посоветуйте ему посмотреть на ситуацию со стороны.
То, что он обнаруживает, как правило, покажется совершенно очевидным – когда он это увидит. После этого он сможет снова взяться за дело и справиться с ситуацией. Но если люди не видят чего-то сами, то это не будет по-настоящему реальным для них, и тогда никакие директивы, приказы и наказания не смогут вывести их из затруднения ». – Л Рон Хаббард

Скалярное произведение векторов

Мы рассмотрели такие понятия как «вектор» и «скаляр». Теперь, давайте рассмотрим как эти два понятия используются в математике и в жизни.

В частности, мы рассмотрим, что такое «скалярное произведение векторов». Особенно нас интересует не просто формулы, а как это используется на практике, и в чем физический смысл этого понятия.

Начнем объяснение этого термина с рассмотрения реальных ситуаций в жизни, чтобы вам было проще понять его суть.

Вы все наблюдали картину, когда человек, животное или какой-либо механизм перемещает груз из одного места в другое.

Посмотрите на примеры ниже:

\

В каждом примере имеется сила, которая перемещает груз на некоторое расстояние. Другими словами, совершается работа по перемещению груза из одного места в другое. Это количество работы может быть больше, может быть меньше. Все зависит от количества прилагаемого усилия. Количество работы, совершаемое одним человеко, будет отличаться от количества работы, которое будет совершать, например несколько человек или какой-либо механизм.

А можно ли измерить эту работу? Как найти числовое значение этой работы, и от чего оно зависит?

Чтобы ответить на эти вопросы, представим примеры, приведенные на фотографиях, в виде общей схемы. Нарисуем два вектора и перемещаемый груз. Один вектор (F) будет показывать приложенную силу (в наших примерах это сила человека или животного), а вектор (s) показывает путь перемещения предмета (автомобиль, тележка или повозка с грузом).

Вектор отражает направление движения, а также длину пути, которое проходит тело при перемещении. Очевидно, что чем больше прилагаемая сила, тем больше длину вектора (F) мы рисуем. Тоже самое можно сказать и о векторе S. Чем длиннее путь перемещения предмета, те больше длина вектора S.

Если связать силу и путь, то мы получим следующую зависимость одной величины от другой: чем больше приложенная сила, тем больше путь перемещения предмета. Если сказать простым языком, то 5 человек производят больше работы, и они на большее расстояние переместят, например, автомобиль или повозку с грузом, за тоже самое время, чем это сделает один человек.

Еще один фактор влияющий на длину пути перемещения, это угол приложения силы к перемещаемому грузу. На рисунке это угол α.

Итак, из вышесказанного сделаем вывод: количество работы по перемещению предмета будет складываться из количества прилагаемой силы, угла приложения этой силы и длинны пути перемещения.

Давайте переведем это на язык математики: количество работы зависит от длинны вектора F, длинны вектора s и угла α.

Поскольку длина каждого вектора это число или скаляр, а угол между ними можно выразить через отношения длин этих векторов (S/F), а это косинус угла α, то мы получаем следующее определение:

Определение

Cкалярное произведение векторов — это произведение их длин на косинус угла между ними.

Используя математические символы, запишем это в виде формулы:

В результате умножения длины вектора F на длину вектора S и на косинус угла между ними, мы получаем скаляр или просто определенное число.

В рассмотренных выше примерах, это число показывает количество совершаемой работы по перемещению тела из одной точки в другу. В других областях применения это число будет иметь другой смысл.

Примеры использования

Скалярное произведение векторов широко используется в математике, физике, а так же в других прикладных науках.

Этимология

Слово «скаляр» образовано от латинского слова scalaris — ступенчатый.

Задание

Составьте сами несколько предложений с этим словом, чтобы до конца усвоить его.

В следующих уроках мы рассмотрим и другие слова, которые используются в математике. Шаг за шагом мы с вами разберем все основные слова, и вам станет многое понятно в этой науке, и она перестанет быть чем-то запутанным и сложным.

ПОМОЩЬ ПРОЯСНИТЕЛЯ СЛОВ (РЕПЕТИТОРА) ПО МАТЕМАТИКЕ, РУССКОМУ ЯЗЫКУ
и другим школьным предметам!
Результат работы нашего прояснителя слов – ЗНАНИЯ вашего ребенка!
Звоните и записывайтесь на бесплатное тестирование и консультацию.
Телефоны: 8(925)507-86-83, 8(901)572-50-88, (495)6806673, www.clearwords.ru

Заявку на участие вы можете отправить или позвонить по телефонам: 507-86-83 и 8(901)572-50-88

Отзывы после просветительской кампании «Проясняй слова, Россия!»

«Акция очень необходима для понимания и прояснения слов, которые встречаются при обучении, в обиходе разговорной речи. Прояснение слов необходимо для глубокого понимания изучаемого материала и в общении.»

ПОМОЩЬ ПРОЯСНИТЕЛЯ СЛОВ (РЕПЕТИТОРА) ПО МАТЕМАТИКЕ, РУССКОМУ ЯЗЫКУ
и другим школьным предметам!
Результат работы нашего прояснителя слов – ЗНАНИЯ вашего ребенка!
Звоните и записывайтесь на бесплатное тестирование и консультацию.
Телефоны: 8(925)507-86-83, 8(901)572-50-88, (495)6806673, www.clearwords.ru

Источник

Применение векторов в повседневной жизни

С понятием вектора мы встречаемся чаще,чем сами подозреваем. В данной работе я постаралась максимально изучить, в каких же сферах мы взаимодействуем с ним.

Просмотр содержимого документа
«Применение векторов в повседневной жизни»

С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор. Далее, в процессе работы над данным проектом, я приведу ещё множество не менее интересных примеров векторов.

Вообще, я считаю, что математика – это интереснейшая наука, в познании которой нет границ. Я выбрала тему о векторах не случайно, меня очень заинтересовало то, что понятие «вектор» выходит далеко за рамки одной науки, а именно математики, и окружает нас практически везде. Таким образом, каждый человек должен знать, что такое вектор, поэтому, я думаю, что эта тема весьма актуальна. В психологии, биологии, экономике и многих других науках употребляют понятие «вектор». Подробнее об этом я расскажу позже.

Целями данного проекта являются приобретение навыков работы с векторами, умение видеть необычное в обычном, выработка внимательного отношения к окружающему миру.

История возникновения понятия вектор

Одним из фундаментальных понятий современной математики является вектор. Эволюция понятия вектора осуществлялась благодаря широкому использованию этого понятия в различных областях математики, механики, а так же в технике.

Вектор относительно новое математическое понятие. Сам термин «вектор» впервые появился в 1845 году у ирландского математика и астронома Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат и термин «скаляр», «скалярное произведение», «векторное произведение». Почти одновременно с ним исследования в том же направлении, но с другой точки зрения вёл немецкий математик Герман Грассман (1809 – 1877). Англичанин Уильям Клиффорд (1845 – 1879) сумел объединить два подхода в рамках общей теории, включающий в себя и обычное векторное исчисление. А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу.

Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением. Например, некоторые физические величины, такие, как сила, скорость, ускорение и др., характеризуются не только числовым значением, но и направлением. В связи с этим указанные физические величины удобно изображать направленными отрезками. В соответствии с требованиями новой программы по математике и физике понятие вектора стало одним из ведущих понятий школьного курса математики.[2]

Векторы в математике

Вектором называется направленный отрезок, который имеет начало и конец.[1]

Вектор с началом в точке А и концом в точке В принято обозначать как АВ. Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например .

Вектор в геометрии естественно сопоставляется переносу (параллельному переносу), что, очевидно, проясняет происхождение его названия (лат. vector, несущий). Действительно, каждый направленный отрезок однозначно определяет собой какой-то параллельный перенос плоскости или пространства: скажем, вектор АВ естественно определяет перенос, при котором точка А перейдет в точку В, также и обратно, параллельный перенос, при котором А переходит в В, определяет собой единственный направленный отрезок АВ.

Длиной вектора АВ называется длина отрезка АВ, её обычно обозначают АВ. Роль нуля среди векторов играет нулевой вектор, у которого начало и конец совпадают; ему, в отличие от других векторов, не приписывается никакого направления.

Два вектора называются коллинеарными, если они лежат на параллельных прямых, либо на одной прямой. Два вектора называются сонаправленными, если они коллинеарны и направлены в одну сторону, противоположно направленными, если коллинеарны и направлены в разные стороны.

Операции над векторами

Модулем вектора АВ называется число, равное длине отрезка АВ. Обозначается, как АВ. Через координаты вычисляется, как:

=+ +

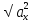
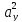
В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

)<\displaystyle <\vec >+<\vec >=(a_+b_,a_+b_,a_+b_)>

Для геометрического построения вектора суммы <\displaystyle <\vec >=<\vec >+<\vec >>c = используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов <\displaystyle <\vec >> и <\displaystyle <\vec >> некоторой точки будет тем же, что применение сразу одного переноса <\displaystyle <\vec >+<\vec >>, соответствующего этому правилу. Для сложения двух векторов<\displaystyle <\vec >> и <\displaystyle <\vec >> по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

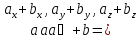
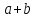
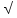
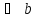
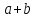
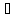
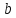
Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:

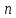
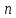
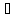
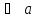
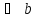
Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же <\displaystyle n>векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом <\displaystyle n>— го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Для сложения двух векторов <\displaystyle <\vec >> и <\displaystyle <\vec >> по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

‚ <\displaystyle <\vec >—<\vec >=(a_-b_,a_-b_,a_-b_)>

Для получения вектора разности <\displaystyle <\vec >=<\vec >—<\vec >> начала векторов соединяются и началом вектора <\displaystyle <\vec >> будет конец <\displaystyle <\vec >>, а концом — конец <\displaystyle <\vec >>. Если записать, используя точки векторов, то AC-AB=BC<\displaystyle <\overrightarrow >-<\overrightarrow >=<\overrightarrow >>.

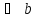
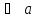
Умножение вектора на число

Скалярное произведение векторовСкалярное

Скалярным произведением называют число, которое получается при умножении вектора на вектор. Находится по формуле:

Скалярное произведение можно найти ещё через длину векторов и угол между ними.

Применение векторов в смежных науках Векторы в физике Векторы — мощный инструмент математики и физики. На языке векторов формулируются основные законы механики и электродинамики. Чтобы понимать физику, нужно научиться работать с векторами. В физике, как и в математике, вектор – это величина, которая характеризуется своим численным значением и направлением. В физике встречается немало важных величин, являющихся векторами, например сила, положение, скорость, ускорение, вращающий момент, импульс, напряженность электрического и магнитного полей. Векторы в литературе Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу сил равна нулю. А сила, как известно, векторная величина. Векторы в химии

Нередко даже великими учеными высказывалась мысль, что химическая реакция является вектором. Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают действие или явление, имеющее четкую направленность в пространстве и в конкретных условиях, отражаемое его величиной. Направление вектора в пространстве определяется углами, образующимися между вектором и координатными осями, а длина (величина) вектора – координатами его начала и конца.

Однако утверждение, что химическая реакция является вектором, до сих пор было неточно. Тем не менее основой этого утверждения служит следующее правило: «Любой химической реакции отвечает симметричное уравнение прямой в пространстве с текущими координатами в виде количеств веществ (молей), масс или объемов».

Все прямые химических реакций проходят через начало координат. Любую прямую в пространстве нетрудно выразить векторами, но поскольку прямая химической реакции проходит через начало системы координат, то можно принять, что вектор прямой химической реакции находится на самой прямой и называется радиус-вектором. Начало этого вектора совпадает с началом системы координат. Таким образом, можно сделать вывод: любая химическая реакция характеризуется положением ее вектора в пространстве. Векторы в биологии

Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы.

Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.

Векторы в экономике

Одним из разделов высшей математики является линейная алгебра. Ее элементы широко применяются при решении разнообразных задач экономического характера. Среди них важное место занимает понятие вектора.

Вектор представляет собой упорядоченную последовательность чисел. Числа в векторе с учетом их расположения по номеру в последовательности называются компонентами вектора. Отметим, векторы можно рассматривать в качестве элементов любой природы, в том числе и экономической. Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30 комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда производственную программу данной фабрики можно представить в виде вектора, где всё, что должна выпустить фабрика – это трехмерный вектор.

Векторы в психологии

На сегодняшний день имеется огромное количество информационных источников для самопознания, направлений психологии и саморазвития. И не трудно заметить, что все больше обретает популярность такое необычное направление, как системно-векторная психология, в ней существует 8 векторов.

Векторы в повседневной жизни

Я обратила внимание, что векторы, помимо точных наук, встречаются мне каждый день. Так, например, во время прогулки в парке, я заметила, что ель, оказывается, можно рассматривать как пример вектора в пространстве: нижняя её часть – начало вектора, а верхушка дерева является концом вектора. А вывески с изображением вектора при посещении больших магазинов помогают нам быстро найти тот или иной отдел и сэкономить время.

Векторы в знаках дорожного движения

Каждый день, выходя из дома, мы становимся участниками дорожного движения в роли пешехода либо в роли водителя. В наше время практически каждая семья имеет машину, что, разумеется, не может не отразиться на безопасности всех участников дорожного движения. И, чтобы избежать казусов на дороге, стоит соблюдать все правила дорожного движения. Но не стоит забывать того, что в жизни всё взаимосвязано и, даже в простейших предписывающих знаках дорожного движения, мы видим указательные стрелки движения, в математике называемые – векторами. Эти стрелки (векторы) указывают нам направления движения, стороны движения, стороны объезда, и ещё многое другое. Всю эту информацию можно прочитать на знаках дорожного движения на обочинах дорог.

Базовое понятие «вектор», рассмотренное нами ещё на уроках математики в школе, является основой для изучения в разделах общей химии, общей биологии, физики и других наук. Я наблюдаю необходимость векторов в жизни, которые помогают найти нужный объект, сэкономить время, они выполняют предписывающую функцию в знаках дорожного движения.

Каждый человек постоянно сталкивается с векторами в повседневной жизни.

Векторы необходимы нам для изучения не только математики, но и других наук.

Источник