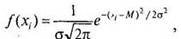применение нормального распределения в жизни
Закон нормального распределения
История применения закона нормального распределения
История ЗНР в социальных и биологических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появление первого ребёнка и т.д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые отклонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины».
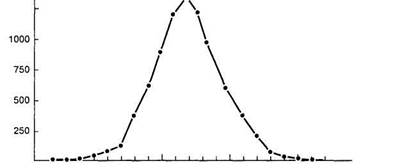
Рис. 1 Полигон частот для роста 8585 взрослых людей, родившихся в Англии в XIX веке (по Ф. Гальтону).
Эта формула и соответствующая ей кривая впоследствии получили название закона нормального распределения (ЗНР).
Таким образом, начиная со второй половины XIX века, измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа: если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует ЗНР. Это и есть закон нормального распределения.
ЗНР имеет целый ряд очень важных следствий. Одно из них состоит в том, что если при изучении некоторого свойства мы произвели его измерение на выборке испытуемых и получили отличающееся от нормального распределение, то это значит, что либо выборка нерепрезентативна генеральной совокупности, либо измерения произведены не в шкале равных интервалов.
НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ



Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.
История применения закона нормального распределения в социальных и биологических науках начинается, по-видимому, с работы бельгийского ученого А. Кетле «Опыт социальной физики» (1835 г.). В ней он доказывал, что такие явления, как продолжительность жизни, возраст вступления в брак и появления первого ребенка и т. д., подчиняются строгой закономерности. Она проявляется в том, что чаще всего встречаются средние значения соответствующих показателей, и чем больше отклонение от этой средней величины, тем реже встречаемость таких отклонений. Одинаковые отклонения от среднего в меньшую и в большую сторону встречаются одинаково реже, чем среднее значение. Эту закономерность он назвал «законом уклонения от средней величины». В его исследованиях, и позднее — в исследованиях англичанина Ф. Галь-тона, было доказано, что распределение частот встречаемости любого демографического (продолжительность жизни и пр.) или антропометрического (рост, вес и пр.) показателя, измеренного на большой выборке людей, имеет одну и ту же «колоколо-
152 165 178 191 РОСТ, CM
Рис. 5.1. Полигон частот для роста 8585 взрослых людей, родившихся в Англии в XIX в. 1

ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
 |
 |
образную» форму (см. рис. 5.1). Форма таких распределений может быть описана математической формулой, которую предложил еще в XVIII веке математик де Муавр.
где/(х,) — высота подъема кривой, е — основание натурального логарифма (примерно 2,718), л — число «пи» (примерно 3,14), Ми а — среднее и стандартное отклонения для переменной х„ которые определяют положение кривой на числовой оси и задают ее размах. Эта формула и соответствующая ей кривая (см. рис. 5.2) впоследствии получили название закона нормального распределения.
Итак, исход азартной игры, и продолжительность жизни, и рост человека — все это случайные события, частота (или вероятность) встречаемости которых подчинена закону нормального распределения. А. Кетле объяснял это существованием «идеала» человеческой природы, которому соответствуют средние значения различных пока-
Рис. 5.2. График распределения вероятностей выпадения «орлов» в игре с 10 подбрасываниями монеты и кривая нормального распределения
ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ
зателей. Ф. Гальтон, двоюродный брат Ч.Дарвина, проявление нормального закона рассматривал в связи с биологической изменчивостью, наследственностью и отбором. В дальнейшем трудами Ф. Гальтона и его последователей было доказано, что и психологические особенности, например способности, подчиняются нормальному закону. Поэтому дальнейшее развитие измерительного подхода в психологии и статистического аппарата проверки гипотез происходило на базе этого общего закона.
Подведем важный итог этого краткого исторического экскурса. Начиная со второй половины XIX столетия измерительные и вычислительные методы в психологии разрабатываются на основе следующего принципа. Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения. Это и есть закон нормального распределения.
Закон нормального распределения имеет целый ряд очень важных следствий, к которым мы не раз еще будем обращаться. Сейчас же отметим, что если при изучении некоторого свойства мы произвели его измерение на выборке испытуемых и получили отличающееся от нормального распределение, то это значит, что либо выборка нерепрезентативна генеральной совокупности, либо измерения произведены не в шкале равных интервалов.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК СТАНДАРТ
 |
 |
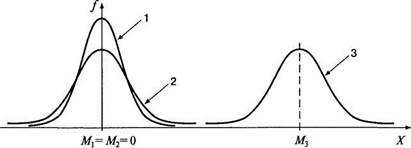
Каждому психологическому (или шире — биологическому) свойству соответствует свое распределение в генеральной совокупности. Чаще всего оно является нормальным и характеризуется своими параметрами: средним (М) и стандартным отклонением (о). Только эти два значения отличают друг от друга бесконечное множество нормальных кривых, одинаковой формы, заданной уравнением (5.1). Среднее задает положение кривой на числовой оси и выступает как некоторая исходная, нормативная величина измерения. Стандартное отклонение задает ширину этой кривой, зависит от единиц измерения и выступает как масштаб измерения (рис. 5.3).
ЧАСТЬ I. ОСНОВЫ ИЗМЕРЕНИЯ И КОЛИЧЕСТВЕННОГО ОПИСАНИЯ ДАННЫХ
Все многообразие нормальных распределений может быть сведено к одной кривой, если применить ^-преобразование (по формуле 4.8) ко всем возможным измерениям свойств. Тогда каждое свойство будет иметь среднее 0 и стандартное отклонение 1. На рис. 5.4 построен график нормального распределения для М= 0 и а = 1. Это и есть единичное нормальное распределение, которое используется как стандарт — эталон. Рассмотрим его важные свойства.
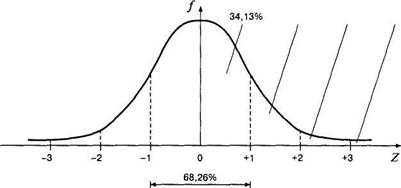 |
| 13,59% 2,14% 0,13% |


ГЛАВА 5. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ И ЕГО ПРИМЕНЕНИЕ
□ если х, имеет нормальное распределение со средним М и стандартным отклонением о, то z = (х— Мх)/а характеризуется единичным нормальным распределением со средним 0 и стандартным отклонением 1;
П площадь между х, и х2 в нормальном распределении со средним Мх и стандартным отклонением о равна площади между Z\ = (xl — Мх)/а и Z2 = (x2 — Мх)/а в единичном нормальном распределении.
Итак, наиболее важным общим свойством разных кривых нормального распределения является одинаковая доля площади под кривой между одними и теми же двумя значениями признака, выраженными в единицах стандартного отклонения.
Полезно помнить, что для любого нормального распределения существуют следующие соответствия между диапазонами значений и площадью под кривой:
М±а соответствует«68% (точно — 68,26%) площади;
М±2осоответствует =95% (точно — 95,44%) площади;
М±3а соответствует =100%(точно — 99,72%) площади.
Единичное нормальное распределение устанавливает четкую взаимосвязь стандартного отклонения и относительного количества случаев в генеральной совокупности для любого нормального распределения. Например, зная свойства единичного нормального распределения, мы можем ответить на следующие вопросы. Какая доля генеральной совокупности имеет выраженность свойства от — \о до +1о? Или какова вероятность того, что случайно выбранный представитель генеральной совокупности будет иметь выраженность свойства, на За превышающую среднее значение? В первом случае ответом будет 68,26% всей генеральной совокупности, так как от — 1 до +1 содержится 0,6826 площади единичного нормального распределения. Во втором случае ответ: (100-99,72)/2 = 0,14%.
Полезно знать, что если распределение является нормальным, то:
90%всех случаев располагается в диапазоне значений М+ 1,64а;
95%всех случаев располагается в диапазоне значений М± 1,96с;
99%всех случаев располагается в диапазоне значений М+ 2,58с.
Существует специальная таблица, позволяющая определять площадь под кривой справа от любого положительного z (приложение 1). Пользуясь ею, можно определить вероятность встречаемости значений признака из любого диапазона. Это широко используется при интерпретации данных тестирования.
Еще раз о нормальном распределении
После того, как Германия проиграла войну, экономическая ситуация в стране стала быстро ухудшаться. Все продукты были строго нормированы, а самый главный продукт питания, хлеб, выдавался из расчета 200 г. на душу населения в день. Все пекари получили строжайшую инструкцию изготовить специальные формы для выпечки 200-граммовых хлебцев — по 1 хлебцу в день на каждого из окрестных жителей.
Старый профессор Карл Z. каждое утро по дороге в университет заходил в булочную, чтобы купить дневную порцию хлеба. Однажды он заявил булочнику:
— Бесчестный вы человек! Вы обманываете своих покупателей! Ваши формы на 5% меньше, чем должны быть для выпечки 200-граммовых хлебцев, а сэкономленную муку вы продаете на черном рынке!
— Помилуйте, герр профессор! — возразил булочник. — Никто и никогда не выпекал хлебцы одного и того же размера. Одни хлебцы получаются на несколько процентов меньше нормы, другие — на несколько процентов больше.
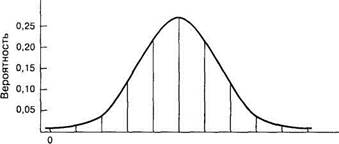
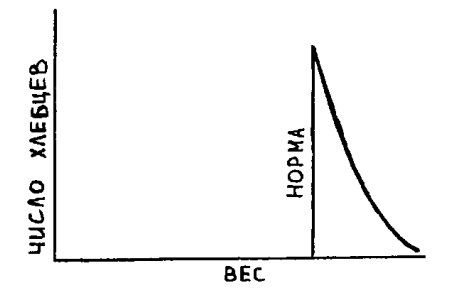
— Вот именно! — подтвердил профессор. — В течение нескольких месяцев я ежедневно взвешивал хлебцы, которые покупал у вас, на точных весах в моей лаборатории. Разумеется, результаты взвешивания дали естественный разброс. Вот график, на котором показано число хлебцев различного веса по сравнению с правильным весом (нормой).
Как видите, одни хлебцы весят всего 185 г, другие — целых 205 г, но средний вес (среднее арифметическое всех измерений) равен 195 г, вместо положенных 200 г. Вам нужно срочно изготовить новые формы для хлебцев правильных размеров, иначе я буду вынужден сообщить о вас властям.
— Разумеется, я изготовлю новые формы завтра же, герр профессор! — пообещал перепуганный булочник. — Смею заверить вас, что ошибка больше не повторится.
Через несколько месяцев профессор Z. снова обратился к булочнику.
— Я сообщил о вас властям сегодня, — сказал профессор. — Вы не изменили формы и продолжаете обманывать своих покупателей.
— Но герр профессор! — воскликнул булочник. — Уж теперь-то вы не можете обвинять меня в том, что я обманываю покупателей. Разве в хлебцах, которые вы покупали у меня за последние несколько месяцев, был недовес?
— Недовеса не было. Все хлебцы были весом в 200 г или тяжелее. Но объяснялось это не тем, что вы изготовили формы больших размеров, а тем, что отбирали для меня хлебцы покрупнее.
— Ну, этого вы никогда не сможете доказать! — презрительно процедил булочник.
— Еще как смогу! — возразил профессор Z. — Вот какое статистическое распределение я получил, взвешивая хлебцы, купленные у вас за последние несколько месяцев:
Вместо стандартного распределения ошибок, открытого великим немецкие математиком Карлом Фридрихом Гауссом, получилась сильно искаженная кривая, обрезанная слева и медленно спадающая справа. Статистические отклонения от среднего не могут привести к такому распределению. Ясно, что оно создано искусственно — тем, что вы отбирали для меня хлебцы весом от 200 г и более. Кривая, которую вы видите, — хвост гауссова распределения, т. е. того самого распределения, которое я получил, взвешивая хлебцы перед нашим первым разговором. Не сомневаюсь, что власти, отвечающие за распределение продуктов, прислушаются к моему сообщению.
И повернувшись на каблуках, профессор Z. вышел из булочной.
Гамов Г., Стерн М. Занимательная математика. — Ижевск: Научно-издательский центр «Регулярная и хаотическая динамика», 2001, стр. 62-64.
Новичкам. Опционы и Гауссово (нормальное) распределение.
Продолжаем грызть тему опционов по книгам Саймона и Натенберга, сегодня добрались до темы волатильность.
Волатильность — это то, что отличает торговлю фьючерсами от опционов. Кто не знает как работает волатильность, по каким законам она живет, не сможет работать с опционами. Там, где волатильность, там есть и теория вероятности, а там, где теория вероятности — сидит определенный математический аппарат.
Именно в этой точке гуманитарий опускает руки, потому что не может разобраться как работать с моделью Блэка-Шоулза, не знает элементарных понятий из теории вероятности, не знает как работает Гауссово распределение.
Будем двигаться понемногу, сегодня разберемся именно с Гауссовым распределением, я покажу на пальцах что это такое и уже потом будем постепенно углубляться в модель Блэка-Шоулза (да-да, уважаемые новички, без понимания как работает эта модель вы будете терять деньги на опционном рынке).
Что же такое Гауссово распределение, оно же распределение Гаусса-Лапласа? Это такое распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:
Важно знать следующие свойства функции плотности распределения Гаусса:
С вероятностью 68,2% случайная величина не отклонится от своего математического ожидания дальше, чем 1 сигма.
С вероятностью 95,4% случайная величина не отклонится от своего математического ожидания дальше, чем 2 сигма.
С вероятностью 99,7% случайная величина не отклонится от своего математического ожидания дальше, чем 3 сигма.
Что это такое и как с этим работать трейдеру?
Есть удивительный индикатор Боллинджера, который показывает среднюю, верхнюю и нижнюю границу диапазона изменения цены актива, по умолчанию там настроен параметр 2сигма. Таким образом, если бы рынок подчинялся распределению Гаусса, то с вероятностью 95,4% цена не должна выходить за границы диапазона. Но почему же иногда она выходит? Потому что нормальное распределение по Гауссу это всего лишь математическая модель, рынки же в основе своей живут не по распределению Гаусса, на рынках есть тренд и память. Именно поэтому о каком-то случайном блуждании цены говорить не приходится, но в то же время рынки очень часто живут также и по Гауссу, мы это видим во время боковиков, когда цена хаотично движется туда-сюда, но не выходит за границы диапазона. Это как раз частный случай хаотичного движения (пропал тренд).
Более простого изложения на практике «куполообразного» распределение вероятностей я нигде не видел ранее, именно этим меня и цепанула книга Натенберга. Респект автору, умеет он всё же нетривиальные вещи объяснить простым языком.
Случайное блуждание.
Возьмем для примера игру пинбол. Шарик катится вниз через частокол штырьков. Наткнувшись на штырек, он отклоняется вправо или влево с вероятностью 50%. После этого шарик попадает на новый уровень, где натыкается на другой штырек. Наконец, внизу он падает в одну из лунок.

Движение шарика через частокол штырьков называют случайным блужданием. Как только шарик попадает в этот частокол, никто не может повлиять на его траекторию, равно как и предсказать эту траекторию.
Если бросить достаточное количество шариков, то можно получить распределение, которое называется Гауссовым — большинство шариков попадает в центр игрового поля; чем дальше лунки расположены от центра, тем меньше шариков в них оказывается. Такое распределение называется еще нормальным или колоколообразным:

Если бросить бесконечно большое количество шариков, то распределение будет описываться колоколообразной кривой, изображенной на рисунке.
Низковолатильное распределение.
Теперь давайте слегка изменим условия игры, поставив вертикальные перегородки таким образом, что теперь, наткнувшись на штырек и отклонившись влево или вправо, шарик опустится до соприкосновения со следующим штырьком не на один, а на два уровня. Если бросить достаточное количество шариков, то получится распределение, представленное кривой на рисунке (низковолатильное распределение):

Поскольку боковые движения шариков ограничены, пик этой кривой будет выше, а ее хвосты будут более узкими, чем у кривой на предыдущем рисунке. Несмотря на изменения формы, это по-прежнему кривая нормального распределения, но с несколько иными характеристиками (для тех, кто владеет математическим аппаратом — параметр эксцесс отвечает за высоту пика).
Высоковолатильное распределение.
Наконец, мы можем поставить горизонтальные перегородки так, что, попадая на следующий уровень, шарик будет каждый раз отклоняться на два штырька влево или вправо. И снова, если бросить достаточное количество шариков, то получится распределение, представленное на рисунке:

У этой кривой, которая также отражает нормальное распределение вероятностей, пик намного ниже, а хвосты убывают намного медленнее, чем у кривых на предыдущих рисунках.
Для чего нам всё это нужно было?
Пусть боковые движения шарика символизируют повышательные и понижательные изменения цены базового актива, а движение вниз — течение времени. Если предположить, что цена Ri каждый день повышается или понижается на 2500 пунктов (шаг 1 страйка), то распределение значений цены через 15 дней будет представлено на рисунке с «колоколообразной» плотностью распределения вероятностей.
Если предположить, что цена Ri повышается на 2500 пунктов каждые 2 дня, то распределение будет похоже на рисунок «низковолатильного распределения».
А если предположить, что цена Ri за день растет или падает на 5000 пунктов (2 страйка), то распределение будет напоминать рисунок «высоковолатильного распределения».
Если сегодня Ri стоит 107 500, а срок действия опциона истекает через 15 дней, то как определить стоимость 112 500 колла?
Об этом в следующих сериях.
Если такие вот топики вам заходят — ставьте лайки, жмите колокольчик, пишите каменты.
Да сопутствует вам всем удача в опционном мире!
Применение нормального распределения в жизни
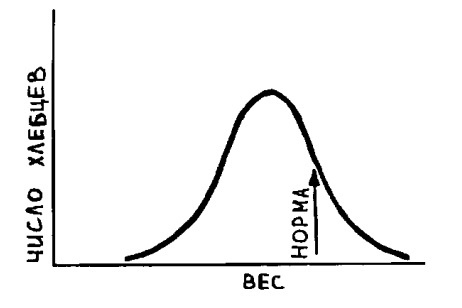
Закон нормального распределения, или как его еще называют – кривая Гаусса, является одним из основных столпов в теории вероятности. Его применение можно проследить практически во всех сферах современного человеческого знания, от физики до философии. Я же попробую в кратком обзоре на примерах, объяснить как можно применить этот принцип, при аналитике народных процессов в социологии.
Хотя точное вычисление кривой Гаусса и требует решения довольно сложного уравнения, в этом тексте знания высшей математики вам не потребуются. И так, давайте для начала поймем, в общих чертах, в чем смысл этого графика, на примере изображения, показанного в заголовке статьи. Закон нормального распределения показывает вероятность некоторого значения из некоторой градации этих самых значений. Ось X является цифровым представлением этой самой градации и уходит от нуля в обе стороны до относительной бесконечности (но в некоторых случая она жестка ограничена). Ось Y является показателем величины вероятности значения из градации и может быть от нуля до одного. Сложно? Нет, все просто, взгляните вот на этот график и вам станет все довольно ясно.
Допустим, вы идете по улице, хотите спросить что-то умное у прохожего, и обращаясь к случайному человеку, вы можете быть уверены в том, что с максимально вероятностью он будет человеком среднего ума, в меньшей вероятности, что он будет дураком или умником и в практически минимальной возможности – гением или откровенным тупицей.
Одним словом этот график показывает вероятностное распределение интеллектуальности общества. Таким образом, обратившись к любой позиции на графике, можно сказать, какова вероятность при переборе людей, встретить гения, умного или дурака.
Естественно этот график является просто примером, и может не иметь никакого отношения к реальности. Для реальной же картины подобного рода, должен работать целый статистический комитет. Как можно понять из приведенного примера, график может деформироваться, в ту или иную сторону, и представлять уже иную вероятность. Показанный же график, называется – Стандартным нормальным распределением, потому что такая форма кривой вероятности установлена самой природой. И если мы обратимся в мир биосферы, и будем оценивать разные вероятности, то обнаружим, что данная форма кривой будут доминировать.
В определении ЗНР я указал, что ось X уходит по обе стороны в бесконечность. Дело в том, что оценка, каких либо общественных величин методом живой статистики, является явлением, находящемся только в настоящем времени. Общество не стоит на месте, оно постоянно движется, развивается или деградирует, поэтому сейчас оно одно, завтра другое, а значит, будет и другая форма и положение кривой Гаусса. Если не уходить с позиции стандартного нормального распределения, то для демонстрации вышесказанного можно опереться на ту же кривую вероятности интеллектуальной развитости общества.
График представляет собой пример оценки интеллектуального развития общества за некоторый необъявленный промежуток времени. Зеленая кривая, находящаяся на нуле, показывает положение дел «раньше». Красная и синяя кривые показывают момент «сейчас». Две кривые (красная и синяя) показаны исключительно в качестве иллюстрации, так как в реальной ситуации будет только одна из них, ведь общество не может одновременно развиться и деградировать по одному и тому же критерию оценки. Разбор одной из кривых, например красной, покажет вот такую картину. Общество поумнело на две единицы градации, что стало причиной того, что те люди, которые раньше считались очень умными, стали обычным явлением, те, кого раньше считали гениями, стали частенько встречаться и уже не являются чем-то необычным, а не очень умные в былые времена люди стали считаться чуть ли не дегенератами. Полностью противоположная картина будет при оценке синей кривой. Ее кстати очень хорошо продемонстрировал фильм «Идиократия», в котором «человек со средним умом» попав в будущее, оказался умнейшим человеком на земле, потому что за столетия, общество умственно деградировало настолько, что уровень дегенерата в нем стал среднестатистическим.
На основе понимания и умения выстраивать эти графики, можно не только оценивать движение общества в прошлом, но и строить планы на будущее на основе осознания того, как должно быть. Например, усиленно рассматриваемую мной в последнее время проблему алкоголизации общества, можно привести вот в такой форме. (Это чисто мое субъективное мнение, сформированное не математической статистикой, а тем, что я лично вижу вокруг себя.)
В нормальном же обществе (зеленая кривая), трезвенник должен быть нормой. С минимальным отрывом от него должен идти идейный трезвенник. А вот равнодушный человек, позволяющий не отказаться от рюмочки, уходит в область рецидива, и становиться чуть ли не врагом общества. Пассивных алкоголиков как вы понимаете в том обществе вообще нет, так как они не смогут в нем существовать (они будут откровенными врагами народа, из-за того что понижают этику и демографию общества). Последнее как раз и выражено деформацией зеленой кривой Гаусса.
Ясное дело, что в этом крохотном тексте просто невозможно уложить всю полноту возможных вариантов применения закона нормального распределения в социологии. Но я надеюсь, что почву для размышлений я дал.
На мой взгляд, знанием данного закона, должен обладать любой человек, хотя бы чуть-чуть задумывающийся о своем будущем. А ведь, как известно – свое будущее, прямо зависит от будущего общества в целом, т. е. среды, в которой мы все живем. И если каждый будет знать, куда, а главное как нужно идти, то это уже гарантия уверенности, что мы идем к чему-то лучшему.
________________________________________ ________________________________________ ____