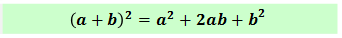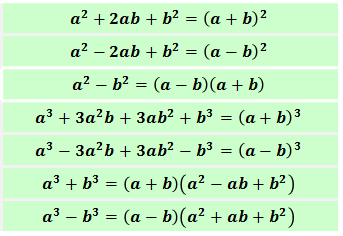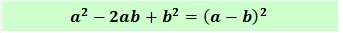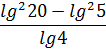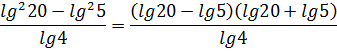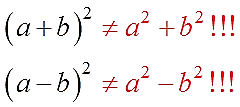применение формулы сокращенного умножения в жизни

Сокращенное умножение: правила, формулы

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Доказательство формул сокращенного умножения

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Как решаем:

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник

Формулы сокращённого умножения

Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…

Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…

Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов — что за звери?

Итак, вот они, формулы сокращённого умножения:

Эти семь формул — полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот — справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях — как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.

Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:

Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение — потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!

Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) — о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)

Зачем нужны формулы сокращённого умножения?

Полезная вещь первая — самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок — меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.

Сравним два равенства:

Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:

Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:

А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, — это разложение на множители! А разложение на множители — процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)

И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:

Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть — нет. Список, что приведён выше, — это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!

Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:

Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?

Запоминаем формулы сокращённого умножения! Секретные приёмы…

С выражениями (a+b) 3 и (a—b) 3 всё то же самое — куб суммы и куб разности соответственно.

Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?

А вот теперь начинается самое сложное — запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.

Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.

Итак, начинаем с квадрата суммы:

Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:

Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)

Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:

Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a 2 и b 2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.

В словесной расшифровке:

Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это — совсем другие формулы…

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Переходим к следующей группе формул — к сумме и разности кубов:

Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках — меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a 2 и b 2 — положительные!

Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!

Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках

часто называют неполным квадратом суммы/разности.

А теперь можно и шаблонные словесные формулировки из учебников привести:

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Остаётся последняя парочка — куб суммы и куб разности:

Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!

Итак, как запомнить куб суммы? Во-первых, все знаки в формуле — плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.

Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:

Такой порядок хорошо помогает не запутаться.)

Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b 2 ) даст плюс. И все дела.)

Разумеется, изложенные выше советы — это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)

Но, как ни крути, самый надёжный способ запомнить эти формулы — решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.

Ну что, потренируемся?)

Примеры на формулы сокращённого умножения.

Начнём с самого простого — с прямого применения формул. Для разминки.)

Преобразовать в многочлен:

Сразу видим квадрат скобок. А в скобках — сумму. Значит, работаем по самой первой формуле, вот этой:

Идём дальше: «Плюс удвоенное произведение первого выражения на второе…». Удвоенное — это умножение на двойку. Первое выражение — это 5x, второе — это 4y. Продолжаем:

Практически всё. Осталось «причесать» удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:

Это было разминочное задание. А теперь примерчик посерьёзнее.

Разложить на множители:

Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:

Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно — и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.

В нашем выражении есть x 2 и просто x. Ясное дело, отбрасываем все формулы с кубами — у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас — есть.

Остаются первые две формулы — квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы — только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула — это квадрат разности.

Но не факт, что квадрат разности сработает, совсем не факт… Наша задача — убедиться, что предложенное выражение 4x 2 –20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).

Для удобства я перепишу формулу и исходное выражение прямо одно под другим:

Всё? Можно записывать разложение? Пока нет.

Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.

Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:

Ура! Совпало! Значит, наше выражение — это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:

Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.

Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!

Например, такое задание:

Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…

Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos 2 x и sin 2 x. Удвоенное произведение, ясен перец, будет 2cos 2 x∙sin 2 x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:

А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!

Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.

В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:

А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.

Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…

Посему практический совет:

Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.

О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:

И запомните это крепко-накрепко!

Формулы — штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной — будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.

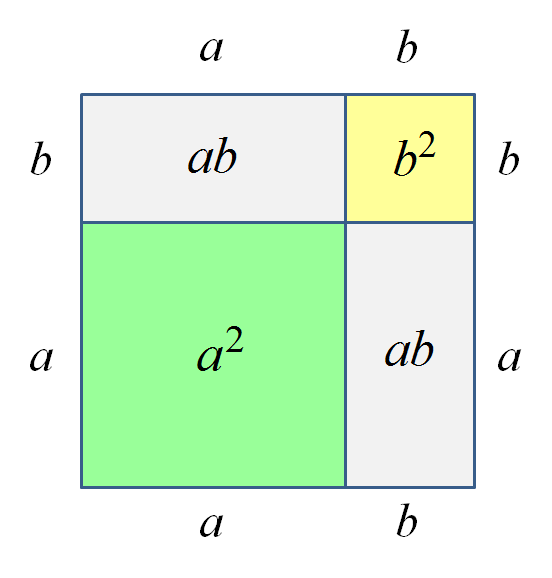
Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a — это 4 клетки, a b — это 2 клетки.

Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами — квадрат разности и разность квадратов. Попробуйте! Интересно.)

1. Преобразовать в многочлен стандартного вида:

Источник

Мастер-класс на тему «Применение формул сокращённого умножения»

Применение формул сокращённого умножения

Здравствуйте, уважаемые коллеги!

Я, Якубицкая Е.В., преподаю в школе предмет, который многие считают скучным, трудным и не нужным (математика).

— Математика-жизнь.- можно так сказать.

— Математика-жизнь?- можно так спросить.

— Математика-жизнь!- можно так воскликнуть.

А какой знак препинания поставите в конце данного предложения Вы, решите для себя сами. Что касается моего мнения, то всем своим ученикам я говорю словами Великого учёного М.В. Ломоносова: «Математику уже затем учить надо, что она ум в порядок приводит». (слайд 1,2)

Свой мастер-класс я посвятила теме, а вот какой…, назовём её после того, как проанализируем одну очень интересную загадку:

Задумайте число до 10

Умножьте его на себя

Прибавьте к результату задуманное число

К полученной сумме прибавьте 1

К полученному числу прибавьте задуманное число.

-Скажите мне, пожалуйста, число, которое у Вас получилось, и я отгадаю, какое число Вы задумали.

Решение: х 2 + х + 1 + х = х 2 + 2х + 1 = (х + 1) 2

Например: 5х5 + 5 + 1 + 5 = 36, тогда х = 36 – 1 = 6 – 1=5

Слайд 3 – тема мастер-класса.

Данная тема является очень актуальной для учителей математиков. При выполнении заданий ВПР, ОГЭ, ЕГЭ учащиеся порой не могут провести быстро свои расчёты в сложных примерах, а также не могут приводить многочлен к стандартному виду без раскрытия скобок и приведения подобных слагаемых.

Проанализировав проблему, я выявила причины, которые вызывают трудности при изучении данной темы:

Малое количество часов на отработку применения формул сокращённого умножения при большом объёме материала;

Отсутствие у обучающихся мотивации к данной теме;

Традиционный подход при изучении формул сокращённого умножения (механическое запоминание формул).

Исходя из этого, я предположила:

Если использовать необычные математические приёмы при изучении данной темы, то они помогут выявить интерес к формулам сокращённого умножения, а значит и их применению при решении заданий.

Цель и задачи моего мастер-класса представлены на слайде 4 :

Цель: представление наиболее результативных элементов собственной системы работы, методических приёмов, педагогических действий, обеспечивающих эффективное решение учебной задачи.

— Учить с увлечением помогут следующие методы урока по ФГОС:

Метод проблемного изложения;

Разноуровневый метод. (слайд 5)

А вот теперь, давайте с Вами, обратим внимание на традиционный вопрос ученика (просмотр видеофрагмента)

— Как мне могут пригодиться эти формулы сокращённого умножения? (ответы участников)

— Хороший вопрос… Вот тебе пример из жизни: у тебя есть квадратная комната 103 на 103 метра (хорошая комната, правда?) и необходимо застелить её плиткой метр на метр. Сколько нужно плиток? Продавец говорит, что тебе нужно около 12000 плиток. Проверять его расчёты тебе неловко, но ты можешь быстро посчитать в уме! Каким образом? ( ответы участников)

С помощью формул сокращённого умножения. Просто представь число 103, как сумму 100 и 3 и возведи её в квадрат:

103 2 = (100 + 3) 2 = 100 2 + 2х 100х3 + 3 2 = 10000+ 600+9= 10609

Тренировочный материал (слайд 6)

— Повторение формул сокращённого умножения можно провести так:

Источник

Формулы сокращённого умножения (ФСУ): таблица и применение

Одной из первых тем, изучаемых в курсе алгебры, являются формулы сокращённого умножения. В 7 классе они применяются в самых простых ситуациях, где требуется распознать в выражении одну из формул и выполнить разложение многочлена на множители или, наоборот, быстро возвести сумму или разность в квадрат или куб. В дальнейшем ФСУ используют для быстрого решения неравенств и уравнений и даже для вычисления некоторых числовых выражений без калькулятора.

Как выглядит список формул

Существует 7 основных формул, позволяющих быстро осуществить перемножение многочленов в скобках.

Иногда в этот список также включается разложение для четвёртой степени, которое следует из представленных тождеств и имеет вид:

Все равенства имеют пару (сумма — разность), кроме разности квадратов. Для суммы квадратов формула не приводится.

Остальные равенства легко запоминаются:

Следует помнить, что ФСУ работают в любом случае и для любых величин a и b: это могут быть как произвольные числа, так и целые выражения.

В ситуации, если вдруг не получается вспомнить, какой знак стоит в формуле перед тем или иным слагаемым, можно раскрыть скобки и получить тот же результат, что и после использования формулы. Например, если проблема возникла при применении ФСУ куба разности, нужно записать исходное выражение и поочерёдно выполнить умножение:

(a — b)³ = (a — b)(a — b)(a — b) = (a² ab — ab + b²)(a — b) = a³ a²b — a²b + ab² a²b + ab² + ab² b³ = a³ 3a²b + 3ab² b³.

В результате после приведения всех подобных членов был получен такой же многочлен, как и в таблице. Такие же манипуляции можно проводить и со всеми остальными ФСУ.

Применение ФСУ для решения уравнений

К примеру, нужно решить уравнение, содержащее многочлен 3 степени:

В школьной программе не рассматриваются универсальные приёмы для решения кубических уравнений, и подобные задания чаще всего решаются более простыми методами (например, разложением на множители). Если заметить, что левая часть тождества напоминает куб суммы, то уравнение можно записать в более простом виде:

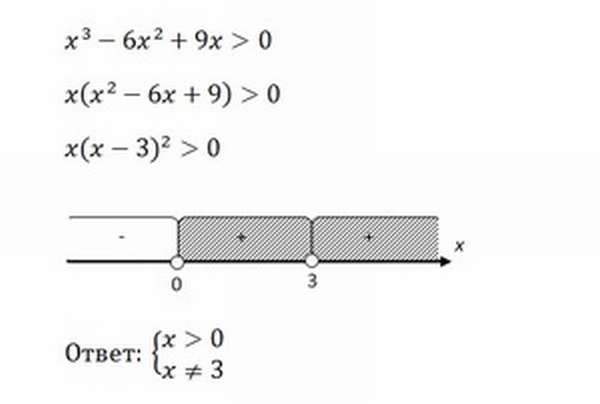
Аналогичным способом решаются неравенства. Для примера можно решить неравенство x³ 6x² + 9x &gt, 0.

В первую очередь необходимо разложить выражение на множители. Вначале нужно вынести за скобку x. После этого следует обратить внимание, что выражение в скобках можно преобразовать в квадрат разности.

Затем необходимо найти точки, в которых выражение принимает нулевые значения, и отметить их на числовой прямой. В конкретном случае это будут 0 и 3. Затем методом интервалов определить, в каких промежутках x будет соответствовать условию неравенства.

ФСУ могут оказаться полезными при выполнении некоторых расчётов без помощи калькулятора:

703² 203² = (703 + 203)(703 — 203) = 906 ∙ 500 = 453000.

Кроме того, раскладывая выражения на множители, можно легко выполнять сокращение дробей и упрощение различных алгебраических выражений.

Примеры задач для 7−8 класса

В заключение разберём и решим два задания на применение формул сокращённого умножения по алгебре. Если вы новичек, то лучше всего начать играть без настоящих ставок. Однако если уже вы решились, то найти интернет казино вулкан с выводом на реальные деньги можно с помощью рейтингов или же обратившись за советом к более опытным гемблерам. В принципе можно попробовать метод проб и ошибок, но это будет сложнее и дольше.

Задача 1. Упростить выражение:

(m + 3)² + (3m + 1)(3m — 1) — 2m (5m + 3).

Решение. В условии задания требуется упростить выражение, т. е. раскрыть скобки, выполнить действия умножения и возведения в степень, а также привести все подобные слагаемые. Условно разделим выражение на три части (по числу слагаемых) и поочерёдно раскроем скобки, применяя ФСУ там, где это возможно.

Подставим полученные результаты в исходное выражение:

(m² + 6m + 9) + (9m² 1) — (10m² + 6m).

С учётом знаков раскроем скобки и приведём подобные слагаемые:

m² + 6m + 9 + 9m² 1 — 10m² 6m = 8.

Задача 2. Решить уравнение, содержащее неизвестное k в 5 степени:

k⁵ + 4k⁴ + 4k³ 4k² 4k = k³.

Решение. В этом случае необходимо воспользоваться ФСУ и методом группировки. Нужно перенести последнее и предпоследнее слагаемое в правую часть тождества.

k⁵ + 4k⁴ + 4k³ = k³ + 4k² + 4k.

Из правой и из левой части выносится общий множитель (k² + 4k +4):

k³(k² + 4k + 4) = k (k² + 4k + 4).

Всё переносится в левую часть уравнения, чтобы в правой остался 0:

k³(k² + 4k + 4) — k (k² + 4k + 4) = 0.

Снова необходимо вынести общий множитель:

Из первого полученного сомножителя можно вынести k. По формуле краткого умножения второй множитель будет тождественно равен (k + 2)²:

Использование формулы разности квадратов:

Поскольку произведение равно 0, если хотя бы один из его множителей нулевой, найти все корни уравнения не составит труда:

На основании наглядных примеров можно понять, как запомнить формулы, их отличия, а также решить несколько практических задач с применением ФСУ. Задачи простые, и при их выполнении не должно возникнуть никаких сложностей.

Источник