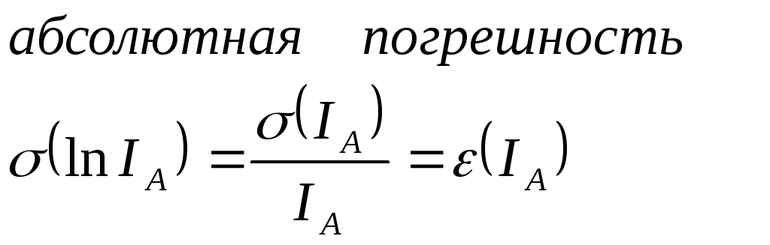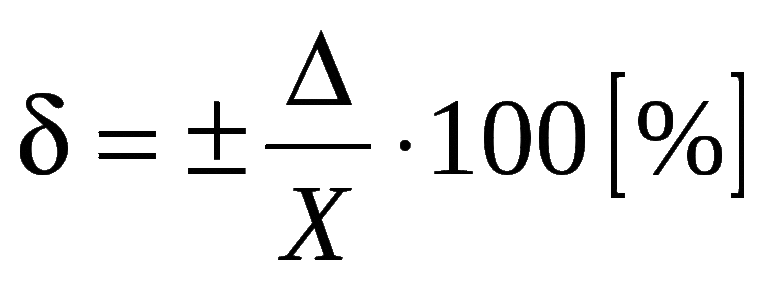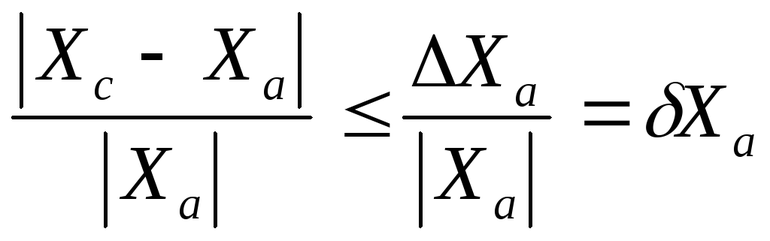погрешность это в жизни

ПОГРЕШНОСТЬ

Полезное

Смотреть что такое «ПОГРЕШНОСТЬ» в других словарях:

погрешность — См. ошибка. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. погрешность заблуждение, ошибка; грубая ошибка, промах, отклонение; ляпсус, ошибочка, упущение, накладка, оплошность,… … Словарь синонимов

ПОГРЕШНОСТЬ — ПОГРЕШНОСТЬ, погрешности, жен. Ошибка, неправильность, неточность или промах в каком нибудь деле. Ряд погрешностей в выводах. || Неправильность, неточность в работе какого нибудь механизма. Погрешность в часах. || Разность между истинной… … Толковый словарь Ушакова

ПОГРЕШНОСТЬ — (1) вычислений (см.), характеризующая степень близости точных и приближённых значений рассматриваемых величин, выражается в разности между истинным и приближённым значением искомой величины. В приближённых вычислениях применяют величины: а)… … Большая политехническая энциклопедия

ПОГРЕШНОСТЬ — Разность х а, где а данное число, которое рассматривается как приближенное значение некоторой величины, точное значение которой равно х. Разность х а называется также абсолютной погрешностью. Отношение х а к а называется относительной… … Большой Энциклопедический словарь

ПОГРЕШНОСТЬ — ПОГРЕШНОСТЬ, и, жен. Ошибка, промах. П. в расчётах. Допустить п. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

погрешность — Отклонение значения измеренной или вычисленной величины от действительного её значения ввиду неточности измерений или вычислений [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики метрология, основные… … Справочник технического переводчика

Погрешность — – отклонение значения измеренной или вычисленной величины от действи­тельного её значения ввиду неточности измерений или вычислений. [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Рубрика термина: Общие… … Энциклопедия терминов, определений и пояснений строительных материалов

Погрешность — 10. Погрешность По title= РМГ 29 99 ГСИ. Метрология. Основные термины и определения Источник: ГОСТ 12.1.016 79: Система станд … Словарь-справочник терминов нормативно-технической документации

Погрешность — измерения оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины… … Википедия

Погрешность СИ — 4. Погрешность СИ метрологическая характеристика СИ, определяемая как отличие показания СИ (X) от истинного значения (Х0) измеряемой величины, в качестве которого принимается значение величины, воспроизводимой соответствующим эталоном: абсолютная … Словарь-справочник терминов нормативно-технической документации

ПОГРЕШНОСТЬ — разность х а, где а данное число, к рое рассматривается как приближенное значение нек рой величины, точное значение к рой равно х. Разность х а наз. также абсолютной П. Отношение х а к а наз. относительной П. числа а. Для характеристики П. обычно … Математическая энциклопедия

Источник

Чтобы оценить степень отклонения, используется показатель абсолютной и относительной погрешности.

В математике, физике и метрологии этот коэффициент может быть использован для округления полученных результатов.

Показатель бывает нескольких видов. Для его определения применяют разные методы.

Понятие и классификация

Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.

Существует несколько разновидностей погрешности:

Выделяют также отклонения прямых или косвенных измерений. Вторая разновидность учитывается в тех случаях, когда измерить величину напрямую невозможно и ее можно посчитать по формулам исходя из других данных.

Абсолютная и относительная погрешности

Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.

Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г

Для вычислений разработана специальная формула: Δа=А-а,

где А — это точная величина,

а — приближенная, это число, которое немного отличается от точного.

Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.

Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.

Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.

Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.

Методики расчета

Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

Для определения предельного отклонения выбирают наибольшее значение из всех полученных.

Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:

Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение. При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.

При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.

Произвести необходимые расчеты можно с помощью онлайн-калькулятора. В окошки вносятся необходимые данные, после чего программа выдает результат.

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

Эти показатели вычисляются на основе доверительной вероятности и большого количества измерений.

Источник

Погрешность

Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.

Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».

Содержание

Определение погрешности

В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.

Классификация погрешностей

По форме представления

где X_true — истинное значение, а X_meas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина X_meas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.

,

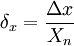
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то X_n определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.

По причине возникновения

В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.

Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.

Источник

Погрешность

Чтобы качественно проводить маркетинговые исследования, необходимо учитывать погрешность измерений. Из-за пренебрежения этим параметром рекламная кампания может не пройти успешно и принести убытки фирме. Производя математические расчеты, удается получить данные, максимально приближенные к реальным цифрам.

Определение

Проводя измерение параметров рынка, маркетолог получает результаты в виде таблиц, графиков и пр. Эти данные он предоставляет заказчику. Но в отчетах не все специалисты указывают важную величину — погрешность, о которой клиент не подозревает.

Погрешность — это отклонение результата данных от измеряемой величины. Термин используется в физике, экономике и маркетинге.

Погрешность измерений — это сумма всех погрешностей, у каждой из которых имеется причина.

Оценка специалиста считается неточной, если эта величина не указана.

Что влияет на погрешность

На погрешность влияют:

неточности из-за принципа регистрации;

причины, объясняемые концевой мерой;

факторы, обусловленные исполнителем действий;

причины, провоцируемые изменениями условий.

Погрешность, связанная с методиками измерения (их несовершенство, упрощение) возникает из-за выбора примерных формул или неподходящего способа. Использование не того метода случается из-за несоответствия рассматриваемой величины и модели.

Факторы, влияющие на процесс:

Вариативность показаний — это самая явная разность показателей, полученных в прямом или обратном ходе при одинаковом действительном значении рассматриваемой величины и неизменных окружающих условий процесса.

Прецизионность — позволяет понять, насколько точно производятся расчеты. Определяется тем, насколько схожие получается показатели при одинаковых условиях измерений.

Классификация

Погрешности классифицируются по нескольким характеристикам. В маркетинговых исследованиях используются не все ее виды, поскольку погрешность в этой сфере не измеряется при помощи специальных приборов.

По форме представления

Первый тип — абсолютная погрешность. Она представляет собой алгебраическую разность между реальным и номинальными значениями. Она регистрируется в тех же величинах, что и основной объект. В расчетах абсолютный показатель помечается буквой ∆.

Например, линейка — наиболее простой и привычный каждому измерительный инструмент. При помощи верхней шкалы на ней определяются значения с точностью до миллиметра. Нижняя имеет другой масштаб (до 0,1 дюйма–2,54 мм). Несложно проверить, что на этом приборе погрешность верхней части меньше, чем нижней. Точность измерений в случае с линейкой будет зависеть от ее конструктивных особенностей.

Абсолютная погрешность измеряется той же единицей измерений, что и изучаемая величина. В процессе используется формула:

Δ = х1 – х2, где х1 — измеренная величина, а х2 — реальная величина.

Второй тип – относительная погрешность (проявляется в виде отношение абсолютного и истинного значения). Показатель не имеет собственной единица измерения или отражается процентно. В расчетах помечается как δ.

Она является более сложным значением, чем может показаться. В расчетах используется формула:

Стоит отметить, что если истинное значение имеет малую величину, то относительная — большую. Например, если стандартной линейкой (30 см) измеряется коробки (150 мм), то вычисление будет иметь вид: δ = 1 мм/150 мм = 0,66%. Если этот же прибор использовать для экрана смартфона (80 мм), то получится δ = 1 мм/80 мм = 1,25%. Получается, что в обоих случаях абсолютная погрешность не изменяется, но относительная отличается в разы. Во втором случае рекомендуется использовать более точный прибор.

Последний тип — приведенная погрешность. Она используется, чтобы не допустить такого разброса на одном приборе. Работает, как относительная, но вместо истинного значения в формуле применяется нормирующая шкала (общая длина линейки, например).

γ = (Δ / х3)·100 %, где х3 — это нормирующая шкала

Например, если потребуется измерить ту же коробку и смартфон, то придется учесть абсолютную величину в 1мм и приведенную погрешность — 1/300*100 =0,33 %. Если взять швейный метр и сравнить его с линейкой, то получится, что первый показатель в обоих случаях остается 1 мм, а второй отличается в разы (0,33% и 0,1%).

По причине возникновения

Тут выделяются два типа погрешностей:

Инструментальные — они объясняются особенностями строения измерительных приборов. Могут встречаться на фоне недостаточного качества частей оборудования. К такого рода погрешностям относят производство конструкции, ошибки из-за трения механизмов, малой жесткости поверхностей. Показатель отличается для любого из измерений и не может быть обобщен.

Методическая — это неточности расчетов, проявляющиеся из-за несовершенства применяемых методом, ошибок вычислений, соотношений, применяемых для оценки.

В маркетинге возможен только второй тип погрешности.

По характеру проявления

Выделяются систематические погрешности, которые характеризуются постоянными или закономерными изменениями показателей при повторных измерениях в пределах одной величины.

Другой вид — случайные погрешности. Они проявляются в произвольном порядке при повторном измерении одних и тех же величин.

Статическая погрешность — это неточность результата, характерная для статических измерений.

Динамическая погрешность — характерна для изменяемых величин.

По способу измерения

Выделяется погрешность градуировки приборов. Относится к действительному значению величины, указанному в той или другой отметке прибора в результате нанесения градуировки.

Также встречается неточность адекватности модели. Проявляется в виде неточности при подборе функциональной зависимости. В качестве примера можно взять процесс расчета линейной зависимости по сведениям, которые эффективнее отражаются совсем другим методом. Эта неточность используется для проверки модели.

Заключение

В маркетинге обычно используют данные статистической погрешности. Они помогают специалистам предварительно узнать результат и определить успешность рекламной кампании. Знание формул и умение проводить расчеты повышает экспертность и ценность специалиста.

Источник

Погрешности экспериментальных результатов

Какие бывают погрешности

Любое число, которое выдает нам эксперимент, это результат измерения. Измерение производится прибором, и это либо непосредственные показания прибора, либо результат обработки этих показаний. И в том, и в другом случае полученный результат измерения неидеален, он содержит погрешности. И потому любой грамотный физик должен не только предъявить численный результат измерения, но и обязан указать все сопутствующие погрешности. Не будет преувеличением сказать, что численный экспериментальный результат, предъявленный без указания каких-либо погрешностей, бессмыслен.

В физике элементарных частиц к указанию погрешностей относятся исключительно ответственно. Экспериментаторы не только сообщают погрешности, но и разделяют их на разные группы. Три основных погрешности, которые встречаются чаще всего, это статистическая, систематическая и теоретическая (или модельная) погрешности. Цель такого разделения — дать четкое понимание того, что именно ограничивает точность этого конкретного измерения, а значит, за счет чего эту точность можно улучшить в будущем.

Статистическая погрешность связана с разбросом значений, которые выдает эксперимент после каждой попытки измерить величину.

Систематическая погрешность характеризует несовершенство самого измерительного инструмента или методики обработки данных, а точнее, недостаточное знание того, насколько «сбоит» инструмент или методика.

Теоретическая/модельная погрешность — это неопределенность результата измерения, которая возникла потому, что методика обработки данных была сложная и в чем-то опиралась на теоретические предположения или результаты моделирования, которые тоже несовершенны. Впрочем, иногда эту погрешность считают просто разновидностью систематических погрешностей.

Наконец, в отдельный класс, видимо, можно отнести возможные человеческие ошибки, прежде всего психологического свойства (предвзятость при анализе данных, ленность при проверке того, как результаты зависят от методики анализа). Строго говоря, они не являются погрешностью измерения, поскольку могут и должны быть устранены. Зачастую это избавление от человеческих ошибок может быть вполне формализовано. Так называемый дважды слепой эксперимент в биомедицинских науках — один тому пример. В физике частиц есть похожие приемы (см. заметку Что означает «слепой анализ» при поиске новых частиц?).

Что означает погрешность

Стандартный вид записи измеренной величины с погрешностью знаком всем. Например, результат взвешивания какого-то предмета может быть 100 ± 5 грамм. Это означает, что мы не знаем абсолютно точно массу, она может быть и 101 грамм, и 96 грамм, а может быть и все 108 грамм. Но уж точно не 60 и не 160 грамм. Мы говорим лишь, сколько нам показывают весы, и из каких-то соображений определяем тот примерный разброс, который измерение вполне могло бы дать.

Тут надо подчеркнуть две вещи. Во-первых, в бытовой ситуации значение 100 ± 5 грамм часто интерпретируется так, словно истинная масса гарантированно лежит в этом диапазоне и ни в коей мере не может быть 94 или 106 грамм. Научная запись подразумевает не это. Она означает, что истинная масса скорее всего лежит в этом интервале, но в принципе может случиться и так, что она немножко выходит за его пределы. Это становится наиболее четко, когда речь идет о статистических погрешностях; см. подробности на страничке Что такое «сигма»?.

Во-вторых, надо четко понимать, что погрешности — это не ошибки эксперимента. Наоборот, они являются показателем качества эксперимента. Погрешности характеризуют объективный уровень несовершенства прибора или неидеальности методики обработки. Их нельзя полностью устранить, но зато можно сказать, в каких рамках результату можно доверять.

Некоторые дополнительные тонкости, связанные с тем, что именно означают погрешности, описаны на странице Тонкости анализа данных.

Как записывают погрешности

Указанный выше способ записи не уточняет, что это за погрешность перед нами. В физике элементарных частиц при предъявлении результатов источники погрешностей принято уточнять. В результате запись результата может иногда принять пугающий своей сложностью вид. Таких выражений не надо бояться, просто нужно внимательно посмотреть, что там указано.

В самом простом случае экспериментально измеренное число записывается так: результат и две погрешности одна за другой:

Тут вначале всегда идет статистическая, а за ней — систематическая погрешность. Если же измерение не прямое, а в чем-то опирается на теорию, которая тоже не идеально точна, то следом за ними приписывается теоретическая погрешность, например:

μ = 1,33 ± 0,14 ± 0,15 ± 0,11.

Иногда для пущей понятности явно указывают, что есть что, и тогда погрешностей может быть даже больше. Это делается вовсе не для того, чтобы запутать читателя, а с простой целью: упростить в будущем расчет уточенного результата, если какой-то один из источников погрешностей будет уменьшен. Вот пример из статьи arXiv:1205.0934 коллаборации LHCb:

Нередки также случаи, когда погрешности в сторону увеличения и уменьшения разные. Тогда это тоже указывается явно (пример из статьи hep-ex/0403004):

И наконец, совсем экзотический случай: когда величина настолько плохо определена, что погрешность пишут не к самому числу, а к показателю степени. Например, 10 12 ± 2 означает, что величина вполне может лежать где-то между 10 миллиардами и 100 триллионами. В этом случае обычно нет большого смысла разделять погрешности на разные типы.

Величина со всеми явно указанными погрешностями часто не очень удобна для работы, например при сравнении теории и эксперимента. В этом случае погрешности суммируют. Эти слова ни в коем случае нельзя воспринимать как простое сложение! Как правило, речь идет о сложении в квадратах: если все три типа погрешностей обозначить как Δx_stat., Δx_sys., Δx_theor., то глобальная погрешность обычно вычисляется по формуле

Стоит еще добавить, что в других разделах физики нередко используют иную запись: вместо символа «±» погрешность просто помещают в скобках. Тогда ее понимают так: это погрешность, выраженная в единицах последней значащей цифры. Например, 100(5) означает 100 ± 5, а 1,230(15) означает 1,230 ± 0,015. В этом случае принципиально важно писать правильное число нулей в результате измерения, ведь запись 1,23(15) уже будет означать вдесятеро большую погрешность: 1,23 ± 0,15.

Как изображают погрешности

Когда экспериментально измеренные значения наносятся на график, погрешности тоже приходится указывать. Это обычно делают в виде «усов», как на рисунке слева. Такие «усы» с засечками относятся к глобальной погрешности. Если же хочется разделить статистические и систематические погрешности, то делают так, как показано на рисунке справа. Здесь засечки показывают только статистические погрешности, а полные усы во всю длину отвечают глобальным погрешностям. Другой вариант: выделение полных погрешностей цветом, как это показано, например, на рисунке с данными ATLAS по хиггсовскому бозону.

Наконец, когда экспериментальная точка имеет отдельные погрешности по обеим осям, то их тоже наносят, и результат выглядит в виде крестика.

Источник