подобные треугольники в жизни

Проект по математике «Практическое применение подобия треугольников «

МБОУ СОШ № 4 им. Г.К. Жукова

Исследовательская работа по геометрии

Шильдкравт Екатерина Викторовна

Комаров Даниил Николаевич

г.о. Краснознаменск Московской области, 2019-2020 учебный год

Глава 1. Обзор литературы.

1.1. Историческая справка …………………………………………………3

1.2. Основные определения и понятия подобия треугольников..…… ….4

Глава 2. Измерение высоты объекта

2.4. Практическая часть ………………………………….…… …. 9

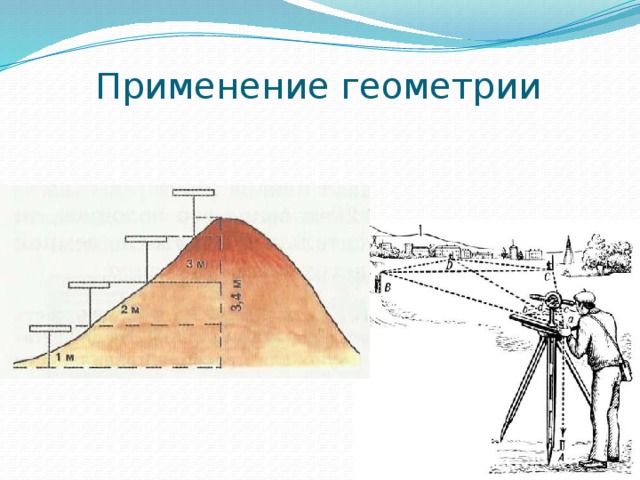
. Вернемся к началу прошлого столетия. Великий французский архитектор Корбюзье как-то воскликнул: «Всё вокруг геометрия!». Сегодня уже в начале 21-го столетия мы можем повторить это восклицание с еще большим изумлением. В самом деле, посмотрите вокруг — всюду геометрия! Современные здания и космические станции, авиалайнеры и подводные лодки, интерьеры квартир и бытовая техника, микросхемы и даже рекламные ролики. Воистину, современная цивилизация — это Цивилизация Геометрии. Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых.

Если человек знает признаки подобия треугольников, возникает ли необходимость их применять в жизни?

Найти области применения подобия треугольников в жизни человека.

изучить литературу по данной теме;

изучить историю возникновения понятия подобия;

узнать, где применяется подобие треугольников;

измерить высоту объекта при помощи подобия треугольников одним из способов.

поиск, анализ, математическое моделирование.

Обратимся к Википедии.

Геоме́трия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают написанные в III веке до н. э. «Начала» Евклида.

Геометрия греков, называемая сегодня евклидовой или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием.

Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.

Пропорциональность отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна ещё вавилонским ученым, хотя некоторые приписывают это открытие Фалесу Милетскому.

По преданию, Фалес измерил высоту египетской пирамиды (предположительно пирамиды Хеопса), применив геометрическую теорему, носящую его имя, — теорему Фалеса.

Дело было так. Фараон привез Фалеса к пирамидам и, желая испытать его, предложил измерить их высоту. Ученый принял вызов. Он воткнул в землю палку, дождался, когда длина тени от палки стала равной ее высоте, и повелел измерить тень от пирамиды, заявив, что высота тени в этот момент равна высоте самой пирамиды.

1.2. Основные определения и понятия подобия треугольников.

В жизни мы встречаемся не только с равными фигурами, но и с такими, которые имеют одинаковую форму, но разные размеры. Геометрия называет такие фигуры подобны.

Некоторые думают, что подобными могут быть только треугольники, но на самом деле совершенно произвольные фигуры могут быть подобны. Подобными могут являться пятиугольники, фигуры-звёзды, фигуры-стрелки, параллелограммы, многоугольники.

У всех подобных фигур одинаковые формы, но разные размеры.

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Свойства подобных треугольников:

Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.

Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.

Признаки подобия треугольников :

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Глава 2. Измерение высоты объекта

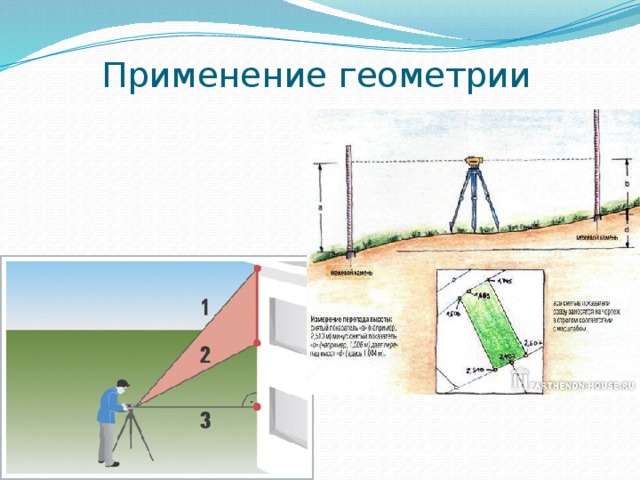
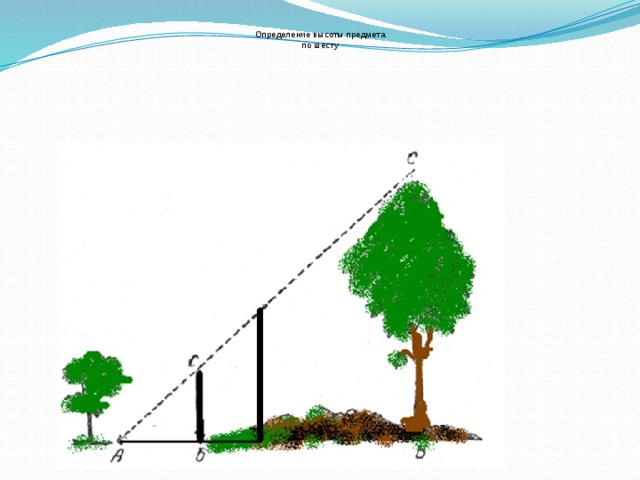
В основе этого метода лежит видоизмененный способ Фалеса, позволяющий использовать тень любой длины. Для измерения высоты объекта необходимо на некотором отдалении от дерева воткнуть в землю шест.

По данным с рисунка мы можем рассчитать высоту статуи:

500 мм х 4000 мм : 350 мм = 5 714 мм или 5 метров 71 см

Ответ: высота статуи 5 м 71 см

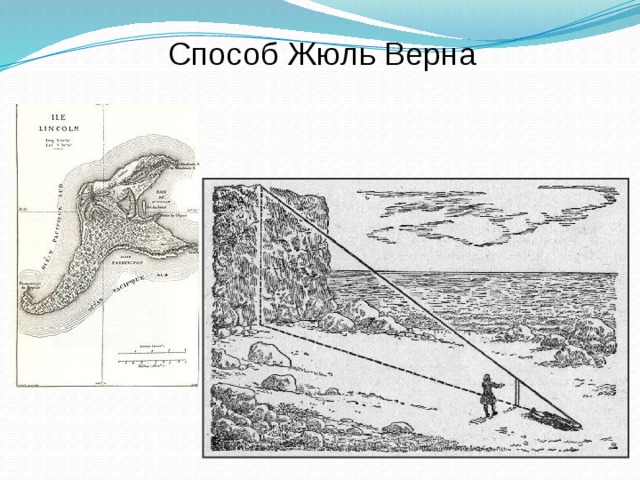
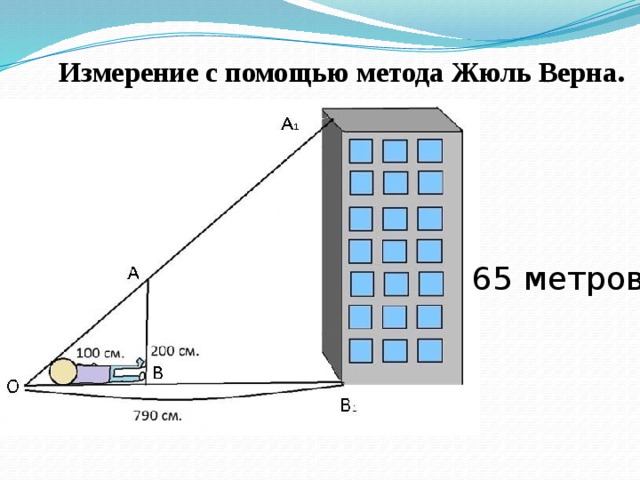
Этот метод был подробно описан в известном, захватывающем, приключенческом романе Жюль Верна «Таинственный остров». Шест длиной приблизительно равный росту человека втыкается в землю отвесно. Место для шеста надо выбрать так, чтобы человек, лежащий на земле, видел верхушку дерева на одной прямой с верхней точкой шеста. Недостаток этого метода состоит в том, что нельзя производить измерения в плохую погоду, т.к. необходимо ложиться на землю и можно испачкаться.

Расчет по данному методу я буду делать в практической части работы.

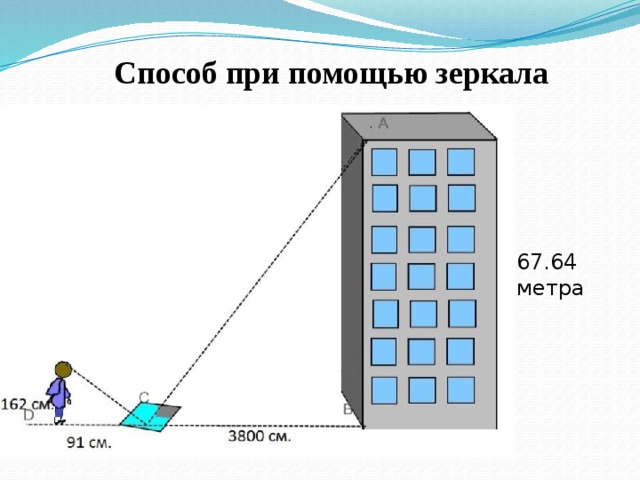
2.3 С помощью зеркала

На некотором расстоянии от дерева на ровной земле кладётся зеркало, и отходят от него назад в такую точку, стоя в которой наблюдатель видит верхушку дерева.

2.4 Практическая часть

Для проведения собственных измерений я решил взять метод с помощью шеста. Во втором случае, будем измерять расстояние до выбранного объекта, зная его высоту.

Все измерения мне помогала проводить мама.

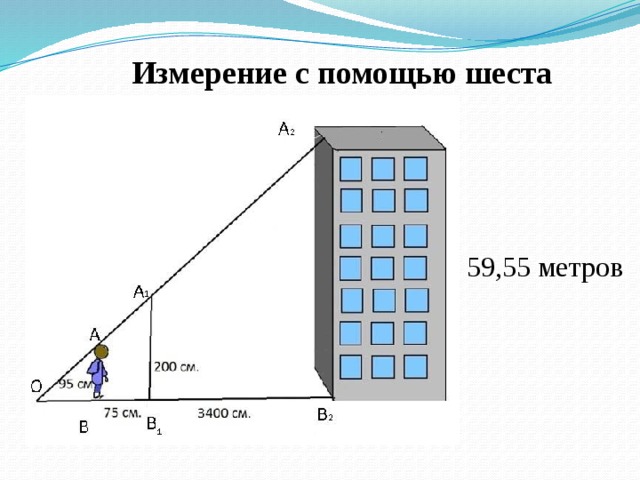
2.4.1 Измерения при помощи шеста

EB – расстояние от шеста до лежащего человека.

∆ АВС подобен ∆DBE т. к. ∟C = ∟E (соответственные), ∟B – общий =>

Высота ели равна 10,33 м.

2.4.2 Измерения расстояния до недоступной точки.

Мы взяли то же самое дерево и удалились от него на такое расстояние, чтобы длина большого пальца издалека была равна высоте дерева.

Вот, что у нас получилось.

Длина пальца – 0,07 м

Расстояние от глаза до пальца – 0,55 м

Изучение темы обогатили меня новыми знаниями, расширили кругозор по геометрии. Мною были изучены различные способы измерения высоты предмета. Полученные знания достаточно легко применяются на практике. Высоту столба, дерева можно измерить разными способами: с помощью лужи, зеркала, используя шест, и специальные приспособления. Исследованные мною методы дают результаты с минимальной погрешностью.

Можно сделать выводы :

1. Применение подобия треугольников незаменимы в нахождении высоты объекта.

2. Результаты исследования получаются более точные, если мы более точно измеряем расстояние до объекта.

3. Существует большое количество способов измерения высоты объекта.

Геометрические знания и умения, геометрическая культура и развитие являются сегодня профессионально значимыми для многих современных специальностей, для дизайнеров и конструкторов, для рабочих и ученых и многих других профессий. Знания, полученные в ходе исследовательской работы, останутся в моей памяти надолго, и я теперь с легкостью могу применять их на практике.

Источник

Применение подобия треугольников на практике

Применение подобия треугольников на практике

Содержимое разработки

Проект «Применение подобия треугольников на практике»

1. Пояснительная записка

2. Исследовательская работа

4. Видеоинтервью (требуется интернет)

Проект «Применение подобия треугольников на практике»

Учитель математики Максимов Ф.А.

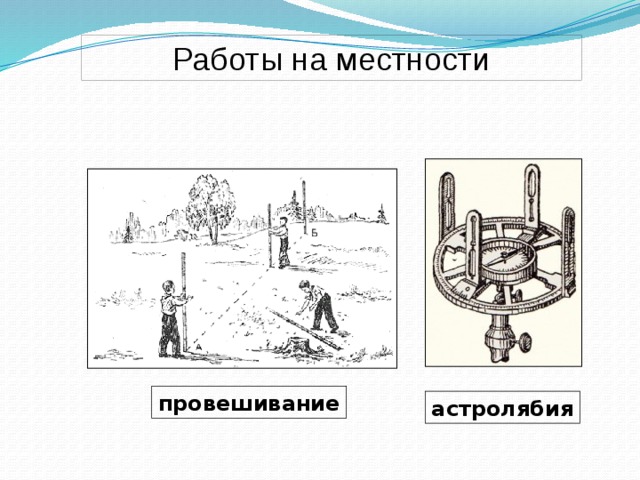
Работы на местности

Определение высоты пирамиды

Определение высоты предмета

Определение высоты предмета

(фр. L’Île mystérieuse ) —

впервые опубликованный в

1874 году. Является

произведений Верна «20000

лье под водой» и «Дети

капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.

Определение высоты предмета

Определение высоты предмета

Определение высоты предмета

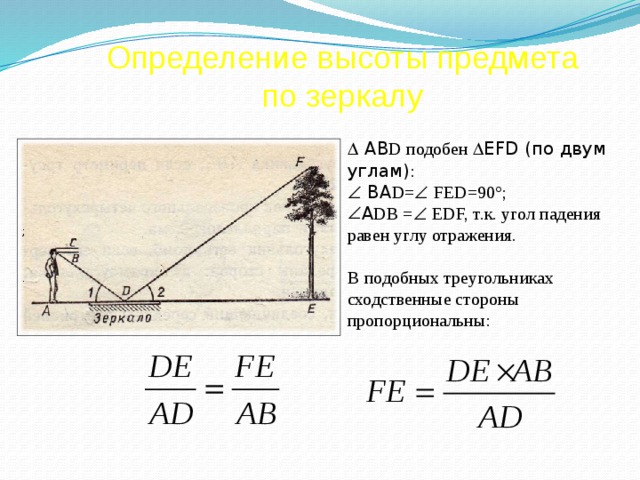
 АВ D подобен  EFD (по двум углам) :

В подобных треугольниках сходственные стороны пропорциональны:

до недоступной точки.

до недоступной точки.

до недоступной точки.

до недоступной точки.

до недоступной точки.

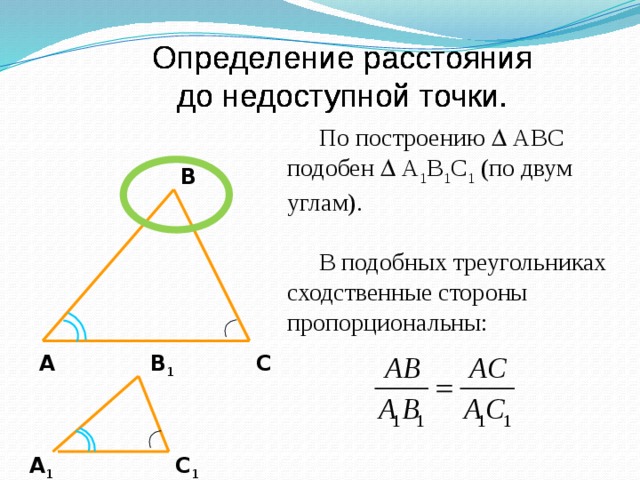
По построению  АВС подобен  А 1 В 1 С 1 (по двум углам).

В подобных треугольниках сходственные стороны пропорциональны:

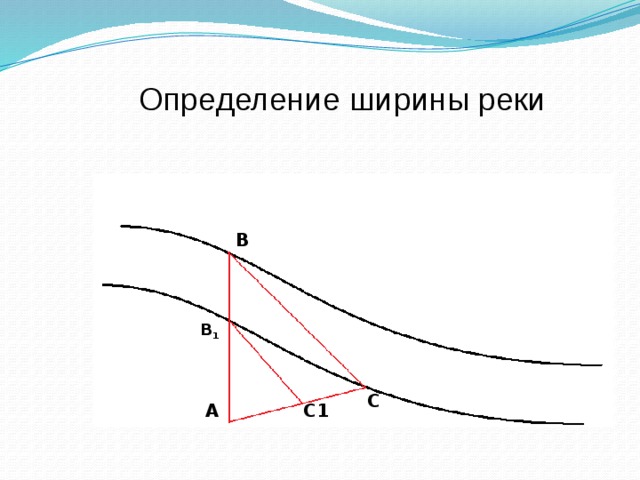
Определение ширины реки

Определение ширины реки

до недоступной точки.

до недоступной точки.

до недоступной точки.

до недоступной точки.

до недоступной точки.

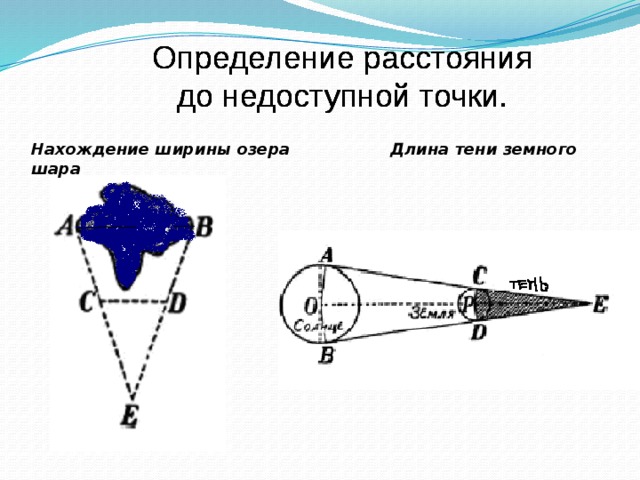
Нахождение ширины озера Длина тени земного шара

В процессе измерения

Измерение с помощью метода Жюль Верна .

Измерение с помощью шеста

Способ при помощью зеркала

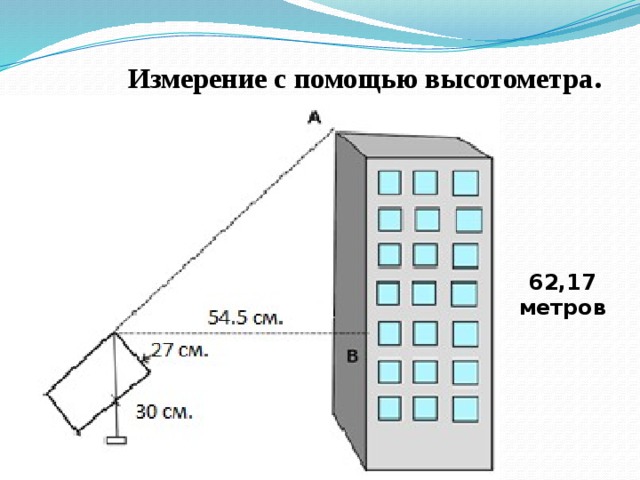
Измерение с помощью высотометра .

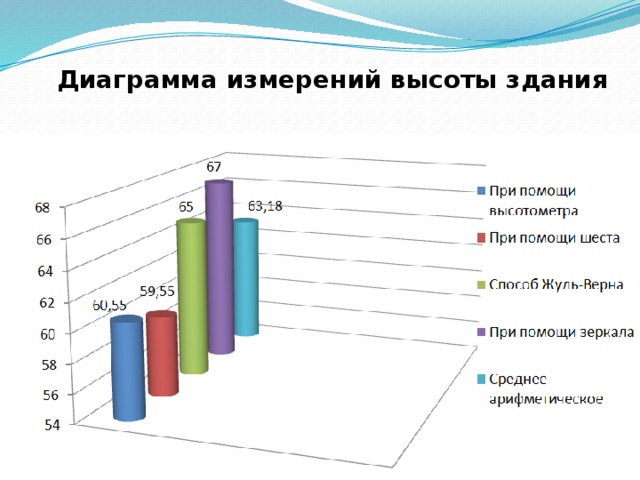
Диаграмма измерений высоты здания

Источник

Проектная работа на тему «Применение подобия треугольников в жизни»

CLK=> 15/3=5=> MD=3*5=15м. Ответ. » data-title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD

CLK=> 15/3=5=> MD=3*5=15м. Ответ. » >

Описание презентации по отдельным слайдам:

Проектная работа на тему: Подобие треугольников и применение их в жизни. Выполнили: ученики 8 класса Чикоткова Арина Ногих Анна Руководитель: учитель математики Фурсенко Н.П. Лизиновка 2016 МКОУ Лизиновская СОШ

Задачи и цели: Узнать где применяется подобие в жизни. Рассмотреть решение задач на местности.

Немного из истории Определение высоты пирамиды по длине ее тени

За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени.

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.

Применение теории на практике: Определение высоты предмета По шесту. Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до основания дерева.

CLK=> 15/3=5=> MD=3*5=15м. Ответ. » title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD

CLK=> 15/3=5=> MD=3*5=15м. Ответ. «> ΔMLD

CLK=> 15/3=5=> MD=3*5=15м. Ответ:» title=»Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD

Решение ∠L-общий,∠DML= =∠KCL=90° => ΔMLD

CLK=> 15/3=5=> MD=3*5=15м. Ответ: дерево высотой 15 м.

10:1.60=6.25 6.25*1.60=10м Ответ : дерево высотой 10 метров 10м

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас

По зеркалу.  АВD подобен EFD (по двум углам):  ВАD= FED=90°;  АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны:

12:1=12 12*1.60=19.2м Ответ: дерево высотой 19.2м 19.2м

Измерение расстояния до недоступной точки. 19.2м 19.2м Палец-0.06м, Расстояние от глаза до пальца-0.5м Расстояние до дерева 160м 19.2:0.06=320 320*0.5=160м

Измерение ширены реки с помощью булавочного прибора

Булавочный прибор для измерений

Также для измерения могут применяться разные инструменты. Экер Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны.

Астролябия Устройство: астролябия состоит из двух частей: диска (лимб), разделённого на градусы, и вращающейся вокруг центра линейки (алидады). При измерении угла на местности она наводится на предметы, лежащие на его сторонах. Наведение алидады называется визированием. Для визирования служат диоптры. Это металлические пластинки с прорезами. Диоптров два: один с прорезом в виде узкой щели, другой с широким прорезом, посередине которого натянут волосок. При визировании к узкому прорезу прикладывается глаз наблюдателя, поэтому диоптр с таким прорезом называется глазным. Диоптр с волоском направляется к предмету, лежащему на стороне измеряемого; он называется предметным. В середине алидады прикреплён к ней компас.

Вывод: Подобие треугольников применяется в повседневной жизни довольно часто. Мы выяснили на конкретных примерах, что с помощью подобия можно найти высоту или расстояние до известной или неизвестной нам точки.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Онлайн-конференция для учителей, репетиторов и родителей

Формирование математических способностей у детей с разными образовательными потребностями с помощью ментальной арифметики и других современных методик

Номер материала: ДБ-296066

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Решение по формату сдачи ЕГЭ в 2022 году будет принято в ближайшее время

Время чтения: 1 минута

Минобрнауки подготовит методику изучения склонности учащихся к агрессии

Время чтения: 2 минуты

В России пройдет конференция «Исследования, улучшающие образование»

Время чтения: 2 минуты

Рособрнадзор оставил за регионами решение о дополнительных школьных каникулах

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

В России объявлены нерабочие дни с 30 октября по 7 ноября

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Класс: 8

Презентации к уроку

Цели и задачи урока:

Ход урока

Слайды 1-2 (Презентация 1)

Геометрия всегда решала те задачи, которые перед ней ставила жизнь. Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие детские игрушки подобны предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, две фотографии разного формата.

Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. Сегодня мы обсудим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности.

Для начала в этом нам помогут герои известного мультфильма «Шрек».

Начнем мы со сказки День Рождения Шрека или Практическое применение подобия треугольников. (Презентация 2)

Слайд 3 (Презентация 1)

Уже в XVI в. В России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Слайд 4 (Презентация 1) Вот один пример.Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнемуконцужезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Дляудобства расчетов и измерений жезл был разделен на 1000 равных частей.

Рассмотрим несколько случаев из истории и литературы.

1. Определение высоты предмета по длине его тени.

Слайд 5-7 (Презентация 1)

Греческие ученые решили множество практических задач, которые до них люди не умели решать. Например, за шесть веков до нашей эры греческий мудрец Фалес Милетский научил египтян определять высоту пирамиды по длине ее тени.

Как это было, рассказывается в книге Я.И. Перельмана «Занимательная геометрия».Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени.

Слайд 8 (Презентация 1)

Я хочу прочитать вам эту маленькую притчу.

«Усталый северный чужеземец пришел в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона и что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.

— Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

— Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

Слайд 9-11 (Презентация 1)

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Он измерил тень от палки и тень от пирамиды. Сравнивая соотношения высот реальных предметов с длинами их теней, Фалес нашел высоту пирамиды.

Определение высоты пирамиды по длине ее тени.

АВС подобен D СDE (по двум углам):

ВСА= СED=90°;

АВС= СDЕ, т. к. соответственные при АВ || DС и секущей АС (солнечные лучи падают параллельно)

В подобных треугольниках сходственные стороны пропорциональны:

.

Таким образом, Фалес нашел высоту пирамиды.

Вопрос классу: Однако, способ предложенный Фалесом, применим не всегда. Почему?

2. Определение высоты предмета по шесту.

Слайд 12-15 (Презентация 1)

При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, которыйживописнопредставлен у Жюль Верна в известном романе «Таинственный остров».

Читаем отрывок из романа.

— Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу.

Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

Взяв прямой шест, длиной 10 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки.

Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком.

— Помнишь свойства подобных треугольников?

— Их сходственные стороны пропорциональны.

— Да, и, следовательно, если мы измерим два расстояния, то зная высоту шеста, сможем вычислить четвёртый неизвестный член пропорции, т.е. высоту стены. Мы обойдёмся, таким образом, без непосредственного измерения этой высоты.

Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

По окончании измерений инженер составил следующую запись:

Н 333,33

Значит, высота гранитной стены равнялась приблизительно 333 футам».

Преимущества способа Жюль Верна:

— можно производить измерения в любую погоду;

3. Определение высоты предмета.

Есть несколько простых способов определения высоты предметов. Например, такие способы приведены в настольной книге охотника-спортсмена.

Слайд 16 (Презентация 1)

По луже. Этот способ можно удачно применять после дождя, когда на земле появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершина предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.

Слайд 17-18 (Презентация 1)

Вместо лужицы можно пользоваться положенным горизонтально зеркальцем. Зеркало кладут горизонтально и отходят от него назад в такую точку, стоя в которой, наблюдатель видит в зеркале верхушку дерева. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека.

АВD подобен D EFD (по двум углам):

ВАD = FED=90°;

АDВ = EDF, т.к. угол падения равен углу отражения.

В подобных треугольниках сходственные стороны пропорциональны:

; .

Таким образом, найдена высота объекта.

4. Определение расстояния до недоступного объекта.

Рассмотрим применение подобия треугольников к определению расстояния до недоступного объекта. Слайд 19-25 (Презентация 1, с использованием Приложения 1).

5. Практическое задание. Слайд 26 (Презентация 1)

Предлагается решить задачу № 583.В ней предлагается, применив подобие треугольников, измерить ширину реки.Чертеж к задаче имеется в учебнике. Ученикам необходимо объяснить, как получен такой чертеж, доказать подобие треугольников и провести вычисления.

По построению АВС подобен АВ₁С₁ (по двум углам).

В подобных треугольниках сходственные стороны пропорциональны:

;;;

6. Рассмотрение и обсуждение примеров. Слайды 27-28 (Презентация 1).

7. Дополнительный материал. Слайд 29-30 (Презентация 1 с использованием Приложения 1)

8. Подведение итогов.

Домашнее задание: пункт 64 параграфа 3, стр. 150-151, № 581, 582, придумать свои задачи на определение высоты предмета и определение расстояния до недоступной точки (оформить либо в виде презентации, либо в виде практической работы в формате А4).

Источник