параллельные плоскости в жизни
Параллельность плоскостей: признак, условие
Всем, кто когда-либо учился или сейчас учится в школе, приходилось сталкиваться с различными трудностями при изучении дисциплин, которые включены в программу, разработанную Министерством образования.
С какими трудностями приходится сталкиваться
Изучение языков сопровождается зазубриванием имеющихся грамматических правил и основных исключений из них. Физкультура требует от учеников большой выкладки, хорошей физической формы и огромного терпения.
Примером могут служить аксиомы, объясняющие теорию параллельности плоскостей, которые необходимо обязательно запомнить, так как они лежат в основе всего курса школьной программы по стереометрии. Давайте попробуем разобраться, как проще и быстрее это можно сделать.
Параллельные плоскости на примерах
Аксиома, указывающая на параллельность плоскостей, звучит следующим образом: «Любые две плоскости считаются параллельными только в том случае, если они не содержат общих точек», то есть не пересекаются друг с другом. Чтобы более детально представить себе данную картину, в качестве элементарного примера можно привести отношение потолка и пола или противоположных стен в здании. Становится сразу понятно, что имеется в виду, а также подтверждается тот факт, что эти плоскости в обычном случае никогда не пересекутся.
Другим примером может служить оконный стеклопакет, где в качестве плоскостей выступают полотна стекол. Они также ни при каких условиях не будут образовывать точек пересечения между собой. Дополнительно к этому можно добавить книжные полки, кубик Рубика, где плоскостями являются его противоположные грани, и прочие элементы быта.
Обозначаются рассматриваемые плоскости специальным знаком в виде двух прямых «||», которые наглядно иллюстрируют параллельность плоскостей. Таким образом, применяя реальные примеры, можно сформировать более четкое восприятие темы, а, следовательно, можно переходить далее к рассмотрению более сложных понятий.
Где и как применяется теория параллельных плоскостей
При изучении школьного курса геометрии ученикам приходится сталкиваться с разносторонними задачами, где зачастую необходимо определить параллельность прямых, прямой и плоскости между собой или зависимость плоскостей друг от друга. Анализируя имеющееся условие, каждую задачу можно соотнести к четырем основным классам стереометрии.
К первому классу относят задачи, в условии которых необходимо определить параллельность прямой и плоскости между собой. Ее решение сводится к доказательству одноименной теоремы. Для этого нужно определить, имеется ли для прямой, не принадлежащей рассматриваемой плоскости, параллельная прямая, лежащая в этой плоскости.
Ко второму классу задач относятся те, в которых задействуют признак параллельности плоскостей. Его применяют для того, чтобы упростить процесс доказательства, тем самым значительно сокращая время на поиск решения.
Следующий класс охватывает спектр задач о соответствии прямых основным свойствам параллельности плоскостей. Решение задач четвертого класса заключается в определении, выполняется ли условие параллельности плоскостей. Зная, как именно происходит доказательство той или иной задачи, ученикам становится проще ориентироваться при применении имеющегося арсенала геометрических аксиом.
Таким образом, задачи, условие которых требует определить и доказать параллельность прямых, прямой и плоскости или двух плоскостей между собой, сводятся к правильному подбору теоремы и решению согласно имеющемуся набору правил.
О параллельности прямой и плоскости
Параллельность прямой и плоскости – особая тема в стереометрии, так как именно она является базовым понятием, на которое опираются все последующие свойства параллельности геометрических фигур.
Согласно имеющимся аксиомам, в случае когда две точки прямой принадлежат некоторой плоскости, можно сделать вывод, что данная прямая также лежит в ней. В сложившейся ситуации становится ясно, что возможны три варианта расположения прямой относительно плоскости в пространстве:
Нас, в частности, интересует последний вариант, когда отсутствуют какие-либо точки пересечения. Только тогда можно говорить о том, что прямая и плоскость относительно друг друга являются параллельными. Таким образом, подтверждается условие основной теоремы о признаке параллельности прямой и плоскости, которая гласит, что: «Если прямая, не принадлежащая рассматриваемой плоскости, параллельна любой прямой на этой плоскости, то рассматриваемая прямая также является параллельной данной плоскости».
Необходимость использования признака параллельности
Признак параллельности плоскостей, как правило, используется для поиска упрощенного решения задач о плоскостях. Суть данного признака состоит в следующем: «Если имеются две пересекающиеся прямые, лежащие в одной плоскости, параллельные двум прямым, принадлежащим другой плоскости, то такие плоскости можно назвать параллельными».
Дополнительные теоремы
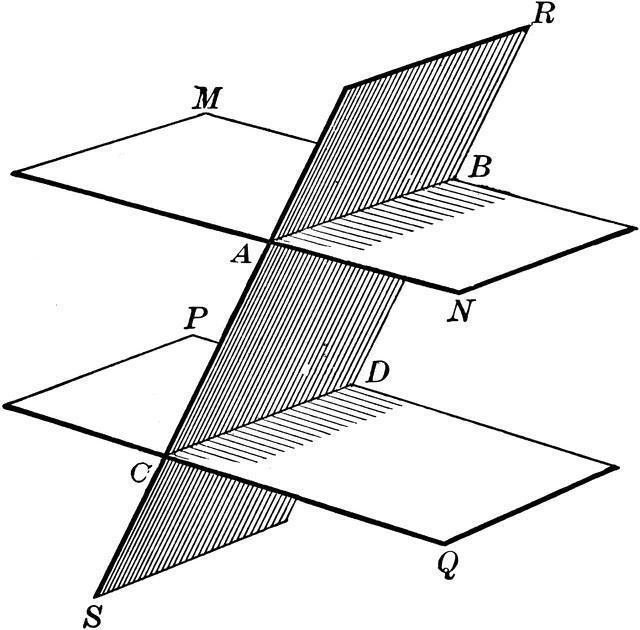
Помимо использования признака, доказывающего параллельность плоскостей, на практике можно встретиться с применением двух других дополнительных теорем. Первая представлена в следующей форме: «Если одна из двух параллельных плоскостей параллельна третьей, то и вторая плоскость либо тоже параллельна третьей, либо полностью совпадает с ней».
Базируясь на использовании приводимых теорем, всегда можно доказать параллельность плоскостей относительно рассматриваемого пространства. Вторая теорема отображает зависимость плоскостей от перпендикулярной прямой и имеет вид: «Если две несовпадающие плоскости перпендикулярны по отношению к некоторой прямой, то они считаются параллельными друг другу».
Понятие необходимого и достаточного условия
При неоднократном решении задач доказательства параллельности плоскостей было выведено необходимое и достаточное условие параллельности плоскостей. Известно, что любая плоскость задается параметрическим уравнением вида: А1х+ В1у+ C1z+D1 =0. Наше условие базируется на использовании системы уравнений, задающих расположение плоскостей в пространстве, и представлено следующей формулировкой: «Для доказательства параллельности двух плоскостей необходимо и достаточно, чтобы система уравнений, описывающих эти плоскости, была несовместной, то есть не имела решения».
Основные свойства
Однако при решении геометрических задач использования признака параллельности не всегда бывает достаточно. Иногда возникает ситуация, когда необходимо доказать параллельность двух и более прямых в различных плоскостях или равенство отрезков, заключенных на этих прямых. Для этого применяют свойства параллельности плоскостей. В геометрии их насчитывается всего два.
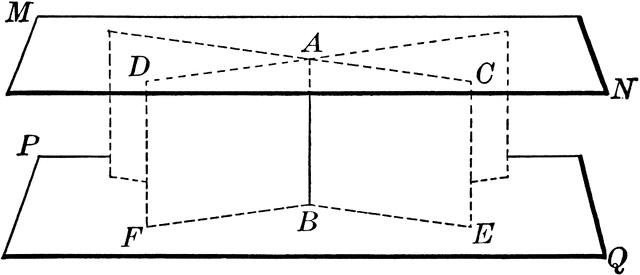
Первое свойство позволяет судить о параллельности прямых в определенных плоскостях и представлено в следующем виде: «Если две параллельные плоскости пересечь третьей, то прямые, образованные линиями пересечения, будут также параллельны друг другу».
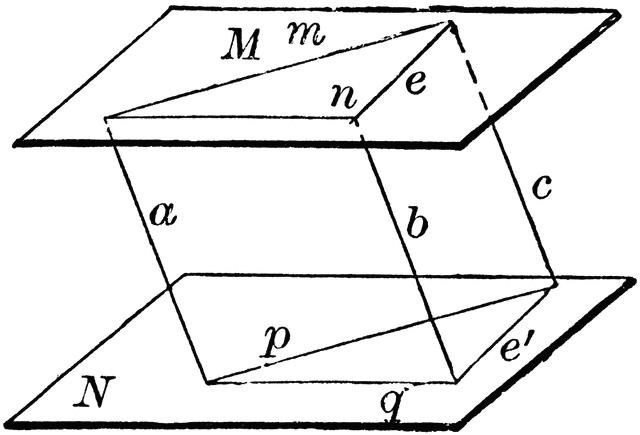
Смысл второго свойства состоит в том, чтобы доказать равенство отрезков, расположенных на параллельных прямых. Его трактовка представлена ниже. «Если рассматривать две параллельные плоскости и заключить между ними область, то можно утверждать, что длина образованных этой областью отрезков будет одинакова».
Класс: 10
Презентация к уроку
Для уроков по стереометрии разработано уже много интересных и полезных презентаций, на пример презентации учителей математики Савченко Е.М. (http://le-savchen.ucoz.ru/load) и Афанасьевой С.В. (asv420@mail.ru), но появилось желание разработать свою презентацию.
Хочется отметить положительные, с моей точки зрения, данной работы:
2. Остановлюсь подробно на кадре № 14. Левая часть этого кадра запись доказательства теоремы из предыдущего кадра, разбитая на этапы. А правая часть – ссылки на ранее изученный материал.
Доказательство теоремы, разложенное на этапы с расставленными акцентами на уже изученную теоретическую базу для выводов каждого этапа, позволяет выявить все причинно-следственные связи этой теоремы.
3. Подведение итога в виде проведения теста с последующей проверкой тоже представляется мне рациональным моментом данной презентации. Можно предположить, что кому-то покажется, что файл № 20 перегружен текстом. Дело в том, что это вопросы устного опроса, но не все учащиеся воспринимают вопрос на слух, поэтому я поддерживают его еще и видеорядом и последовательным медленным анимационным эффектом.
4. В кадрах 15-17 я привожу полное решение задач № 51 и 53. А в задаче 54 привожу лишь правильно выполненный чертеж, а решение учащиеся запишут на доске и в тетрадях.
В Приложении я привожу самоанализ моего урока, с уверенностью, что он может пригодиться молодым коллегам.
I. Организационный момент
Сообщить тему урока и сформулировать цели урока.
П. Актуализация знаний учащихся
III. Изучение нового материала
Кадр 2. Стихотворение Анатолия Кудрявцева «Параллельный мир – нечто, состоящее из слов и линий».
Кадр 3. Определение параллельных плоскостей.
Кадры 4-10. Примеры параллельных плоскостей в жизни, природе, технике, живописи.
Кадр 11. Еще раз определение параллельных плоскостей.
Кадр 12-13. Признак параллельности плоскостей: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Кадр 14. Какие теоремы мы использовали при доказательстве признака?
Обсуждение причинно-следственных связей этой теоремы:
 | Признак параллельности прямой и плоскости: Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости. |
Пусть  | Делаем предположение, противное заключению |
Тогда  | Теорема о линии пересечения плоскостей: Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. |
 | Теорема о параллельности трех прямых в пространстве Если две прямые параллельны третьей прямой, то они параллельны. |
| Находим противоречие условию: через точку М проходят две прямые а и b, параллельные прямой с. | Теорема о параллельных прямых |
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.


IV. Закрепление изученного материала
Кадр 15. № 51. (еще один признак параллельности плоскостей).
Кадр 16-17. № 53.
Кадр 18. № 54.
V. Подведение итогов (в форме текста)
Кадр 21. Рефлексия: Проверяем выполнение задания.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| да | нет | да | нет | да | нет | нет | нет | нет | да |
Кадр 22. Домашнее задание
П. 10, № 55, 56, 57.
Пояснения к домашнему заданию: при выполнении № 55 перепишите в тетрадь приведенное в учебнике решение задачи и разберите его.
Дополнительная задача. Прямая а параллельна плоскости a. Существует ли плоскость, проходящая через прямую а и параллельная плоскости a. Если существует, то сколько таких плоскостей? Ответ обоснуйте.
Параллельные плоскости и их свойства.
С параллельными плоскостями мы встречаемся в жизни каждый день. Наиболее наглядный пример – это плоскости потолка и пола (если не брать в расчёт дизайнерские фантазии); это полки в шкафу; это плоскости ступеней (на которые мы наступаем), ну и т.д., и т.п.
Определение. Две плоскости в трёхмерном пространстве называются параллельными, если они не имеют общих точек.
На чертежах параллельные плоскости изображаются в виде одинаковых параллелограммов, которые смещены друг относительно друга, причём, если они расположены близко друг к другу, то не забывайте о невидимых линиях!
Определение. Две прямые в трёхмерном пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
ТЕОРЕМА (признак параллельности плоскостей). Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то такие плоскости параллельны.
Свойства параллельных плоскостей.
ТЕОРЕМА 1 (о пересечении двух параллельных плоскостей третьей).
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны.
ТЕОРЕМА 2 (о существовании и единственности плоскости, параллельной данной).
Через точку, расположенную вне данной плоскости, можно провести единственную плоскость, параллельную данной.
ТЕОРЕМА 3 (об отрезках параллельных прямых между параллельными плоскостями).
Отрезки параллельных прямых, отсекаемые параллельными плоскостями, равны между собой.
ТЕОРЕМА 4 (о транзитивности отношения параллельности плоскостей).
Если две различные плоскости параллельны третьей плоскости, то они параллельны между собой.