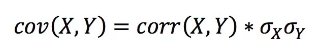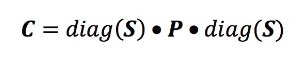np random seed что это
Python: Как использовать метод random.seed()
Функция random() в Python используется для генерации псевдослучайных чисел. Он генерирует числа для некоторых значений, называемых seed значением.
Как работает функция seed?
Функция начального числа используется для хранения случайного метода генерации одних и тех же случайных чисел при многократном выполнении кода на одной или разных машинах.
Начальное значение имеет важное значение для компьютерной безопасности, поскольку оно псевдослучайно создает безопасный секретный ключ шифрования. Таким образом, используя настраиваемое начальное значение, вы можете инициализировать безопасный генератор псевдослучайных чисел в нужном вам месте.
Python random seed
Функция random.seed() в Python используется для инициализации случайных чисел. По умолчанию генератор случайных чисел использует текущее системное время. Если вы дважды используете одно и то же начальное значение, вы получите один и тот же результат, что означает случайное число дважды.
Синтаксис
Параметры
Пример
Этот пример демонстрирует, что если вы дважды используете одно и то же начальное значение, вы дважды получите одно и то же случайное число.
Давайте посмотрим на другой пример, в котором мы генерируем одно и то же случайное число много раз.
Когда мы передаем определенное начальное число в генератор случайных чисел, каждый раз, когда вы выполняете программу, вы получаете одни и те же числа. Это полезно, когда вам нужен предсказуемый источник случайных чисел.
Это упрощает оптимизацию кодов, когда для тестирования используются случайные числа. Вывод кода иногда зависит от ввода. Поэтому использование случайных чисел для тестирования алгоритмов может быть проблематичным.
Кроме того, функция seed используется для генерации одних и тех же случайных чисел снова и снова и упрощает процесс тестирования алгоритма.
Python Random.seed () – глубокое погружение
Введение Случайный – это встроенный модуль в Python, который генерирует псевдослучайные числа. Теперь случайные данные, сгенерированные этим модулем, не совсем случайно. Вместо этого он является псевдо-случайным, как упоминалось ранее. 📚 ПРИМЕЧАНИЕ. «Истинное случайное число» может быть сгенерировано Trng (истинным генератором случайных чисел), когда создается «псевдослучайное число» … Python Random.seed () – Deep Dive Подробнее »
Вступление
Случайные это встроенный модуль в Python, который генерирует псевдослучайная числа. Теперь случайные данные, сгенерированные этим модулем, не совсем случайно. Вместо этого он является псевдо-случайным, как упоминалось ранее.
📚 Примечание: А «Истинное случайный номер» может быть сгенерирован Trng (истинный генератор случайных номеров) во время A «Псевдослучайное число» генерируется PRNG (Pseudorandom Number Generator).
⚠️ Trng находится за пределами объема обсуждения в этой статье.
Итак, Что такое PRNG (генератор номера псевдоранда)? 🧐.
Случайные Модуль имеет набор методов, которые помогают нам генерировать случайные элементы (числа). В этом руководстве мы будем сосредоточиться на Семя () Метод Случайные модуль Отказ
🖋️ Случайное семя () Метод в Python
Генератор случайных номеров нуждается в начальной точке, то есть, она нуждается в Значение семян начать генерацию последовательности случайных чисел. Таким образом, это Семя () Метод, который используется для инициализации генератора случайных чисел.
🚀 По умолчанию Текущее системное время используется генератором случайного номера в качестве начальной точки. Чтобы настроить начальный номер генератора случайного номера, вы должны использовать Семя () метод.
🖋️ Как генерировать одно и то же случайное целое число каждый раз?
Если вы установите одинаковую Семя Значение перед вызовом любой функции случайных модулей, вы получите одно и то же число несколько раз.
Объяснение: В вышеуказанном выходе мы получили тот же номер, что и вывод, потому что одинаковое семя было установлено перед использованием Рэннт каждый раз.
🌱 Сравниваемые () и Random.Choice ()
Вы можете использовать пользовательское значение семян, чтобы получить значение одного и того же выбора снова и снова. Давайте посмотрим на следующий пример.
Python 3: Генерация случайных чисел (модуль random)¶
«Генерация случайных чисел слишком важна, чтобы оставлять её на волю случая»
Python порождает случайные числа на основе формулы, так что они не на самом деле случайные, а, как говорят, псевдослучайные [1]. Этот способ удобен для большинства приложений (кроме онлайновых казино) [2].
| [1] | Википедия: Генератор псевдослучайных чисел |
| [2] | Доусон М. Программируем на Python. — СПб.: Питер, 2014. — 416 с.: ил. — 3-е изд |
Модуль random позволяет генерировать случайные числа. Прежде чем использовать модуль, необходимо подключить его с помощью инструкции:
random.random¶
random.random() — возвращает псевдослучайное число от 0.0 до 1.0
random.seed¶
random.seed( ) — настраивает генератор случайных чисел на новую последовательность. По умолчанию используется системное время. Если значение параметра будет одиноким, то генерируется одинокое число:
random.uniform¶
random.randint¶
random.choince¶
random.choince( ) — возвращает случайный элемент из любой последовательности (строки, списка, кортежа):
random.randrange¶
random.shuffle¶
random.shuffle( ) — перемешивает последовательность (изменяется сама последовательность). Поэтому функция не работает для неизменяемых объектов.
Вероятностные распределения¶
random.expovariate(lambd) — экспоненциальное распределение. lambd равен 1/среднее желаемое. Lambd должен быть отличным от нуля. Возвращаемые значения от 0 до плюс бесконечности, если lambd положительно, и от минус бесконечности до 0, если lambd отрицательный.
random.gauss(значение, стандартное отклонение) — распределение Гаусса.
random.normalvariate(mu, sigma) — нормальное распределение. mu — среднее значение, sigma — стандартное отклонение.
random.vonmisesvariate(mu, kappa) — mu — средний угол, выраженный в радианах от 0 до 2π, и kappa — параметр концентрации, который должен быть больше или равен нулю. Если каппа равна нулю, это распределение сводится к случайному углу в диапазоне от 0 до 2π.
random.paretovariate(alpha) — распределение Парето.
random.weibullvariate(alpha, beta) — распределение Вейбулла.
Примеры¶
Генерация произвольного пароля¶
Хороший пароль должен быть произвольным и состоять минимум из 6 символов, в нём должны быть цифры, строчные и прописные буквы. Приготовить такой пароль можно по следующему рецепту:
Этот же скрипт можно записать всего в две строки:
Данная команда является краткой записью цикла for, вместо неё можно было написать так:
Данный цикл повторяется 12 раз и на каждом круге добавляет к строке psw произвольно выбранный элемент из списка.
Готовимся к собеседованию: случайные числа в Python
Случайность управляет миром, а вы будете управлять случайностью. С помощью Python, конечно.
Чтобы имитировать бросок кубика в игре или предсказать загруженность интернет-ресурса, нужны случайные числа.
Мы разобрали самые популярные вопросы о случайных числах в Python с собеседований. Чаще всего для ответа достаточно написать код и кратко его прокомментировать. Да пребудет с вами Великий Рандом!
Главное, что нужно помнить
С некоторых пор утверждает, что он data scientist. В предыдущих сезонах выдавал себя за математика, звукорежиссёра, радиоведущего, переводчика, писателя. Кандидат наук, но не точных. Бесстрашно пишет о Data Science и программировании на Python.
Вопрос 1. Что такое случайные числа?
Что нужно помнить: случайные числа — это математическое понятие, и их не следует путать с обыденными, произвольными числами. Случайное число в математике и программировании — это:
Другими словами, существует закон или правило, которое называется «функцией распределения» или просто «распределением». И это самое распределение «раздаёт» каждому числу из диапазона определённую вероятность выпадения.
В качестве диапазона значений математикам и программистам привычнее всего использовать диапазон действительных чисел от 0 до 1, но это могут быть и целые числа от 1 до 6, как в игральном кубике, или от 100 до 1 000 000 — и так далее. Главное, что и распределение, и диапазон известны заранее, а само число нет.
Итого: случайные числа — это искусственно полученная последовательность чисел из определённого диапазона, которая подчиняется одному из законов распределения случайной величины.
Распределения бывают разные. Так, равномерное распределение — это когда любое значение из диапазона имеет одну и ту же вероятность выпадения (как у игрального кубика или монетки). Если же распределение, например, нормальное (гауссиана), то чаще выпадают числа из середины диапазона. Есть даже таблица — она поможет выбрать подходящее распределение.
Вопрос 2. Как получить случайные числа в Python?
Основных способов два: с помощью «родной» библиотеки random и с помощью модуля numpy.random из библиотеки numpy.
Прежде чем интервьюер придерётся, не забудьте сказать, что и random, и numpy.random — генераторы псевдослучайных чисел (о них ниже). Истинно случайные числа можно получить, например, c сайта Random.Org: там они генерируются с помощью атмосферного шума.
Библиотека random имеет меньший объём, чем numpy.random, и проще в использовании. Зато numpy.random содержит дополнительные распределения для научных вычислений, а также функции для генерирования целых массивов случайных данных.
В первой строчке мы импортировали default_rng — это «генератор генераторов» случайных массивов из модуля numpy.random. Во второй — создали экземпляр такого генератора и присвоили ему имя rng. В третьей использовали его метод standard_normal, чтобы получить numpy-массив из 10 случайных чисел, и записали массив в переменную vals.
Вопрос 3. Псевдослучайные числа
Псевдослучайные числа — это, если очень упрощать, последовательность чисел, которая только выглядит случайной, а на самом деле каждое число в ней определяется алгоритмом, то есть вычисляется. Псевдослучайные последовательности цикличны: через какой-то период все числа повторяются в точности в том же порядке.
Библиотека random и модуль numpy.random содержат в себе генератор не истинно случайных, а именно псевдослучайных чисел.
Генерировать истинно случайные числа дорого и сложно. Основная трудность состоит в том, чтобы гарантировать отсутствие какого-либо цикла, правила или алгоритма. Чаще всего истинно случайные числа берут из физического мира: шумов атмосферы, детекторов частиц, колебаний электрического тока или из космического излучения.
То, что псевдослучайная последовательность, в отличие от истинно случайной, воспроизводима, очень удобно для практических задач: часто нужно подать на вход ту же самую последовательность второй раз, чтобы посмотреть, как работает программа после добавления новых фич.
Наиболее популярный современный алгоритм генерирования псевдослучайных чисел разработан в 1997 году и носит красивое название «Вихрь Мерсенна». Он используется и в Python. Последовательность чисел, порождённая им, статистически неотличима от истинно случайной и имеет период, равный числу с шестью тысячами знаков. Этого хватает для задач симуляции и моделирования, но с точки зрения криптографии такая последовательность всё равно небезопасна: для успешной атаки достаточно иметь сравнительно небольшую сгенерированную этим генератором последовательность.
Вопрос 4. Как повторить случайную последовательность?
Истинно случайную последовательность повторить невозможно. Но для повторения псевдослучайных чисел в обеих основных библиотеках — random и numpy.random есть функция seed (), которая отвечает за инициализацию («посев») последовательности.
Передавая аргумент 42 в функцию seed(), мы указываем конкретное место в псевдослучайной последовательности, поэтому команда random.random() в третьей и последней строках выдаёт одинаковое число — оно идёт первым после точки, помеченной как seed (42).
В seed() можно передать целые и дробные числа, а также строки и кортежи. Если оставить скобки пустыми, то в качестве аргумента seed() возьмёт текущее системное время.
Аналогичная функция есть в модуле numpy.random:
Вопрос 5. Красные и зелёные шары
Часто на собеседованиях просят написать программу, связанную с вероятностями. Например, код для численной проверки ответа к задачке «Какова вероятность вытащить зелёный шар из мешка, в котором 1 зелёный и 4 красных шара».
(Ответ ⅕ = 0,2).
Иными словами, если 100 раз вынимать шар из мешка, возвращая его обратно, количество выпадения зелёных шаров должно приближаться к 20. Вариант кода для проверки:
Функция random.choice() случайным образом выбирает значение из заданного диапазона — списка из одного « green» и четырёх « red». Код выведет количество зелёных шаров после 100 попыток.
Вопрос 6. Нечестная монетка
Другой вариант: предположим, у нас есть так называемая «нечестная» монетка, где орёл ( H, «heads») и решка ( T, «tails») выпадают не с вероятностью ½, как положено, а по-другому: орёл с вероятностью p(H) = 0,2, а решка, соответственно, p(T) = 0,8.
Тогда код для проверки будет выглядеть примерно так:
Здесь используется другая функция, choices, в которую вместе со списком значений можно в параметре weights передавать вероятности их выпадения.
Код выведет количество выпавших орлов после 10 000 бросков.
К слову: задачи на нечестные монетки, наряду с поиском n-ного числа Фибоначчи и нахождением угла между часовой и минутной стрелками, кочуют из одного собеседования в другое уже не первый десяток лет. Есть вероятность, что одна из них попадётся и вам.
Вопрос 7. Проиллюстрируйте закон больших чисел
Закон больших чисел (ЗБЧ) говорит, что при увеличении количества попыток случайная величина стремится к своему математическому ожиданию — всё усредняется. Подробнее об этом можно прочитать в нашей статье об основах математики для Data Science.
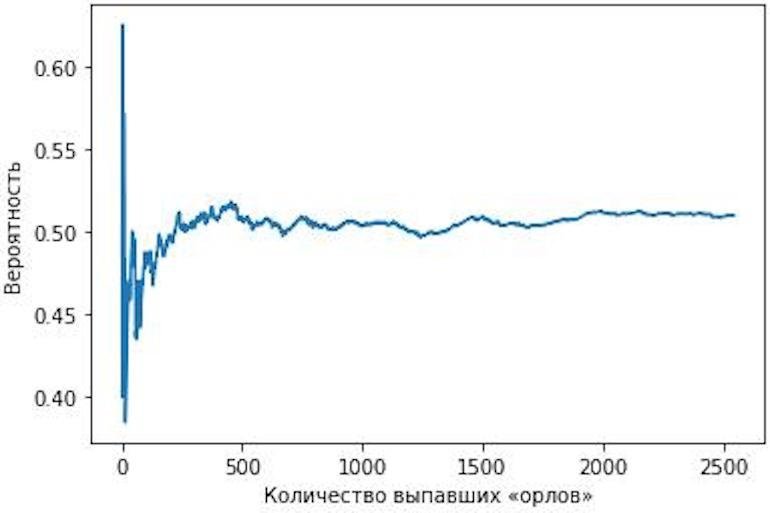
Код для иллюстрации ЗБЧ на примере честной монетки выглядит так:
Вначале мы импортировали уже знакомый нам модуль random и модуль matplotlib.plt — он нужен для рисования простых графиков. После этого определили переменные: общее количество бросков ( total_flips), список из значений вероятностей ( numerical_probability), количество выпавших орлов ( H_count).
Теперь в цикле мы 5 000 раз «подбрасываем» монетку. Если выпадает орёл (« H»), то делим текущее количество выпавших орлов на текущее количество бросков и добавляем итоговое значение в конец списка numerical_probability. В конце рисуем график.
Чем больше бросков, тем ближе к 0,5 вероятность выпадения орла. Всё, как и предсказывает закон больших чисел.
Вопрос 8. Где применяются случайные числа?
В логистике: при расчётах страховых запасов товара — чтобы склад внезапно не опустел или, наоборот, не пришлось держать избыток товара слишком долго. Принято считать, что поведение покупателей случайно и подчиняется одной из разновидностей нормального распределения. В особо запущенных случаях считается случайным даже поведение поставщиков.
В науке: с помощью метода Монте-Карло учёные моделируют поведение частиц во фрактальном окружении в трёхмерном пространстве. Метод Монте-Карло основан на использовании большого количества генерируемых случайных чисел.
В микроэлектронике: броуновское движение частиц играет важную роль в формировании пористости плёночного покрытия полупроводников при напылении его на поверхность. Просчитать это на компьютере гораздо дешевле, чем экспериментировать с реальным покрытием, поэтому сначала его рассчитывают, а потом запускают в производство.
В криптографии: для генерации шифровальных ключей. Здесь становится особенно важным различие между псевдослучайными и истинно случайными числами.
Случайности не случайны
А чтобы никакая псевдослучайность не помешала вам успешно пройти собеседование, приходите в наш Шаолинь на курс «Профессия Python-разработчик». Вы изучите random, numpy и ещё много приёмов пайтонического кунг-фу, а мы поможем с наставниками, единомышленниками и, конечно, с трудоустройством.
Персонаж мультфильма «Кунг-фу Панда», старая мудрая черепаха, учитель и основоположник кунг-фу.
Генерация случайных данных в Python (Руководство)
Насколько случайны случайности? Это странный вопрос, но желательно его задать, если речь идет об информационной безопасности. Когда вы генерируете случайные данные, числа или строки в Python, неплохо иметь хотя бы приблизительное представление о том, как именно генерируются эти данные.
Содержание:
Здесь мы рассмотрим несколько различных способов генерации данных в Python и перейдем к их сравнению в таких категориях, как безопасность, универсальность, предназначение и скорость.
Мы обещаем, что данное руководство не будет похоже на урок математики, или криптографии: математики здесь будет ровно столько, сколько необходимо!
Насколько случайны случайности?
Во первых, нужно сделать небольшое заявление. Большая часть случайных данных, сгенерированных в Python — не совсем “случайная” в научном понимании слова. Скорее, это псевдослучайность, сгенерированная генератором псевдослучайных чисел (PRNG), который по сути, является любым алгоритмом для генерации на первый взгляд случайных, но все еще воспроизводимых данных.
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
“Настоящие” случайные числа могут быть сгенерированы при помощи (как вы, скорее всего, можете догадаться), настоящим генератором случайных чисел (true random number generator, TRNG). Пример: регулярно поднимать игральный кубик с пола, подбрасывать его в воздух и дать ему приземлиться.
Представим, что вы совершаете бросок произвольно и понятия не имеете, какое число выпадет на кубике. Бросок кубика — это грубая форма использования аппаратного обеспечения для генерации числа, которое не является детерминированным. TRNG выходит за рамки этой статьи, однако это стоит упомянуть в любом случае, хотя бы для сравнения.
PRNG, выполняемые обычно программным, а не аппаратным обеспечением, немного отличаются. Вот краткое описание:
Они начинают со случайного числа, также известного как зерно и затем используют алгоритм для генерации псевдослучайной последовательности битов, основанных на нём.
В какой-то момент вам могут посоветовать почитать документацию. И эти люди не то, что ошибутся. Вот интересный сниппет из документации модуля random, который вам не стоит упускать:
Внимание: псевдослучайные генераторы этого модуля не должны быть использованы в целях безопасности (источник).
Возможно, вы уже сталкивались с random.seed(999), random.seed(1234), или им подобным. Этот вызов функции проходит через генератор случайных чисел, который используется модулем random Python. Это то, что делает последующие вызовы генератора случайных чисел детерминированными: вход А производит выход Б. Это чудо может стать проклятием, если используется неправильно.
Возможно термины “случайный” и “детерминированный” выглядят так, будто не могут упоминаться в одном контексте. Чтобы прояснить этот момент, вот супер упрощенная версия random(), которая итеративно создает “случайное” число, используя x = (x * 3) % 19.
“Х” изначально определен как значение сид (cлучайное начальное значение), после чего превращается в детерминированную последовательность чисел, основанных на этом семени:
Не стоит воспринимать этот пример слишком буквально, так как он служит чисто для отображения концепции. Если вы используете значение сид 1234, дальнейшая последовательность вызовов random() всегда должна быть идентичной:
Мы рассмотрим более серьезную иллюстрацию данного примера в дальнейшем.
Что значит “криптографически безопасно”?
Если вам казалось, что в статье мало акронимов типа “RNG” — то добавим сюда еще один: CSPRNG — криптографически безопасный PRNG. CSPRNG подходят для генерации конфиденциальных данных, таких как пароли, аутентификаторы и токены. Благодаря заданной случайно строке, условный злодей не сможет определить, какая строка шла за или перед этой строкой в последовательности случайных строк.
Еще один термин, с которым вы можете столкнуться — энтропия. В двух словах, она ссылается на количество случайностей, желаемых или введенных. Например, один модуль Python, который мы рассмотрим в данной статье, определяет DEFAULT_ENTROPY = 32, количество возвращаемых байтов по умолчанию. Разработчики считают это количество байтов “достаточным”.
Обратите внимание: В данной статье я предполагаю, что байт ссылается на 8 битов, как в далеких 60-х, а не к какой-либо другой единице хранения. Можете называть его октетом, если хотите.
Главная суть CSPRNG — это то, что они все еще псевдослучайные. Они сконструированы таким образом, что являются внутренне детерминированными, но добавляют некие другие переменные, или имеют определенную собственность, которая делает их “достаточно случайными”, чтобы запретить поддержку любой функции, которая выполняет детерменизм.
Что вы из этого почерпнете?
Практически, это значит, что вам нужно использовать PRNG для статистического моделирования, симуляции и сделать случайные данные воспроизводимыми. PRNG также значительно быстрее, чем CSPRNG, что вы и увидите в дальнейшем. Используйте CSPRNG для безопасности и в криптографических приложениях, где конфиденциальные данные являются обязательным условием.
В дополнение к расширению использования вышеупомянутых примеров в этой статье, вы познакомитесь с инструментами Python для работы как с PRNG, так и с CSPRNG:
Мы рассмотрим все вышеперечисленное и подытожим детальным сравнением.
PRNG в Python
Модуль random
Возможно самый известный инструмент для генерации случайных данных в Python — это модуль random, который использует алгоритм PRNG под названием Mersenne Twister в качестве корневого генератора.
Ранее, мы затронули random.seed(), и теперь настало подходящее время, чтобы узнать, как он работает. Сначала, давайте создадим случайные данные без сидинга. Функция random.random() возвращает случайное десятичное число с интервалом [0.0, 1.0). В результате всегда будет меньше, чем правая конечная точка (1.0). Это также известно, как полуоткрытый диапазон:
Если вы запустите этот код лично, весьма вероятно, что полученные числа на вашем компьютере будут другими. По умолчанию, когда вы не используете сид генератор, вы используете текущее системное время, или “источник случайности” вашей операционной системы, если это доступно.
С random.seed() вы можете сделать результаты воспроизводимыми, и цепочка вызова, после random.seed(), будет генерировать один и тот же след данных:
Обратите внимание на повторение “случайных” чисел. Последовательность случайных чисел становится детерменированной, или полностью определенной значением сида, 444.
Давайте рассмотрим основы того, как функционирует модуль random. Ранее мы создали случайное десятичное число. Вы можете сгенерировать случайное целое число между двумя отметками в Python при помощи функции random.randint(). Таким образом охватывается целый интервал [x, y] и обе конечные точки могут быть включены:
С random.randrange(), вы можете исключить правую часть интервала, то есть сгенерированное число всегда остается внутри [x, y) и всегда будет меньше правой части:
Если вы хотите сгенерировать случайные десятичные числа, которые находятся в определенном интервале [x, y], вы можете использовать random.uniform(), который вырывается из непрерывного равномерного распределения:
Чтобы взять случайный элемент из последовательности, не являющейся пустой (такой как список или кортеж), вы можете использовать random.choice(). Также есть random.choices() для выборки нескольких элементов из последовательности с заменой (дубликаты возможны):
Вы можете сделать последовательность случайной прямо на месте, при помощи random.shuffle(). Таким образом удастся обновить объект последовательности и сделать порядок элементов случайным:
Если вы не хотите делать это с изначальным списком, сначала вам может понадобиться сделать копию, а потом уже перемешать её. Вы можете создавать копии списков Python при помощи модуля copy, или просто x[:], или x.copy(), где x является списком.
Перед тем, как перейти к генерированию случайных данных в NumPy, давайте рассмотрим еще одно приложение, которое частично включено в процесс: генерация последовательности уникальных случайных строк с одинаковой длиной.
В первую очередь, это может разобраться с устройством функции. Вам нужно выбрать из “пула” символов, таких как буквы, числа, и\или знаки препинания, совмести их в одну строку, и затем проверить, является ли эта строка сгенерированной. Python работает отлично для такого типа тестирования:
«».join() присоединяет буквы из random.choices() в простую строку, где «k» это длинна строки. Это токен добавлен в набор, который не может иметь дубликатов, и цикл while будет проходить, пока набор не будет содержать количество элементов, которое вы определили.
На заметку: Модуль string содержит ряд полезных констант: cii_lowercase, ascii_uppercase, string.punctuation, ascii_whitespace и еще много других.
Давайте проверим эту функцию:
Для хорошо настроенной версии этой функции, этот ответ Stack Overflow использует функции генератора, привязку имени и еще несколько продвинутых хитростей, чтобы создать более быструю, криптографически безопасную версию упомянутой ранее unique_strings().
PRNG для массивов: numpy.random
Одна вещь, которую вы могли заметить, заключается в том, что большинство функций из случайного числа возвращают скалярное значение (один int, float, или другой объект). Если вы хотели сгенерировать последовательность случайных чисел, один из способов достичь этого — охватить список Python:
Есть еще один вариант, который был разработан как раз для этого. Вы можете рассматривать пакет numpy.random от NumPy как стандартный модуль random библиотеки Python, но только для массивов NumPy. (Он также имеет возможность рисовать из гораздо большего количество статистических распределений).
Обратите внимание на то, что numpy.random использует собственные PRNG, которые отделены от обычных случайных чисел. Вы не будете создавать детерминестически случайные массивы NumPy с вызовом random.seed():
Без дальнейших церемоний, вот несколько примеров, удовлетворяющих ваш аппетит:
В синтаксе для randn(d0, d1, …, dn), параметры d0, d1, …, dn являются опциональными и указывают форму итогового объекта. Здесь, np.random.randn(3, 4) создает 2d массив с 3 строками и 4 столбцами. В качестве данных будут i.i.d., что означает, что каждая точка данных создается независимо от других.
Еще одна простая операция — это создание последовательности случайных логических значений: True или False. Один из способов сделать это — использовать np.random.choice([True, False]). Однако, будет практически в 4 раза быстрее выбрать (0, 1), а затем отобразить эти целые числа в соответствующие булевские значения:
КОД # randint является [inclusive, exclusive), в отличие от random.randint()
КОД
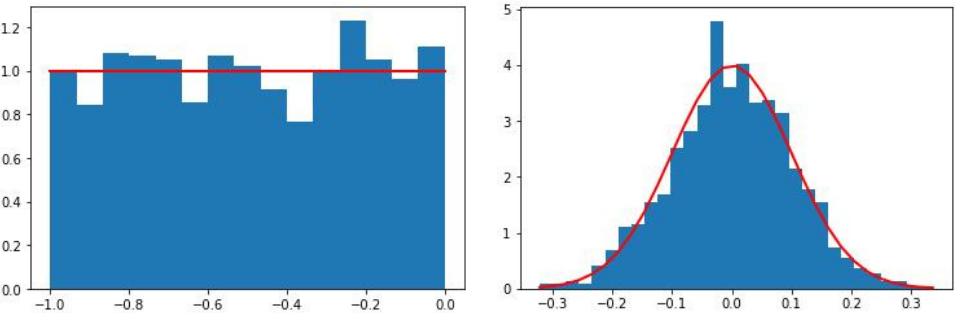
Что на счет генерации коррелированных данных? Скажем, вы хотите симулировать два корелированных временных ряда. Один из способов сделать — это использовать функцию multivariate_normal() нашего NumPy, которая учитывает матрицу ковариации. Другими словами, чтобы списать из одной нормальной распределенной случайной переменной, вам нужно определить ее среднее значение и дисперсию (или стандартное отклонение).
Для выборки из многомерного нормального распределения, вы определяете матрицу ковариации и средние значения, в итоге вы получите несколько взаимосвязанных рядов данных, которые разделены приблизительно нормально.
Однако, в отличие от ковариации, корреляция — это более знакомая для большинства мера, к тому же более интуитивная. Это ковариация, нормализованная продуктом стандартных отклонений, так что вы можете определить ковариацию с точки зрения корреляции и стандартного отклонения:
Итак, можете ли вы списать случайные выборки из многомерного нормального распределения, определив матрицу корреляции и стандартные отклонения? Да, но вам нужно будет получить приведенную выше формулу матрицы. Здесь, S — это вектор стандартных отклонений, P — это их корреляционная матрица, и С — это результирующая (квадратная) ковариационная матрица:
Это может быть выражено в NumPy следующим образом:
Теперь, вы можете сгенерировать два временных ряда, которые коррелируют, но все еще являются случайными:
Вы можете рассматривать данные как 500 пар обратно-коррелированных точек данных. Вот проверка правильности, так что вы можете вернуться к изначальному вводу, который приблизительно соответствует corr, stdev, и mean из примера выше:
Перед тем как мы перейдем к CSPRNG, может быть полезно обобщить некоторые случайные функции и копии numpy.random:
| Модуль random | Аналог NumPy | Использование |
| random() | rand() | Случайное десятичное [0.0, 1.0) |
| randint(a, b) | random_integers() | Случайное целое число [a, b] |
| randrange(a, b[, step]) | randint() | Случайное целое число [a, b) |
| uniform(a, b) | uniform() | Случайное десятичное [a, b] |
| choice(seq) | choice() | Случайный элемент из seq |
| choices(seq, k=1) | choice() | Случайные k элементы из seq с заменой |
| sample(population, k) | choice() с параметром replace=False | Случайные k элементы из seq без замены |
| shuffle(x[, random]) | shuffle() | Перемешка порядка |
| normalvariate(mu, sigma) или gauss(mu, sigma) | normal() | Пример из нормального распределения со средним значением mu и стандартным отклонением sigma |
Обратите внимание: NumPy специализируется на построении и обработке больших, многомерных массивов. Если вам нужно только одно значение, то random будет достаточно, к тому же, еще и быстрее. Для небольших последовательностей, random может быть еще быстрее, так как NumPy имеет ряд дополнительных расходов.
Мы рассмотрели две фундаментальные опции PRNG, так что теперь мы можем перейти к еще более безопасным адаптациям.
CSPRNG в Python
os.urandom(): настолько случайно, на сколько возможно
Функция Python под названием os.urandom() используется как в secrets, так и в uuid (мы к ним скоро придем). Чтобы не вдаваться в лишние подробности, os.urandom() генерирует зависимые от операционной системы случайные байты, которые спокойно можно назвать криптографически надежными: