nn embedding что делает
Делаем прогноз слов рекуррентной сетью Embedding слой
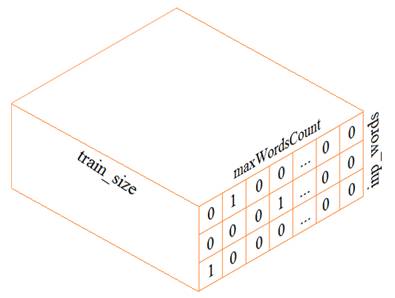
На предыдущем занятии мы с вами построили экспериментальную рекуррентную НС для прогнозирования следующего символа. На этом занятии разовьем эту тему и построим сеть для оценки следующего слова. В целом, сеть будет реализована также как и ранее, а вот подготовка обучающей выборки будет выполняться несколько иначе. В самом простом варианте, нам следует сформировать трехмерный тензор (похожий на тензор из предыдущего занятия):
Из текста будем выделять слова целиком (а не отдельные символы, как ранее). Набор уникальных слов будут составлять наш словарь. Размер этого словаря обозначим через переменную
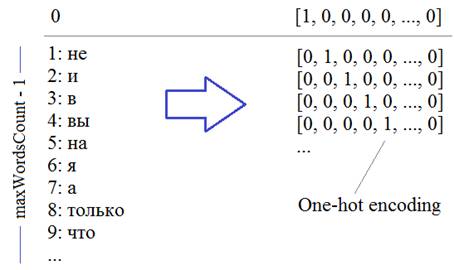
Каждое слово, затем, будет кодироваться one-hot вектором в соответствии с его номером в словаре:
Второй важный параметр – число слов, на основе которых строится прогноз, который определяется переменной:
Давайте теперь посмотрим, как можно сформировать такой тензор. Вначале загрузим тексты с отрицательными высказываниями из файла text:
Теперь нам нужно разбить эти высказывания на слова. Для этого воспользуемся уже знакомым из прошлого занятия инструментом Tokenizer и положим, что максимальное число слов будет равно 1000:
По идее, мы здесь могли бы и не задавать максимальное число слов, тогда эта величина была бы определена автоматически при парсинге текста. Но данный параметр имеет один существенный плюс: из всех найденных слов мы оставляем 999 наиболее часто встречаемых (то есть maxWordsCount-1), то есть, мы имеем возможность отбросить редкие слова, которые особо не нужны при обучении НС.
Конечно, в данном случае, останутся все найденные слова, т.к. их общее число меньше 1000. Вообще, этот параметр устанавливается с позиции «здравого смысла». Например, при большой обучающей выборке, скорее всего, мы будем иметь дело с большинством слов (и их форм) русского языка. Какой лексический запас слов у среднестатистического человека? Около 10 000. Значит, для большой выборки можно указать значение
и это будет хорошим выбором.
Итак, мы разбили текст на слова и для примера выведем их начальный список:
Здесь отображаются кортежи со словом и его частотой встречаемости в тексте.
Далее, мы преобразуем текст в последовательность чисел в соответствии с полученным словарем. Для этого используется специальный метод класса Tokenizer:
На выходе получим массив чисел объекта numpy:
Осталось закодировать числа массива data в one-hot векторы. Для этого мы воспользуемся методом to_categorical пакета Keras:
На выходе получим двумерную матрицу, состоящую из One-hot векторов:
Затем, из этой матрицы сформируем тензор обучающей выборки и соответствующий набор выходных значений. Для начала вычислим размер обучающего множества:
И, далее, сформируем входной тензор и прогнозные значения также, как мы это делали с символами:
Все, у нас есть обучающая выборка и требуемые выходные значения. Осталось создать модель рекуррентной сети. Мы ее возьмем из предыдущего занятия с числом нейронов скрытого слоя 128 и maxWordsCount нейронами на выходе с функцией активации softmax:
Готово. Запускаем процесс обучения:
И давайте теперь посмотрим, что у нас получилось. Запишем функцию для формирования текста из спрогнозированных слов:
И вызовем ее с тремя первыми словами:
Получим вот такой результат:
позитив добавляет годы счастье вашей жизни и двигаться их в вы держись в и мечты успеха свою жизни не меня за не в
Конечно, немного сумбурно, но в целом, что-то в этом есть. Такой результат еще связан с очень маленькой обучающей выборкой. По идее, здесь нужно взять какую-нибудь большую книгу и прогнать ее через сеть. Но цель этого занятия показать общий принцип использования рекуррентных сетей для прогнозирования слов в последовательности.
Embedding-слой
Однако в такой реализации есть один существенный недостаток: входной тензор, что мы получили, занимает в памяти очень много места. Представьте, если решается реальная задача с числом слов 20 000. Тогда тензора будет содержать:

и требовать значительный объем памяти. Поэтому специалисты по нейронным сетям предложили альтернативный подход – использование специального входного слоя, который получил название:
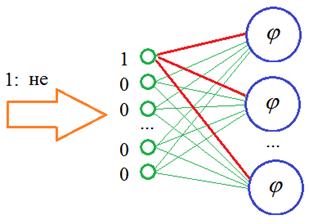
В чем его суть? Смотрите, когда мы подаем вектор с единицей на определенной позиции, то у нас, фактически, используются только связи для этого одного входа, остальные умножаются на 0 и формируют нулевые суммы на всех остальных нейронах скрытого слоя:
И отсюда хорошо видно, что если передавать на вход не такие расширенные векторы, а последовательность с порядковыми номерами слов в словаре:
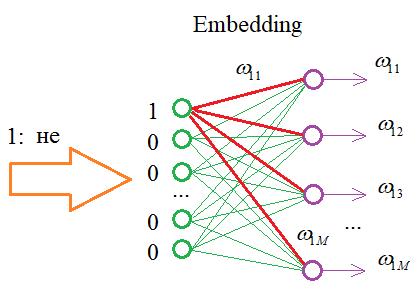
То на входе НС можно реализовать простой алгоритм, который бы подавал 1 на нейрон с соответствующим номером этого слова, а остальные суммы приравнивались бы нулю. В итоге, мы существенно экономим память при хранении обучающей выборки, а результат получаем тот же самый. Именно такую операцию и выполняет Embedding слой. На выходах его слоя формируются выходные значения, равные весам связей для переданной 1:
Далее, эти значения весов подаются уже на следующий слой нейронной сети.
В Keras такой слой можно создать с помощью одноименного класса:
Есть и другие параметры, подробно о них можно почитать на странице документации по ссылке:
Этот слой можно создавать только как входной и в нашем случае мы его определим так:
Здесь 256 – это число выходов в Embedding-слое. В качестве входной обучающей выборки мы теперь можем использовать одномерный массив:
А выходные значения остаются прежними – двумерным массивом из One-hot векторов, так как у нас на выходе 1000 нейронов.
Далее, абсолютно также проводим обучение и немного модифицируем функцию buildPhrase:
И запускаем процесс прогнозирования слов. Как видите, использование Embedding слоя значительно упрощает и саму программу и размер используемой памяти.
Видео по теме
Нейронные сети: краткая история триумфа
Структура и принцип работы полносвязных нейронных сетей | #1 нейросети на Python
Ускорение обучения, начальные веса, стандартизация, подготовка выборки | #4 нейросети на Python
Функции активации, критерии качества работы НС | #6 нейросети на Python
Как нейронная сеть распознает цифры | #9 нейросети на Python
Оптимизаторы в Keras, формирование выборки валидации | #10 нейросети на Python
Batch Normalization (батч-нормализация) что это такое? | #12 нейросети на Python
Как работают сверточные нейронные сети | #13 нейросети на Python
Делаем сверточную нейронную сеть в Keras | #14 нейросети на Python
Примеры архитектур сверточных сетей VGG-16 и VGG-19 | #15 нейросети на Python
Теория стилизации изображений (Neural Style Transfer) | #16 нейросети на Python
Делаем перенос стилей изображений с помощью Keras и Tensorflow | #17 нейросети на Python
Как нейронная сеть раскрашивает изображения | #18 нейросети на Python
Введение в рекуррентные нейронные сети | #19 нейросети на Python
Как рекуррентная нейронная сеть прогнозирует символы | #20 нейросети на Python
Делаем прогноз слов рекуррентной сетью Embedding слой | #21 нейросети на Python
Как работают RNN. Глубокие рекуррентные нейросети | #22 нейросети на Python
Как делать сентимент-анализ рекуррентной LSTM сетью | #24 нейросети на Python
Рекуррентные блоки GRU. Пример их реализации в задаче сентимент-анализа | #25 нейросети на Python
Двунаправленные (bidirectional) рекуррентные нейронные сети | #26 нейросети на Python
Автоэнкодеры. Что это и как работают | #27 нейросети на Python
Вариационные автоэнкодеры (VAE). Что это такое? | #28 нейросети на Python
Делаем вариационный автоэнкодер (VAE) в Keras | #29 нейросети на Python
Расширенный вариационный автоэнкодер (CVAE) | #30 нейросети на Python
Что такое генеративно-состязательные сети (GAN) | #31 нейросети на Python
Делаем генеративно-состязательную сеть в Keras и Tensorflow | #32 нейросети на Python
© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
Как модуль nn.Embedding интуитивно связан с идеей вложения в целом?
Насколько я понимаю, это отображение достигается в процессе обучения, как в автокодировщике. Кодер изучает оптимальное встраивание, чтобы декодер мог восстановить исходный ввод.
Итак, у меня вопрос, как это связано с модулем nn.Embedding :
«учится» ли этот слой более низкоразмерному представлению большего входного пространства? Или это что-то совсем другое?
Я ищу преобразование очень абстрактного языка документации в нечто реальное:
Как вы можете объяснить использование nn.Embedding() в этом случае?
Что означает каждый аргумент в контексте реального мира?
1 ответ
Вот небольшой эксперимент:
Как и ожидалось, loss_before и loss_after отличаются, что показывает, что параметры nn.Embedding можно изучить.
Изменить: ваш вопрос сводится к тому, «как мне закодировать свои данные?».
Для тех примеров, которые вы привели точно:
Скажем, у меня есть ввод x. Этот ввод может быть векторизованным изображением или, возможно, некоторыми последовательными ежедневными данными температуры. В любом случае, этот вход x содержит 100 элементов (100 дней температуры или изображение 10×10).
nn.Embedding обычно используется во главе сети для преобразования закодированных данных в пространство более низкой размерности. Это не решит вашу проблему волшебным уменьшением ваших размеров.
Если у вас есть последовательность температур, которую вы хотите проанализировать. Вы можете закодировать каждую температуру в горячем коде. Но это векторное представление может быть очень большим (в зависимости от количества различных температур). Использование слоя внедрения позволило бы уменьшить размер этих векторов. Это важно, когда целью является анализ данных с помощью RNN или любого другого MLP, если на то пошло. Поскольку чем больше размер вашего ввода, тем больше у вас будет параметров!
Интерфейсы для слоёв
Слои в PyTorch реализованы в двух формах: как функции и как классы.
Слои как экземпляры классов, сами создают параметры с начальными случайными значениями.
Ниже обязательными аргументами при создании класса является число входов nX и число выходов nY слоя (число нейронов в нём == число новых признаков). Затем экземпляру fc класса Linear через оператор ( ) передаётся входная матрица X:
Класс слоя у своих параметров объявляет свойство requires_grad=True. Это приводит к построению вычислительного графа при прямом распространении по сети и к получению градиентов от параметров при обратном распространении:
Дальше идёт небольшой справочник наиболее важных типов слоёв, активационных функций и оптимизаторов. За более подробной информацией стоит обратиться к документации.
Базовые слои
Полносвязный слой
Реализация линейного слоя в torch.nn.functional выглядит следующим образом:
Эмбеддинг
Слой Embedding преобразует массив целых чисел long на входе в матрицу (массив векторов). Подробнее см. Embedding слов. При создании экземпляра слоя обязательны два первых параметра: размер словаря и размерность эмбеддига. Ниже создаётся слой с 5 словами и их 2-мерными (случайными) векторами:
Параметр max_norm задаёт максимальную длину векторов и если при обучении она превышается, вектор перенормируется. В качестве нормы по умолчанию используется сумма квадратов компонент: norm_type = 2.
При параметре scale_grad_by_freq = True градиенты при обучении будут взвешиваться по обратной частоте слов в батче (усиливать изменение более редких слов). Но батч при этом стоит брать достаточно большой. Загрузить готовые векторы можно, создав слой следующим образом:
Параметры функции from_pretrained:
Конволюция
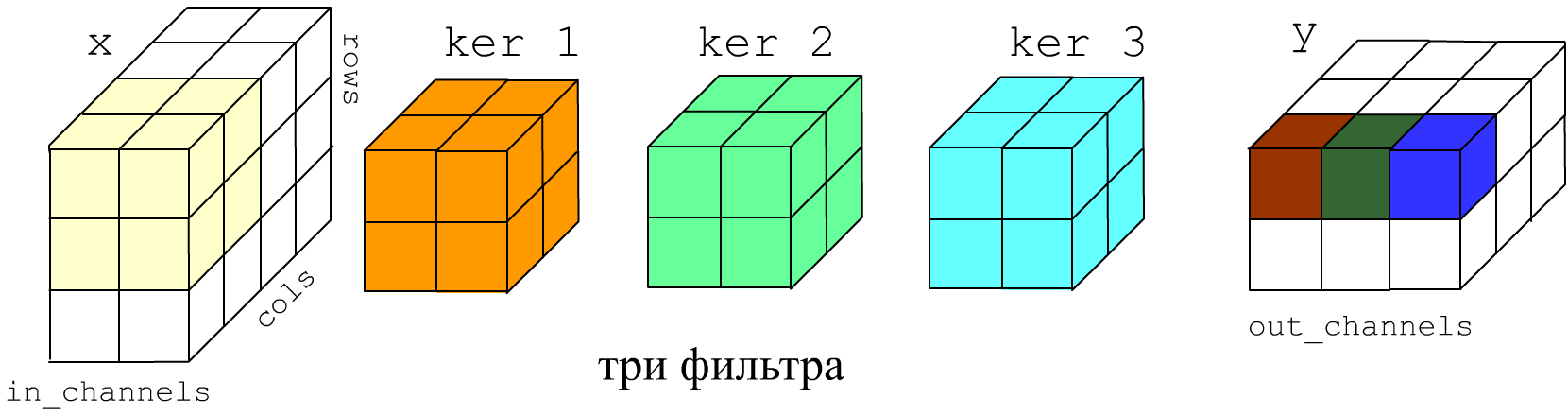
Свёрточный слой Conv2D применяется к «картинкам» высотой rows, шириной cols и имеющих in_channels «цветовых» каналов. На самом деле графические термины условны и слой Conv2D может применяться не только при обработке изображений. Форма входного тензора (N, in_channels, rows, cols). На выходе будет тензор (N, out_channels, rows_out, cols_out) По исходному тензору проходит out_channels фильтров размером kernel_size (число или tuple). Глубина фильтра определяется числом входных каналов in_channels.
Ниже на рисунке in_channels=2, out_channels=3 (три фильтра), размеры фильтров kernel_size = 2 или, что тоже kernel_size = (2,2). Фильтры по умолчанию скользят по картинке с шагом один stride=(1,1), поэтому результирующие ширина и высота картинки на 1 меньше:
Параметр padding (int or tuple) задаёт на сколько «пикселей» необходимо расширить картинку с обоих сторон, перед прохождением по ней фильтрами. Расширенная область заполняется значениями в соответствии с параметром padding_mode: ‘zeros’, ‘reflect’, ‘replicate’, ‘circular’. Параметр dilation = 1 задаёт расстояние между пикселями, попадающими в фильтр.
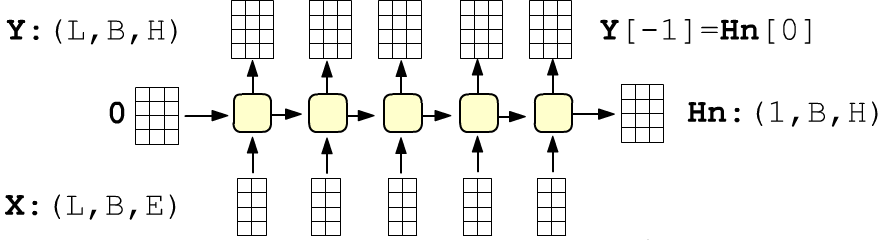
Слой возвращает кортеж из тензора всех выходов сети формы (seq_len, batch_size, hidden_size) и последнего скрытого состояния (последний выход) формы (num_layers, batch_size, hidden_size), где для одного слоя num_layers = 1. По умолчанию компоненты начального скрытого состояние нулевые. Иначе их можно передать вторым аргументом:
В слое можно сразу задать стопку RNN-слоёв ( num_layers) Между слоями можно вставить режим случайного забивания нулями выходов с вероятностью dropout. Слой можно также превратить в двунаправленный: bidirectional = True. В этом случае размерность выхода будет (inputs, batch_size, 2*hidden_size), а размерность начального скрытого состояния (2 * num_layers, batch_size, hidden_size).
MultiheadAttention
Outputs: output: (L,N,E), weights: (N,L,S)
Если эмбединг входов одинаковый, то проекционные матрицы упакованы в in_proj_weight формы (3*E,E), иначе это параметры: q_proj_weight, k_proj_weight, v_proj_weight. Смещение (если он есть) это in_proj_bias формы (3*E,), а выходной слой: out_proj.
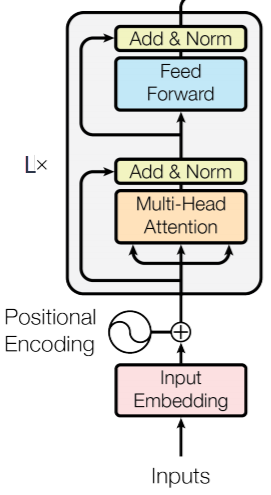
TransformerEncoderLayer
Параметры: d_model – размерность входа (вектора одного токена), nhead – число голов (делитель параметра d_model), dim_feedforward – размерность полносвязной сети.
TransformerEncoder
Cлои без параметров
Лиаринизация тензора
При создании с параметрами по умолчанию, все индексы кроме первого (индекс примера) сольются в один (для каждого примера получится вектор). Слой параметров не имеет.
Косинус между векторами
Расстояние между векторами
Отключение нейронов
В режиме тренировке: m.train(), с вероятностью » p» зануляет каждый элемент матрицы и делит их на 1-p.
В режиме оценивания: m.eval() ничего не делает. Благодаря делению на 1-p среднее значение по модулю элементов в режиме тренировки будет такой-же, как и врежиме оценивания (у входного тензора).
Нормализация тензора
MaxPool2d
AvgPool2d
Активационные функции
Функции ошибки
Среднеквадратичная ошибка
По умолчанию ( reduction=’mean’) квадраты отклонений усредняются по всем примерам батча и по всем выходам (ошибка это скаляр!).
Бинарная кросс-энтропия
Кросс-энтропия
Входные данные в функцию ошибки CE_loss(y, y_t)могут иметь форму y=(B,C):float, y_t=(B,):long или в n-мерном случае: y=(B,C,L1. Ln):float, y_t=(B,L1. Ln):long
Воспроизведём, полученное значение:
Логарифмический максимум правдоподобности
Результат будет таким же как и при CrossEntropyLoss, если последним слоем стоит LogSoftmax.
Word Embeddings: Encoding Lexical Semantics¶
Word embeddings are dense vectors of real numbers, one per word in your vocabulary. In NLP, it is almost always the case that your features are words! But how should you represent a word in a computer? You could store its ascii character representation, but that only tells you what the word is, it doesn’t say much about what it means (you might be able to derive its part of speech from its affixes, or properties from its capitalization, but not much). Even more, in what sense could you combine these representations? We often want dense outputs from our neural networks, where the inputs are \(|V|\) dimensional, where \(V\) is our vocabulary, but often the outputs are only a few dimensional (if we are only predicting a handful of labels, for instance). How do we get from a massive dimensional space to a smaller dimensional space?
How about instead of ascii representations, we use a one-hot encoding? That is, we represent the word \(w\) by
There is an enormous drawback to this representation, besides just how huge it is. It basically treats all words as independent entities with no relation to each other. What we really want is some notion of similarity between words. Why? Let’s see an example.
Suppose we are building a language model. Suppose we have seen the sentences
in our training data. Now suppose we get a new sentence never before seen in our training data:
Our language model might do OK on this sentence, but wouldn’t it be much better if we could use the following two facts:
and then infer that physicist is actually a good fit in the new unseen sentence? This is what we mean by a notion of similarity: we mean semantic similarity, not simply having similar orthographic representations. It is a technique to combat the sparsity of linguistic data, by connecting the dots between what we have seen and what we haven’t. This example of course relies on a fundamental linguistic assumption: that words appearing in similar contexts are related to each other semantically. This is called the distributional hypothesis.
Getting Dense Word Embeddings¶
How can we solve this problem? That is, how could we actually encode semantic similarity in words? Maybe we think up some semantic attributes. For example, we see that both mathematicians and physicists can run, so maybe we give these words a high score for the “is able to run” semantic attribute. Think of some other attributes, and imagine what you might score some common words on those attributes.
If each attribute is a dimension, then we might give each word a vector, like this:
Then we can get a measure of similarity between these words by doing:
Although it is more common to normalize by the lengths:
You can think of the sparse one-hot vectors from the beginning of this section as a special case of these new vectors we have defined, where each word basically has similarity 0, and we gave each word some unique semantic attribute. These new vectors are dense, which is to say their entries are (typically) non-zero.
But these new vectors are a big pain: you could think of thousands of different semantic attributes that might be relevant to determining similarity, and how on earth would you set the values of the different attributes? Central to the idea of deep learning is that the neural network learns representations of the features, rather than requiring the programmer to design them herself. So why not just let the word embeddings be parameters in our model, and then be updated during training? This is exactly what we will do. We will have some latent semantic attributes that the network can, in principle, learn. Note that the word embeddings will probably not be interpretable. That is, although with our hand-crafted vectors above we can see that mathematicians and physicists are similar in that they both like coffee, if we allow a neural network to learn the embeddings and see that both mathematicians and physicists have a large value in the second dimension, it is not clear what that means. They are similar in some latent semantic dimension, but this probably has no interpretation to us.
In summary, word embeddings are a representation of the *semantics* of a word, efficiently encoding semantic information that might be relevant to the task at hand. You can embed other things too: part of speech tags, parse trees, anything! The idea of feature embeddings is central to the field.
Word Embeddings in Pytorch¶
Before we get to a worked example and an exercise, a few quick notes about how to use embeddings in Pytorch and in deep learning programming in general. Similar to how we defined a unique index for each word when making one-hot vectors, we also need to define an index for each word when using embeddings. These will be keys into a lookup table. That is, embeddings are stored as a \(|V| \times D\) matrix, where \(D\) is the dimensionality of the embeddings, such that the word assigned index \(i\) has its embedding stored in the \(i\) ’th row of the matrix. In all of my code, the mapping from words to indices is a dictionary named word_to_ix.