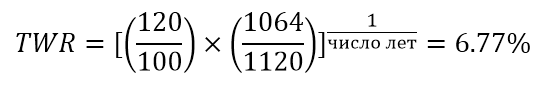mwr доходность что это
Реальная доходность портфеля: расчет и смысл
Некоторое время назад я писал статью о расчете рыночной доходности. Статья несомненно важная и рекомендуется всем, кто имеет дело с инвестициями, поскольку очень многие считают доходность либо неправильно (обычно новички, в частности путая среднеарифметические и среднегеометрические данные), либо намеренно завышают результат (обычно инвестиционные фонды, экстраполируя удачные квартальные показатели в будущее).
Тем не менее у приведенных расчетов есть недостаток. Дело в том, что разовое инвестирование одной суммы (без промежуточных вводов и выводов до выхода из рынка) это скорее гипотетический подход. Даже если не брать во внимание купонные выплаты и дивиденды, которые не всегда могут быть сразу же реинвестированы, реальное инвестирование предполагает периодические вводы и выводы средств, что плохо вписывается в представленные по ссылке формулы.
Два вида доходности: TWR и MWR
В этом случае есть два способа:
Разберемся с ними отдельно.
1. TWR
Считается более традиционной, хотя это можно оспорить. Для ее расчета инвестиционный процесс разбивается на интервалы, в которых происходят ввод или вывод средств, таким образом нивелируя их влияние на результат. В нашем случае инвестиции разбиты на два равных годовых отрезка (число лет =2):
2. MWR
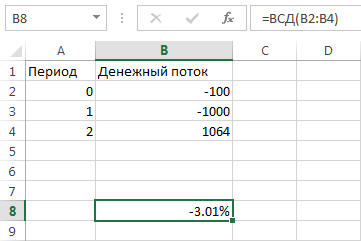
Учесть этот недостаток TWR может доходность, взвешенная по деньгам. Она отражает движение денежных средств и может быть посчитана при помощи функции ВСД в Excel. Для этого нам нужны вносимые средства со знаком «минус» и конечный результат на счете. Для случая выше расчет следующий:
Итого, MWR = – √1 + (3.01%/100%) = –1.49%. Корень означает степень ½, где 2 — число лет инвестиций. Как видно, доходность по деньгам более адекватно описывает поведение нашего реального счета, хотя для ее вычисления мы прописываем только ввод средств и конечный результат. MWR и TWR встречаются в аналитике зарубежных брокеров и в сервисах расчета инвестиционных портфелей.
Итоги
Наша ситуация вполне могла быть обратной: вначале мы получаем заметный минус на малую сумму, затем вносим гораздо больше и фиксируем небольшой плюс. Нетрудно рассчитать, что тогда TWR будет отрицательной, а MWR положительной. Можно сказать, что TWR описывает стратегию инвестора в целом, тогда как MWR включает в нее движения средств — таким образом, удачно влив крупную сумму перед периодом роста можно заметно улучшить доходность стратегии. И наоборот.
Учет инвестиций с помощью ЧИСТВНДОХ
Проблема функции ВСД в том, что она верна для периодических денежных потоков, поступающих и/или убывающих через равные промежутки времени. Однако понятно, что в реальных инвестициях ввод/вывод средств обычно происходит в спонтанном режиме. В этом случае для расчета доходности портфеля можно воспользоваться функцией ЧИСТВНДОХ.
Вся подобная статистика должна содержаться в брокерском отчете. Вычисления выполняются с помощью итерационного метода, подробное описание функции можно найти здесь.
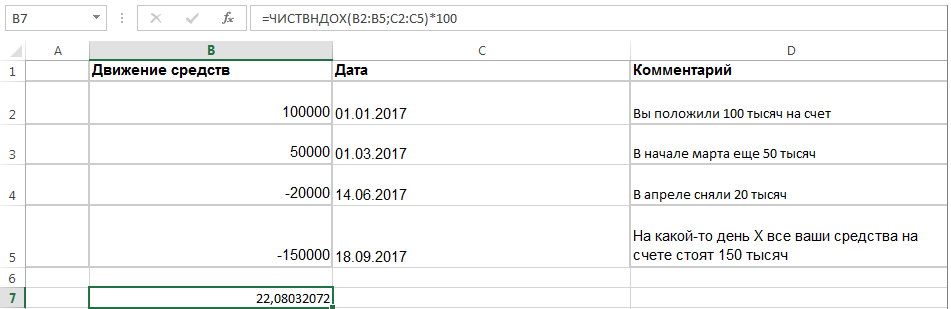
Основными в расчете являются две колонки: значений (введенных и выведенных средств) и соответствующих дат, когда происходил ввод или вывод денег. Обратите внимание, что общая стоимость активов указывается со знаком минус. После чего в произвольную ячейку, где требуется результат, нужно ставить следующую формулу:
В2:B5 — диапазон ячеек со значениями введенных или выведенных средств
С2:С5 — диапазон ячеек с датами, когда происходил ввод или вывод
Умножение на 100 позволяет получить результат в процентах. Для примера выше средняя годовая доходность будет ≈ 22.1%.
🔔 При инвестициях меньше года подобный расчет является некорректным. Кроме того, поскольку на рынке периодически возникают пузыри (доткомов на рынке США в 1995-2000 годах или российских активов на росте нефти в 2000-2008), а также бывают затяжные кризисы (обычно именно после пузырей — например Великая Депрессия 30-х или Япония после 1990 года), то для более адекватной оценки портфеля гораздо лучше подходят временные интервалы в несколько лет, чем за 1-2 года.
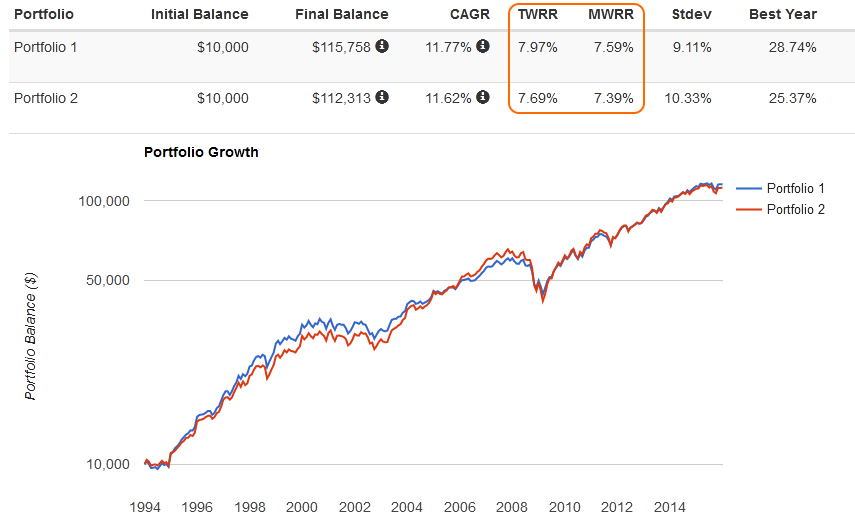
В заключении пример доходности инвестиционного портфеля одного моего клиента:
11 способов расчета доходности инвестиционного портфеля
Каждому инвестору, рано или поздно, приходится оценивать результаты своей инвестиционной деятельности или просто видеть значения полученной доходности в отчетах управляющего или брокерских приложениях.
И если вы сформировали портфель один раз и держите его без пополнения или изъятия средств, то подсчет итоговой доходности – простое дело. Но если вы регулярно проводите операции с портфелем, вносите и выводите деньги, то расчет итогового результата становится немного сложнее.
Например, считая доходность двумя разными способами, вы можете получить абсолютно разные результаты, вплоть до того, что при одном методе расчета ваша доходность будет положительной, а при другом отрицательной.
Два основных метода оценки доходности
Метод взвешивания по деньгам (MVR) показывает доходность со всеми изъятиями и пополнениями портфеля, в то время как метод взвешивания по времени (TWR), наоборот, показывает доходность, которую получил бы инвестор, если бы держал одну и ту же сумму, не пополняя счет и не изымая денег. Вследствие этого, доходность, рассчитанная разными способами, может значительно отличаться друг от друга.
Начальный пример
Для того, чтобы продемонстрировать разницу методов, рассмотрим следующую ситуацию:
В этом примере, как мы увидим ниже, инвестор потерял 7000 руб., несмотря на это, доходность, взвешенная по времени, будет положительной (+0,4%), а взвешенная по деньгам отразит реальные потери инвестора и будет отрицательной (-0,87%). И оба эти результата корректны!
Чтобы разобраться с тем, как такое возможно, рассмотрим 11 методов, с помощью которых исторически рассчитывалась доходность. Два из них широко применяются и сегодня, а один из этих двух методов является отраслевым стандартом в сфере управления инвестициями.
Методы, относящиеся к MWR (взвешенная по деньгам доходность)
1) Простой IRR (внутренняя норма доходности)
Простая внутренняя норма доходности, в случае использования для оценки доходности портфеля, подразумевает нахождение такого r, при котором выполняется следующее условие:
Также, в простом IRR есть допущение, что все денежные потоки произошли в середине анализируемого периода. Поэтому, чтобы сделать оценку более точной, нужно использовать модифицированный IRR.
2) Модифицированный IRR (MIRR)
Модифицированная внутренняя норма доходности отражает то же, что и простая IRR, но учитывает то, что каждый денежный поток происходит в разные промежутки анализируемого периода.
3) Простой метод Дитца
Простой метод Дитца является способом измерения доходности портфеля, который учитывает все денежные потоки в/из портфеля в течение периода.
Он основан на предположении, что все внешние потоки происходят в середине временного интервала (или равномерно распределены по всему периоду, и таким образом, потоки происходят в среднем в середине периода).
Ассоциация инвестиционных консультантов Америки (ICAA, 1971) предложила прямое расширение простого метода Дитца. Предполагается, что любой доход, полученный портфелем (например, дивиденды или купонные выплаты) будет недоступен для инвестиций управляющим портфелем и переносится на отдельный счет для выплаты непосредственно клиенту.
5) Модифицированный метод Дитца
Это способ измерения доходности портфеля, основанный, в отличие от простого метода Дитца, на взвешивании каждого денежного потока, поэтому считается более точным. Данный метод является наиболее точным среди MWR, а также распространенным среди управляющих портфелями.
Среди всех изложенных выше методов MWR, на сегодняшний день наиболее актуальным является Модифицированный метод Дитца. Все остальные методы являются менее точными и использовались управляющими в то время, когда точный моментальный подсчет доходности был затруднителен.
Методы, относящиеся к TWR (взвешенная по времени доходность)
6) TWR (Time-Weighted rate of return)
Взвешенная по времени доходность (TWR) — инвестиционный показатель, отражающий доходность портфеля, которая, в отличие от взвешенной по деньгам доходности (MWR), не зависит от изымания денег или пополнения портфеля, так как это не должно влиять на оценку эффективности работы управляющего портфелем (он, как правило, не может влиять на решения клиента внести и изъять деньги из упраления).
Вот формула для этого метода:
Методы, приближенные к TWR
Следующие 3 метода относятся к приближенным к TWR и могут иметь погрешность при расчёте, но позволяют очень быстро оценить примерную доходность.
7) Метод подстановки индекса
Процедура расчета взвешенной по времени доходности наиболее полно повторяет расчет доходности индекса и, следовательно, дает возможность использовать его в качестве бенчмарка. Поэтому, если точная оценка TWR недоступна, доходность бенчмарка (индекса) можно использовать для оценки стоимости портфеля на дату движения денежных средств.
Рассчитывается по формуле TWR, но доходность портфеля во время денежного потока оценивается по доходности бенчмарка (индекса).
Метод регрессии является более широким, нежели метод подстановки индекса, т.к. учитывает риск портфеля (бету).
Рассчитывается по формуле TWR, но доходность портфеля во время денежного потока оценивается по доходности бенчмарка (индекса), с корректировкой на риск портфеля (бету).
Рабочая группа Британского общества инвестиционных аналитиков (SIA, 1972) предложила ещё один метод, основываясь на своём обнаружении, что отношение MWR портфеля к условному фонду (или индексу) приблизительно соответствует отношению TWR портфеля к условному фонду (или индексу).
Гибридные методы
10) Метод BAI (или связанный IRR)
Институт банковского администрирования (BAI, 1968) предложил альтернативный гибридный подход, который, по сути, связывает простые внутренние нормы прибыли (IRR).
Для расчёта связанного IRR, перемножают доходности, рассчитанные по простому IRR за каждый период времени.
11) Связанный модифицированный метод Дитца
Альтернативой модифицированному методу Дитца является связывание модифицированных доходностей Дитца за более короткие периоды. Связанный модифицированный метод Дитца классифицируется как метод, взвешенный по времени, но, в отличие от истинного TWR, он не дает тех же результатов, т.к. TWR делает оценку непосредственно после каждого денежного потока.
Возвращаемся к примеру
Для того чтобы продемонстрировать разницу методов, вернемся к задаче, которую мы описывали выше:
Если мы рассчитаем доходность данного портфеля методами, описанными выше, то получим следующие результаты:
Как вы можете видеть из полученных результатов, доходность, рассчитанная разными способами, может демонстрировать совершенно разные результаты.
Данный пример демонстрирует не только разницу между доходностью, рассчитанную разными способами, но и то, что неправильный выбор времени для пополнения/изъятия денег из портфеля может отразиться на его доходности.
Выводы
Оба базовых метода расчёта доходности имеют свою ценность, и каждый из них следует использовать в разных ситуациях.
Файл с расчетами доходности по приведенному примеру всеми 11 способами можно скачать по этой ссылке (.xls)
Эта статья частично основана на материалах из книги Carl R. Bacon, Practical Portfolio Performance Measurement and Attribution.
Управляющая компания «ДОХОДЪ», Общество с ограниченной ответственностью (далее Компания) не обещает и не гарантирует доходность вложений. Решения принимаются инвестором самостоятельно. Информация, представленная здесь, не является индивидуальной инвестиционной рекомендацией, а упоминаемые финансовые инструменты могут не подходить вам по инвестиционным целям, допустимому риску, инвестиционному горизонту и прочим параметрам индивидуального инвестиционного профиля. При подготовке представленных материалов была использована информация из источников, которые, по мнению специалистов Компании, заслуживают доверия. При этом данная информация предназначена исключительно для информационных целей, не содержит рекомендаций и является выражением частного мнения специалистов аналитической службы Компании. Невзирая на осмотрительность, с которой специалисты Компании отнеслись к составлению этой страницы, Компания не дает никаких гарантий в отношении достоверности и полноты содержащейся здесь информации. Никто ни при каких обстоятельствах не должен рассматривать эту информацию в качестве предложения о заключении договора на рынке ценных бумаг или иного юридически обязывающего действия, как со стороны Компании, так и со стороны ее специалистов. Ни Компания, ни ее агенты, ни аффилированные лица не несут никакой ответственности за любые убытки или расходы, связанные прямо или косвенно с использованием этой информации. Данная информация, действительна на момент ее публикации, при этом Компания вправе в любой момент внести в информацию любые изменения. Компания, ее агенты, работники и аффилированные лица могут в некоторых случаях участвовать в операциях с ценными бумагами, упомянутыми выше, или вступать в отношения с эмитентами этих ценных бумаг. Результаты инвестирования в прошлом не определяют доходы в будущем, государство не гарантирует доходность инвестиций в ценные бумаги. Компания предупреждает, что операции с ценными бумагами связаны с различными рисками и требуют соответствующих знаний и опыта.
Правильный расчет доходности инвестиций
Сегодня хочу вам рассказать о том, как я рассчитываю доходность инвестиций. Это очень частый вопрос как в директе, так и в комментариях. Оно и понятно, я каждую неделю в своем блоге привожу доходность портфеля загадочным для многих методом TWR (Time-Weighted Return), вдобавок еще и в годовом выражении.
⠀
Смотрю на многих блогеров-инвесторов и порой становится смешно, от того, как они считают свою доходность, да к тому же выкладывают эту ч̶е̶п̶у̶х̶у̶ информацию на всеобщее обозрение.
⠀
По мне уж лучше сложно и непонятно, но зато правильно, чем легко и неправильно.
⠀
Что делают другие инвесторы-блогеры? Они просто делят свою прибыль к сумме инвестиций, упуская из виду тот факт, что у инвестиций есть временнАя стоимость или как я его называю «рабочее время».
⠀
Объясню на примере. Допустим, вы вложили 100 тыс. руб. 1 января 2019 г. под 10% годовых. 1 июля 2019 г. вы решили увеличить вклад еще на 100 тыс. руб., но под 5% годовых. Какая доходность инвестиций за 2019 год?
⠀
Кто сходу ответит на этот вопрос, поистине гений инвестирования и математики, т.к. посчитать реальную доходность этого простого примера не так легко, как кажется с первого взгляда.Ответ будет в конце, но сначала подумайте и предположите свой вариант, а потом напишите в комментарии, насколько точны вы оказались.
⠀
В этом примере (можете считать это подсказкой) первая инвестиция принесет доход 10 тыс. руб. за год, вторая инвестиция проработает лишь полгода и успеет принести 2,5 тыс. руб. (5% от 100 тыс. деленная на 2). Итого за год мы будем иметь 12,5 тыс. руб. прибыли при вложениях 200 тыс. руб.
⠀
Тут-то многие смогут предварительно рассчитать доходность: 12,5/200 * 100% = 6,25%! Так в принципе и считают, ничего не подозревая, другие блогеры и приложения для инвестиций. Но не радуйтесь, это неверный ответ! И вот почему.
⠀
Для того, чтобы верно рассчитать доходность, нужно учитывать стоимость инвестиций во времени В расчете выше, это не было учтено, и стоимость была взята 200 тыс. руб. Но вторая инвестиция проработала лишь полгода, поэтому ее вклад в доходность будет ниже.
Чтобы учесть этот фактор, нужно применить формулу средневзвешенной стоимости инвестиций:
V = (Т1 * нач + Т2 * (Sнач + Sвв) + ТЗ * (Sнач + Sвв — Sвыв) +… + Тn * (Sнач + суммSвв — суммSвыв)/ суммТ,
где V — средневзвешенная сумма вложенных средств;
Т1, Т2, ТЗ, Tn — количество дней в подпериоде (срок от первой до второй инвестиции, от второй до третьей ит.д.);
Sнач — сумма первоначальных инвестиций;
суммSвв — сумма всех вводов средств;
суммSвыв — сумма всех выводов средств;
суммТ — суммарное количество дней инвестирования.
Полученное значение подставляем в известную формулу(прибыль/инвестиции*100%):
Данная сложная формула позволяет посчитать доходность для определенного периода. Ее можно перевести в годовой эквивалент по следующей формуле:
V = (181*100 + 184*(100+100))/365 = 150 411 руб.
Мы получили нашу средневзвешенную стоимость инвестиций! Заметьте, она сильно отличается от 200 реально вложенных!
Теперь легко посчитать доходность:
12 500/150 411*100% = 8,31%!
Переводить доходность в годовой эквивалент, как вы можете догадаться, не имеет смысла, т.к. мы рассматривали инвестиции как раз за год. Для наглядности все равно рассчитаем:
Как вам разница между 6,25% и 8,31%? Стало лучше и доходность увеличилась! Если в портфеле убыток, то перекос будет в сторону увеличения убытка. Но это будут правдивые цифры!
Нужно сказать, что примерно таким же образом рассчитывают доходность в инвестиционных фондах (на минуточку).
И, кстати, приложения для инвестиций также считают неправильно, т.е. без учета временной стоимости инвестиций или, как я его окрестил, «рабочего времени». Поэтому я бы не советовал полагаться на их показатели.
Я для себя все эти формулы вбил в табличную форму Ехсеl, где все рассчитывается автоматически, нужно только вносить данные о пополнениях. Никаким иным способом я не считаю доходность, т.к., уверен, что данный метод самый точный и правильный.
Если интересно, подписывайся на мой быстрорастущий Instagram блог об инвестициях. Там информация для всех: от начинающих до продвинутых.
Ставка доходности, взвешенная по деньгам
Опубликовано 10.06.2020 · Обновлено 10.06.2021
Что такое Ставка доходности, взвешенная по деньгам?
Ставка доходности, взвешенная в денежном выражении (MWRR), является показателем эффективности инвестиций. MWRR рассчитывается путем нахождения нормы прибыли, которая устанавливает текущие значения всех денежных потоков, равные стоимости первоначальных инвестиций. MWRR эквивалентен внутренней норме доходности (IRR).
Ключевые моменты:
Понимание нормы прибыли, взвешенной по деньгам
Формула для MWRR Is
пVОзнак равнопVязнак равноCF0+CF1(1+ярр)+CF2(1+ярр)2+CF3(1+ярр)3+…CFп(1+ярр)пжчере:пVОзнак равноPV OutflowsпVязнак равноPV InflowsCF0знак равноЯпятялсычоутлуогянvEсектмент CF1,CF2,CF3,…CFпзнак равноCAсекч еложеNзнак равноEach periodяррзнак равноИнитиал рате оф ретурн\begin
How to Calculate the Money-Weighted Rate of Return
What Does the Money-Weighted Rate of Return Tell You?
There are many ways to measure asset returns, and it is important to know which method is being used when reviewing asset performance. The MWRR incorporates the size and timing of cash flows, so it is an effective measure of portfolio returns.
The MWRR sets the initial value of an investment to equal the future cash flows, such as dividends added, withdrawals, deposits, and sale proceeds. In other words, the MWRR helps determine the rate of return needed to start with the initial investment amount factoring all of the changes to cash flows during the investment period including the sale proceeds.
Cash Flows and the Money-Weighted Rate of Return
As stated earlier, the MWRR for an investment is identical in concept to the IRR. In other words, it is the discount rate on which the net present value (NPV) = 0, or the present value of inflows = present value of outflows.
It’s important to identify the cash flows in and out of a portfolio including the sale of the asset or investment. Some of the cash flows that an investor might have in a portfolio include:
Outflows
Inflows
Example of the Money-Weighted Rate of Return
Each inflow or outflow must be discounted back to the present using a rate (r) that will make PV (inflows) = PV (outflows).
Solving for r using a spreadsheet or financial calculator, we have an MWRR of 11.73%.
The Difference Between Money-Weighted Rate of Return and Time-Weighted Rate of Return
The money-weighted rate of return is often compared to the time-weighted rate of return (TWRR), but the two calculations have distinct differences. The TWRR is a measure of the compound rate of growth in a portfolio. The TWRR measure is often used to compare the returns of investment managers because it eliminates the distorting effects on growth rates created by inflows and outflows of money.
It can be difficult to determine how much money was earned on a portfolio because deposits and withdrawals distort the value of the return on the portfolio. Investors can’t simply subtract the beginning balance, after the initial deposit, from the ending balance since the ending balance reflects both the rate of return on the investments and any deposits or withdrawals during the time invested in the fund.
The TWRR breaks up the return on an investment portfolio into separate intervals based on whether money was added or withdrawn from the fund. The MWRR differs in that it takes into account investor behavior via the impact of fund inflows and outflows on performance but doesn’t separate the intervals where cash flows occurred like the TWRR. Therefore, cash outlays or inflows can impact the MWRR. If there are no cash flows, then both methods should deliver the same or similar results.
Limitations of Using Money-Weighted Rate of Return
The MWRR considers all the cash flows from the fund or contribution, including withdrawals. Should an investment extend over several quarters, for example, the MWRR lends more weight to the performance of the fund when it is at its largest. Hence, the description “money-weighted.”
The weighting can penalize fund managers because of cash flows over which they have no control. In other words, if an investor adds a large sum of money to a portfolio just before its performance rises, it equates to positive action. This is because the larger portfolio benefits more (in dollar terms) from the growth of the portfolio than if the contribution had not been made.
On the other hand, if an investor withdraws funds from a portfolio just prior to a surge in performance, it equates to a negative action. The now-smaller fund sees less benefit (in dollar terms) from the growth of the portfolio than if the withdrawal had not occurred.
Как считать индикаторы инвестиционной привлекательности активов
На примере портфеля Уоррена Баффетта
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
((1 + 20%) × (1 − 10%) × (1 + 30%)) 1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному : акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%) 1/4 = 15,8%.
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%) 1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность) (365 / Количество дней владения активом) − 1
(1 + 74%) (365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива) (1 / Количество периодов) − 1
((270 × 20 + 2 × 20) / 200 × 20) (1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как победить выгорание
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Правило трех сигм гласит, что практически все значения нормально распределенной случайной величины лежат в диапазоне трех стандартных отклонений от среднего арифметического значения случайной величины. Случайной величиной у нас выступает годовая доходность по акции
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.