машина тьюринга в игре жизнь

Машина тьюринга в игре жизнь

Наука. Величайшие теории. Выпуск 15: Размышления о думающих машинах. Тьюринг. Компьютерное исчисление

Наука. Величайшие теории Выпуск № 15, 2015 Еженедельное издание

Пер. с йен. — М.: Де Агостини, 2015. — 152 с.

© Rafael Lahoz-Beltra, 2012 (текст)

© RBA Collecionables S.A., 2012

© ООО «Де Агостини», 2014-2015

Несмотря на короткую жизнь, Алан Тьюринг — одна из самых влиятельных личностей XX века. Вот всего несколько вех его профессионального пути. Ученый разработал гипотетическую машину, получившую название машины Тьюринга, с помощью которой создал теоретические основы для реализации первых компьютеров, он стал автором одного из самых быстрых компьютеров той эпохи — Pilot АСЕ. Основным успехом Тьюринга как криптографа стала расшифровка кода «Энигмы» — шифровальной машины, которую немцы использовали во время Второй мировой войны. Кроме того, он стал первопроходцем, заложив основы исследований искусственного интеллекта и математической биологии.

Задача нашей книги — объяснить, не отступая от истины и при этом в доступной форме, сущность его фундаментального вклада в развитие современного мира.

Выполняя эту задачу, мы объединили в книге элементы развлекательной науки, а также биографические детали, показав, каким образом некоторые важнейшие открытия Алана Тьюринга стали частью нашей повседневной жизни. В числе вопросов, на которые наша книга дает ответ, — что такое компьютер? почему компьютеры зависают? в какой стране был изобретен компьютер? все ли виды задач могут решить компьютеры? что такое ката? что такое система оптического распознавания образов (OCR)? могут ли существовать разумные машины? как работает квантовый компьютер?

Разносторонний характер исследований Алана Тьюринга подчеркивает его гениальность. Способность ученого находить новые объекты для исследования, видеть связи между явлениями и вопросами, которые, на первый взгляд, могут показаться совершенно разными, позволяет его сравнить разве что с Джоном фон Нейманом. Именно с этими двумя именами связано появление в 1940-х годах понятия «междисциплинарный исследователь», то есть ученый, способный с использованием математики и компьютеров выделить общие элементы в биологии, экономике, социологии, физике с целью унификации, казалось бы, различных, но сходных но сути проблем.

Эта книга, раскрывающая Тьюринга как личность и как ученого, состоит из пяти глав. В главе 1, после описания его детства и юности до окончания учебы в Кембридже, подробно рассматривается одно из важнейших открытий — различные варианты машины Тьюринга, разработанные как самим британским гением, так и другими учеными, а также описываются попытки создания с помощью программного обеспечения машины Тьюринга или ее аналога. В конце главы мы остановимся на некоторых отдельных вопросах, среди которых — проблема остановки, объясняющая в том числе и почему компьютер «зависает».

Глава 2 описывает, как атаки немцев в годы Второй мировой войны привели британцев к созданию Блетчли-парка, в котором криптографы, включая Тьюринга, смогли расшифровать перехваченные сообщения Третьего рейха. В эти годы талант ученого полностью раскрылся, и он, как и многие его коллеги, получил достойные награды в конце войны. Именно в Блетчли-парке появился на свет Colossus («Колосс»), который считается первым в мире компьютером. Во Второй мировой войне люди гибли без счета, но также бессчетны и достижения человеческого разума в этот период. Напряженная работа, ставшая бесценным опытом, подготовила ученого к решающему шагу от абстрактного мира машины, носящей его имя, к созданию реального компьютера Pilot АСЕ («Туз»).

В главе 3 рассматривается вопрос, споры по которому не утихают по сей день: кто изобрел компьютер — британцы или американцы? Согласно принятой версии, ученые Соединенного Королевства благодаря разработке Colossus обеспечили своей стране первенство в создании компьютеров. Но почему же США сегодня занимают лидирующие позиции в этой индустрии?

После описания характеристик Pilot АСЕ и ответов на вышеупомянутые вопросы мы углубимся в архитектуру фон Неймана, то есть принцип, согласно которому компоненты компьютера работают на логическом и функциональном уровне, а закончим рассказом о том периоде, когда Алан Тьюринг посвятил себя программированию компьютеров в Манчестерском университете.

Уже в конце жизни Тьюринг увенчал свои исследования, возможно, самым амбициозным проектом и подготовил теоретическую базу для того, что сегодня называется искусственным интеллектом. Ученый продолжал работу в Манчестерском университете, задавшись глобальным вопросом: возможно ли существование разумной машины? Именно об этом рассказывается в главе 4. Тьюринг создал цепь искусственных нейронов и разработал тест, до сих применяемый для определения того, разумно ли ведет себя машина, например компьютер, когда играет в шахматы, переводит текст или выполняет другие задачи, для решения которых человек использовал бы свой разум.

В главе 5 детально рассматривается научное наследие Тьюринга. По очевидным причинам мы не говорим о современных компьютерах или суперкомпьютерах — ни о десктопах, ноутбуках, нетбуках или планшетах, ни об аппаратах, в основе которых лежит компьютер, таких как мобильный телефон, электронная записная книжка и другие. Все эти устройства являются результатом естественной эволюции теоретической машины Тьюринга и первых компьютеров — Colossus, ENIAC, Pilot АСЕ, EDSAC: все их версии можно перечислять бесконечно. В наследие Тьюринга можно включить не только сто вклад в развитие науки, гениальные находки и работы но информатике, но и все то, что было оставлено без завершения в его бумагах и вдохновило следующие поколения исследователей. Так, на стадии разработки находились квантовый компьютер, модели искусственных нейронных сетей и их использование в интеллектуальных системах в повседневной жизни, изучение молекулы ДНК с помощью компьютеров (структура ДНК была открыта Уотсоном и Криком за год до смерти Тьюринга).

Источник

Игра Жизнь. Её связь с машиной Тьюринга

Джон Конвей заинтересовался проблемой, предложенной в 1940-х годах известным математиком Джоном фон Нейманом, который пытался создать гипотетическую машину, которая может воспроизводить сама себя. Джону фон Нейману удалось создать математическую модель такой машины с очень сложными правилами. Конвей попытался упростить идеи, предложенные Нейманом, и в конце концов ему удалось создать правила, которые стали правилами игры «Жизнь». Впервые описание этой игры было опубликовано в октябрьском выпуске (1970) журнала Scientific American, в рубрике «Математические игры» Мартина Гарднера (Martin Gardner).

К настоящему времени более-менее сложилась следующая классификация фигур:

Планерное ружьё Госпера (англ.) — первая бесконечно растущая фигура

Райский сад

Райским садом (садом Эдема) называется такое расположение клеток, у которого не может быть предыдущего поколения. Практически для любой игры, состояние клеток в которой определяется несколькими соседями на предыдущем шаге, можно доказать существование садов Эдема, но построить конкретную фигуру гораздо сложнее.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_j записывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

В состав машины Тьюринга входит бесконечная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделённая на ячейки, и управляющее устройство, способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.

Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки ленты символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.

Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма

Билет 9 вопрос 1

OrCAD — пакет компьютерных программ, предназначенный для автоматизации проектирования электроники. Используется в основном для создания электронных версий печатных плат для производства печатных плат, а также для производства электронных схем и их моделирования.

Название OrCAD произведено от слов Oregon и CAD.

Продукты серии OrCAD принадлежат компании Cadence Design Systems. Последняя версия OrCAD имеет возможность по созданию и поддержке базы данных доступных интегральных схем. База данных может быть обновлена путём скачивания пакетов производителей компонентов, таких как Texas Instruments.

В составе пакета следующие модули:

§ Capture — редактор принципиальных схем,

§ Capture CIS Option — менеджер библиотек Active Parts,

§ PSpice Analog Digital — пакет аналого-цифрового моделирования,

§ PSpice Аdvanced Аnalysis — пакет параметрической оптимизации,

§ PSpice SLPS option — интерфейс связи с пакетом Matlab,

§ PCB Designer — редактор топологий печатных плат,

§ SPECCTRA for OrCAD — программа автоматической и интерактивной трассировки,

§ Signal Explorer — модуль анализа целостности сигналов и перекрестных искажений.

Билет 10 вопрос 1

В целом проектирование БИС в среде Cadence, реализуемое сегодня на платформе Virtuoso, включает этапы, изображенные на рисунке 2.4.

• системное проектирование – построение модели системы на высоком уровне абстракции с использованием языков программирования C/C++ и SystemC, разбиение на программные и аппаратные модули, исследование параметров системы, получение спецификаций (набора требуемых параметров) на программные и аппаратные блоки;

• аппаратное проектирование и верификация – разработка на основе спецификации поведенческих моделей отдельных блоков системы с использованием языков Verilog/VHDL, реализация проекта в базисе библиотек производителя ИС, проверка программно-аппаратной реализации на соответствие спецификациям, полученным на системном уровне;

Рисунок 2.4- Этапы проектирования БИС в среде Cadence

• физическое прототипирование – предварительное размещение элементов, оценка потребляемой мощности, планирование шин питания и иерархии тактовых сигналов, качественная оценка возможных искажений сигнала;

• проектирование и верификация топологии кристалла – разработка топологии заказных блоков, трассировка на уровне ячеек, проверка правил проектирования топологии, экстракция паразитных параметров.

Билет 11 вопрос 1

Казёнов страница 102

Билет 12 вопрос 1

ЕСТЬ И В КАЗЁНОВЕ

Билет 12 вопрос 2

Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). Вматематике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.

Формальное определение

n-местным (n-арным) отношением, заданным на множествах , называется подмножество прямого произведения этих множеств.

Иногда понятие отношения определяется только для частного случая для отношения R. Тогда факт принадлежности n-ки этому отношению можно записать как:

.

Арность

§ Одноместные отношения соответствуют свойствам или атрибутам.

§ Двуместные отношения называют бинарными и обычно записывают инфиксной записью: x R y. Примерами множеств с введёнными на них бинарными отношениями являются графы и частично упорядоченные множества.

§ Трёхместные отношения называют тернарными.

Примеры

§ Отношение равенства на множестве вещественных чисел — бинарное отношение, обозначаемое символом «=». Ему принадлежат все пары вида , и только они.

§ Отношение эквивалентности на произвольном множестве M — бинарное отношение, обычно обозначаемое символом «

». Состоит из пар вида , где x и y принадлежат одному классу эквивалентности, и только из них.

§ Отношение делимости на множестве натуральных чисел — бинарное отношение, обычно обозначаемое символом « | ». Состоит из пар вида , где x делит y нацело.

Отношения и предикаты

Отношение также может быть задано предикатом на n-й декартовой степени множества M: n-ка принадлежит отношению тогда и только тогда, когда предикат на ней возвращает значение 1 (или «истинно»). Таким образом, можно дать альтернативное определение отношения: если задано отображение 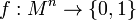, то отношением R называется прообраз единицы в f. Такое определение бывает полезно в информатике и математической логике.

Предикаты, которые формируются из отношений, заданных в соответствии с основным определением (когда множества в прямом произведении различны), используются в многосортном исчислении предикатов. [1]

Операции с отношениями

Система отношений, сформированная на одном и том же прямом произведении множеств, изоморфна алгебре множеств и допускает применение теоретико-множественных операций и проверок включения одного отношения в другое. Элементами множеств в этом случае являются кортежи элементов (n-ки).

Для отношений, у которых это ограничение не выполняется, теоретико-множественные операции не применимы, но возможны такие операции как соединение и композиция, которые используются в алгебре Кодда, алгебре кортежей и реляционной алгебре.

В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется непустое множество упорядоченных пар элементов этого множества.

Бинарные отношения могут обладать различными свойствами, такими как

§ Рефлексивность: .

§ Антирефлексивность (иррефлексивность): .

§ Симметричность: .

§ Антисимметричность: .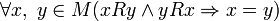

§ Транзитивность: .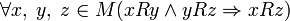

§ Асимметричность: . Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Виды отношений

§ Рефлексивное транзитивное отношение называется отношением квазипорядка.

§ Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.

§ Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.

§ Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.

§ Полное антисимметричное транзитивное отношение называется отношением линейного порядка.

§ Антирефлексивное асимметричное отношение называется отношением доминирования.

Операции над отношениями:

Так как отношения, заданные на фиксированной паре множеств A, B, суть подмножества множества , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных ,

Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.

Например, 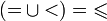, , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто.

Кроме перечисленных важное значение имеют ещё операции обращения и умножения отношений, определяемые следующим образом.

Пусть теперь , . Произведением отношений R, S называется отношение такое, что

Если , и , то произведение отношений не определено. Если же отношения рассматривать определённые на каком-то множестве A, то такой ситуации не возникает.

Например, рассмотрим отношение строгого порядка − 1 = I не всегда справедливо.

Имеют место следующие тождества:

§ ,

§ ,

§ ,

§ ,

§ .

Отметим, что аналоги последних двух тождеств для не имеют места.

Некоторые свойства отношения можно определить, используя операции над отношениями:

§ Рефлексивность: ,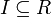

§ Симметричность: ,

§ Транзитивность: .

Источник

Julia и клеточные автоматы

Сегодня мы отправимся в красочное путешествие по миру клеточных автоматов, попутно изучая некоторые хитрые приемы их реализации, а также попытаемся понять, что скрывается за этой красотой — любопытная игра для праздного ума или глубокая философская концепция, находящая отклики во многих моделях.

Для практики и лучшего понимания следует попытаться самому реализовать приведенные ниже алгоритмы. Ну а если лень, или просто из интереса, можно поиграться с различными имплементациями:

Одномерный случай

Одномерный клеточный автомат представляет с собой отрезок разбитый на равные части — ячейки. Каждая ячейка может принимать одно из двух состояний, условно 0 или 1, черный или белый, живой или мертвый и т. д. Состояние каждой ячейки меняется по определенному правилу, учитывающему состояние соседей. Если принимать во внимание только ближайших соседей, то мы получим комбинацию из восьми состояний искомой ячейки и пары соседей. Каждой из этих комбинаций можно поставить в соответствие одно новое состояние для искомой ячейки, из чего следует общее количество правил равное 256 (количество 8-битных слов).

Чтобы надежно закрепить образ в своей нейросети, реализуем функцию визуализирующую одномерные клеточные автоматы.

Для начала следует установить и подгрузить все необходимые пакеты:

Правила для одномерных клеточных автоматов выражают числами от 0 до 255 (десятичные представления восьмибитных слов). Значит наша функция должна уметь представлять номер правила в двоичном виде, и составлять для него паттерн. Затем, при наивной реализации, происходит проход по всем ячейкам с заменой состояний:

Это правило 30, одно из любимых Стивена Вольфрама. Он, кстати, назначил денежные призы за решения задач связанных с этим правилом. Действительно, в этом что-то есть: периодичность граничащая с хаосом, плюс спонтанное зарождение упорядоченных структур… Но лично меня зацепили треугольники Серпинского, которые часто встречаются здесь и там. А для одномерных КА они довольно частое явление:

В кругах и в цвете

Приверженцам объектно ориентированного программирования можно предложить вариант, где клеточный автомат выполнен в виде структуры. В этом случае будет удобно реализовать варьирование цвета и даже круглые поля:

Визуализация выполнена с помощью пакета Luxor, который мы разбирали ранее.

Игра в жизнь

«Жизнь» Конвея — самый популярный из двумерных (да и трехмерных) клеточных автоматов. Эта модель отдаленно напоминает копошение бактерий в чашке Петри, и обладая Тьюринг полнотой, может послужить основой для чего угодно: моделирования мышления, компьютеров (архитектуры тетриса) и самой себя.

играбельно

Множество энтузиастов находят все новые структуры: осцилляторы, глайдеры, корабли (на гусеничном ходу!) и фабрики. То есть, вся прелесть здесь заключается в том, что на основе простых правил можно создавать сложные структуры, откуда возникает соблазн попытаться распространить данную модель на фундаментальные законы Естества. В частности С. Вольфрам балует нас подобными высказываниями. Вопрос, на сколько это правдоподобно и, главное, полезно, всегда вызывает споры, так что, не будем на нем заостряться. Лучше реализуем «Жизнь» использующую преобразования Фурье.

Жизнь без Фурье и не жизнь вовсе

Тем, кто занимался обработкой изображений, работа с БПФ в таком аспекте должна быть знакома. Остальным можно посоветовать попробовать заняться обработкой изображений, так как это очень интересно, и снабдит вас полезными абстракциями для понимания линейной алгебры.

За основу использовался алгоритм из хабровской статьи

Приятные бонусы этого подхода — это сравнительно быстрая отработка БПФ в силу его отполированности, и закольцованность граничных условий (действо происходит как бы на поверхности тора). Собственно, теперь можно обобщить «жизнь» непрерывным случаем.

Гладкая жизнь

Вот так в общем виде выглядит модель:

Состояние теперь описывается не 1 и 0, а сигмоидой, соседи учитываются в некотором радиусе, а еще понадобится решать дифуры.

В модели много свободных параметров, а также можно поиграться с разными методами для дифуров. В общем, есть простор для исследований. Также анимации всегда можно украсить шейдерами.

Тьюрмиты

Еще один интересный вид машин Тьюринга это тьюрмиты — клеточные автоматы, состояние которых определяется неким агентом, который будет перемещаться по полю в зависимости от этих самых состояний. Наиболее известный представитель этого вида — муравей Лэнгтона.

На клеточное поле, каждая ячейка которого может быть либо черной либо белой, сажается мураш, который будет действовать по следующему алгоритму:

На rosetta code есть довольно хитрая реализация, где направление муравья задается комплексным числом:

Поначалу, поведение агента кажется хаотичным. Но потом появляется магистраль — система выходит на стационар. Прекраснейший пример рождения порядка из кажимого хаоса!

Но самый смак начинается если расширить состояние ячейки за пределы одного бита:

Послойными наращиваниями получаем симметричную структуру, похожую на мозг! Для некоторых цветовых схем получается довольно футуристично

и еще ряд интересных правил:

Магистрали довольно частое явление

Мозг в ящике — довольно стабильная структура. Здесь результат тридцати миллиардов шагов:

Короче, с такого рода экспериментами можно засесть надолго. И это мы только комбинировали два направления (лево-право), а ведь можно добавить еще вперед-назад, к тому же, никто не говорил, что муравей обязан продвигаться на одну клетку! Держу пари, что такого рода расширение стандартных правил породит еще много интересных закономерностей!

Эпилог

К слову о жизни. Немало интереса вызывают самовоспроизводящиеся структуры, а ля циклы Лэнгтона

Можно почитать статью, где данную модель расширяют наличием пола и передачей генов. (Тут уж передаю эстафету кому-нибудь другому. Очень хотелось бы посмотреть на реализацию подобной штуки)

Тема клеточных автоматов с ростом вычислительных мощностей и улучшением алгоритмов становится все популярней. У Вольфрама в блоге небольшой отчет по этой теме, да и каждый может сам убедиться — статей много, причем самых разнообразных: там вам и дружба с нейронными сетями, и генераторы случайных чисел, и квантовые точки, и сжатие и много всякого другого.

Ну и напоследок самокопирующаяся структура созданная Тэдом Коддом на спор за пинту пива

Источник