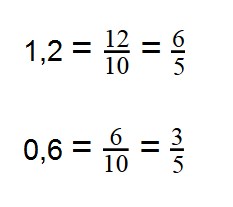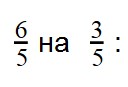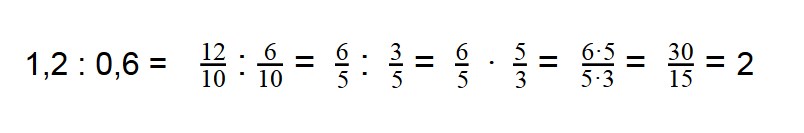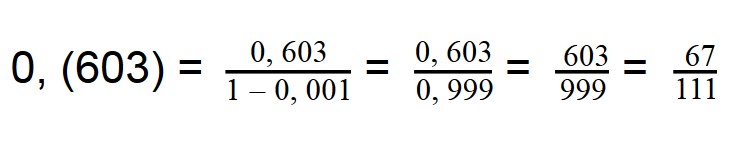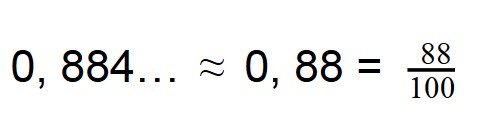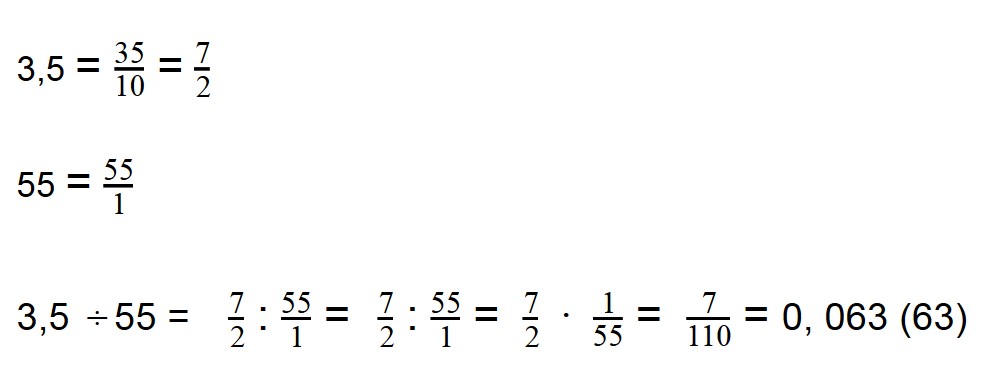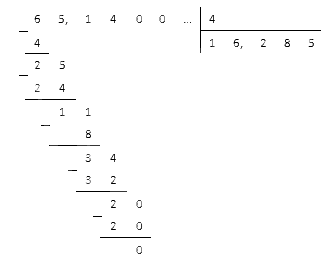Что значит разделить десятичную дробь на натуральное число
Деление десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основы деления десятичных дробей
Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.
Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.
Рассмотрим пример: разделите 1,2 на 0,6
Как решаем
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Таким образом, нам надо разделить
Ответ: 1,2÷0,6 = 2
Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.
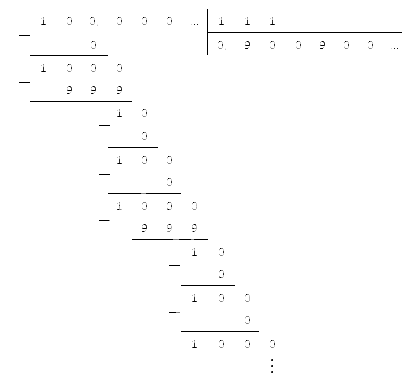
Периодические переводим в обыкновенную:
Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:
Как разделить целое число на десятичную дробь и наоборот
Здесь всё просто: приводим десятичную дробь к стандартному виду и натуральное число тоже представляем в виде дроби — само число нужно поделить на единицу.
Пример: 3,5 поделить на 55
Как решаем
Ответ: 3,5÷55 = 0,063 (63)
Как разделить десятичную дробь на натуральное число столбиком
Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.
Пример: Разделить столбиком 49,14÷3
Как решаем
1. Делим столбиком, предварительно дописав два нуля к десятичной дроби.
2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части
В конце у нас нулевой остаток, значит деление завершено.
Ответ: 49,14÷3 = 16,38
Как разделить столбиком одну десятичную дробь на другую
Все просто: умножаем делимое и делитель на 10, 100 и так далее — так, чтобы делитель превратился в натуральное число. А потом решаем также, как в примере выше:
1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Пример: поделить столбиком 63,42 на 2,1
Как решаем
Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21.
Затем производим деление
Ответ: 63,42÷2,1 = 30,2
Как разделить десятичные дроби на 1000, 100, 10 и другие
Как вы уже заметили, есть основное правило деления десятичных дробей: по нему деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и другие.
Чтобы выполнить действие, нужно просто перенести запятую влево на нужное количество цифр (равное нулям). Если значений в числе не хватит для переноса — дописываем нужное количество нулей:
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
Правило из предыдущего пункта поможет нам без труда разделить дроби на указанные значения. Переводим эти числа в стандартные дроби и затем при делении действие будет аналогично умножению на 1000, 100, 10 (так как дробь, на которую делим переворачивается).
Чтобы найти ответ в подобных задачах, мы переносим запятую на одну, две, три цифры вправо (в зависимости от числа, на которое делим) и дописываем нули, если цифр в числе окажется недостаточно.
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Вот как поступим со смешанным числом: записываем его в виде неправильной дроби, десятичную — в виде обычной дроби и делим по уже стандартной схеме.
Как правильно делить десятичные дроби на натуральное число
Деление десятичной дроби на натуральное число
Десятичная дробь — такая дробь, которая имеет знаменатель в виде степени числа 10.
Запись десятичной дроби подразумевает отсутствие знаменателей. Если дробь правильная, то ее целая часть равна нулю. Целую часть в десятичной дроби отделяют с помощью запятой от числителя.
Деление десятичной дроби на натуральное число предусматривает деление дроби на заданное число без учета запятой. Для того чтобы получить верный ответ, исключенная запятая дописывается в частном после целой части по окончании деления.
В итоге получается дробь, являющаяся конечной или бесконечной периодической десятичной дробью. Результат определяется остатком. В том случае, когда остаток нулевой, результат деления будет конечным. При повторе остатков получается периодическая дробь.
В качестве примера для закрепления материала, который изучают в средних классах, попробуем разделить десятичную дробь 49,14 на натуральное число 3. В первую очередь следует дописать пару нулей к десятичной дроби и выполнить деление в столбик. Результатом деления целой части дроби будет число 16. Выделим данный ответ с помощью запятой и продолжим вычисления в дробной части. Получив в итоге нулевой остаток, можно завершить деление:
Делим десятичные дроби на 1000, 100, 10: как это сделать правильно
Таким образом, для выполнения расчетов потребуется перенос запятой в левую сторону на необходимое количество цифр, которое равно нулям. В том случае, когда значений в числе недостаточно, чтобы перенести, следует расставить нужное число нулей. К примеру:
0,42 ÷ 10000 = 0,000042
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие
В предыдущем разделе было рассмотрено правило, которое пригодится для деления десятичных дробей на 0,001, 0,01, 0,1 и другие значения. Достаточно выполнить перевод этих самостоятельных чисел в вид стандартных дробей. Дальнейшие действия будут такими же, как в случае умножения на 100, 100, 10. Это объясняется переворотом дроби, на которую выполняется деление.
При решении подобных заданий следует перенести запятую на одну, две, три цифры в правую сторону. Здесь количество значений определяется числом, на которое нужно выполнить деление. Затем необходимо дописать нули в том случае, когда не хватает цифр в числе. Например:
Пояснения на примерах
Используя правило деления десятичных дробей, решить сложное выражение:
Выполним работу по делению всех компонентов уравнения отдельно, следуя стандартному алгоритму деления десятичной дроби на натуральное число. Получим:
Запишем полученные ответы в выражение и вычислим результат:
С помощью деления десятичной дроби на число 6 преобразуем выражение:
Определить значение х:
Руководствуясь правилом деления десятичной дроби, выполним вычисления:
При делении десятичной дроби получим:
Урожайность на первом участке составит:
17388 ÷ 41400=0,42 ( к г / м 2 )
На втором участке урожайность составила:
0,42 + 0,07 = 0,49 ( к г / м 2 )
Вычислим объем зерна, собранный на втором участке:
40200 × 0,49 = 19698 (кг)
Определим разницу в объемах урожая между первым и вторым участками:
19698 – 17388 = 2310 (кг)
Ответ: урожай второго участка равен 19698 кг, это на 2310 кг больше, чем собрано на первом участке.
Пять машин с песком и три машины со щебнем весят 22,8 т. Требуется определить массу одной машины, загруженной щебнем, когда одна машина с песком весит 2,7 т.
Вес пяти машин с песком составит:
Три машины, загруженные щебнем, имеют общую массу:
Одна машина со щебнем весит соответственно:
Ответ: одна машина со щебнем весит 3,1 т.
Последовательно выполним деление десятичных дробей:
Деление десятичных дробей: правила, примеры, решения
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Точность результата будет зависеть от степени округления.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Решение
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Решение
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Деление десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, как десятичную дробь можно разделить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления изложенного материала.
Деление десятичной дроби на натуральное число
Делитель – 10, 100, 1000, 10000 и т.д.
Чтобы разделить десятичную дробь на натуральное число 10, 100, 1000, 10000 и т.д., выполняем перенос десятичного разделителя (запятой) влево на столько позиций, сколько нулей содержит делитель.
Пример 1
Объяснение: В числе 10 всего один ноль, значит запятую сдвигаем на одну позицию влево.
Пример 2
Объяснение: В числе 100 два нуля, значит запятую сдвигаем на две позиции.
Примечание: если количество нулей в делителе больше количества цифр в целой части делимого, значит отсчитываем столько позиций, сколько позволяет дробь, затем дописываем оставшееся количество нулей слева, ставим запятую и добавляем ноль в целой части новой десятичной дроби.
Пример 3
62,75 : 1000 = 0,06275
Объяснение: Т.к. в числе 1000 три нуля, отсчитываем две позиции влево, добавляем оставшийся ноль с левой стороны, пишем запятую и затем – ноль в целой части полученной дроби.
Делитель – любое число
Чтобы разделить десятичную дробь на любое натуральное целое число:
Пример 4: разделим дробь 12,516 на 3.
Пример 5: разделим дробь 3,726 на 15.
Т.к. целая часть исходной дроби меньше делителя, значит целая часть частного равняется 0 (т.е. пишем ноль, ставим запятую и продолжаем выполнять деление).
Деление десятичной дроби на другую десятичную дробь
Чтобы разделить одну десятичную дробь на другую, умножаем обе дроби на такое число (10, 100, 1000 и т.д.), чтобы они стали целыми числами (количество нулей у множителя зависит от наибольшего количества цифр после запятой у той или иной дроби). Затем находим частное.
Примечание: этот же прием можно применять, чтобы разделить десятичную дробь на целое число.
Пример 6: найдем, сколько будет 5,468 делить на 3,2.
У дроби 5,468 три цифры после запятой, а у 3,2 – всего одна. Значит их обе умножаем на 1000, затем находим требуемый результат.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.