Что значит пропорциональные отрезки

Пропорциональные отрезки

Отрезки AB и CD пропорциональны отрезкам AB₁ и CD₁, если:

Отношением отрезков AB и CD называется отношение их длин, т.е. \( \frac . \)

Пример 1. На рисунке 1 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).

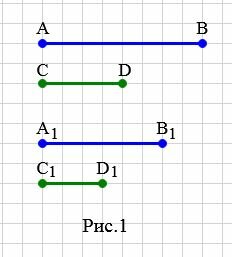Решение. Запишем длины отрезков:

.

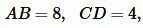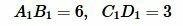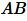
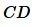
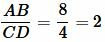Отношение отрезков и равно:

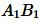
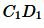
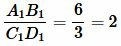Отношение отрезков и равно:

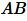
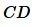
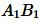
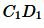
значит отрезки и пропорциональны отрезкам и .

Легко убедится, что выполяется также равенство (2) (это следует также из правила перекрестного умножения):

, .

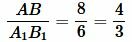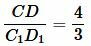Пример 2. На рисунке 2 заданы отрезки \( \small AB, \; CD, \; A_1B_1,\; C_1D_1. \) Определить, являются ли отрезки \( \small AB \) и \( \small CD \) пропорциональны отрезкам \( \small A_1B_1 \) и \( \small C_1D_1 \).

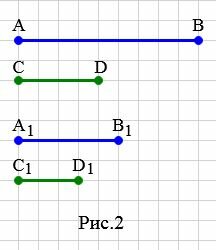Решение. Запишем длины отрезков:

.

, .

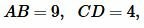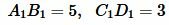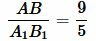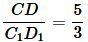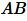
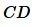
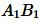
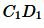
Следовательно отрезки и не пропорциональны отрезкам и .

Источник

Пропорциональные отрезки

Всего получено оценок: 311.

Всего получено оценок: 311.

Пропорциональные отрезки очень важны для определения подобия фигур. К тому же, правильно нареченные пропорционально рисунки помогают в правильном решении математических задач. Именно поэтому так важно разбираться в данной тематике.

Определение

Пропорциональными отрезками называются отрезки, у которых имеется постоянный коэффициент пропорциональности. Под коэффициентом пропорциональности понимается отношение длин отрезков.

Рис. 1. Пропорциональные отрезки.

Согласно определению пропорциональных отрезков, два отрезка всегда пропорциональны между собой, поскольку их длины не меняются со временем. Значит, не меняется и коэффициент пропорциональности.

Несмотря на это, чаще всего под пропорциональными отрезками понимают отрезки с коэффициентом кратным 0,5. Например, отрезки с коэффициентом 2,5, 1,5, 2 и тому подобные.

Пропорциональными будут являться и отрезки, составляющие подобные фигуры. Это действует в обе стороны. Если фигуры подобны, то их стороны пропорциональны, если все стороны пропорциональны, то фигуры подобны.

Подобные фигуры

Нужно понимать, что подобными фигурами могут быть не только треугольники, но вообще любые фигуры в геометрии, если все углы этих фигур равны, а длины сторон пропорциональны.

Рис. 2. Подобные фигуры.

Но при этом признаки подобия существуют только для треугольников. Их всего 3:

Пропорциональными могут быть только отрезки, как объекты имеющие длину. Прямая или луч бесконечны, а потому не могут быть подобными.

Пример

Решим небольшую задачу на пропорциональность отрезков. Имеется 3 пропорциональных отрезка. Каждый из которых больше предыдущего. Первый отрезок равен 5, третий 20. Необходимо найти длину второго отрезка.

Отрезки пропорциональны, значит отношение больших к меньшим будет постоянным. Обозначим неизвестны отрезок за х и решим уравнение.

Перенесем выражение из правой части в левую. Приведем получившееся выражение под один знаменатель и решим дробно-рациональное уравнение.

Что мы узнали?

Мы узнали, что такое пропорциональные отрезки. Выделили области, где могут быть применены навыки обращения с пропорциональными длинами и привели пример на заданную тему.

Источник

Пропорциональные отрезки

Отношением отрезков AB и CD называется отношение их длин, то есть .

Говорят, что отрезки AB и СD пропорциональны отрезкам и , если

.

Например, отрезки AB и CD, длины которых равны 2 и 1 см, пропорциональны отрезкам и , длины которых равны 3 см и 1.5 см. В самом деле, .

Понятие пропорциональности аналогичным образом вводится и для большего числа отрезков:

Понятие пропорциональных отрезков используется в теореме Фалеса, а также в аффинной геометрии.

См. также

Полезное

Смотреть что такое «Пропорциональные отрезки» в других словарях:

Теорема Фалеса — Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему. Теорема Фалеса одна из теорем планиметрии. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести… … Википедия

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Трапеция — У этого термина существуют и другие значения, см. Трапеция (значения). Трапеция (от др. греч. τραπέζιον «столик»; … Википедия

ЕВКЛИД — [греч. Εὐκλείδες] (кон. IV нач. III в. до Р. Х.), древнегреч. математик и педагог, представитель александрийской математической школы, широкую известность приобрел благодаря сочинению по основам математики, озаглавленному «Начала» (Στοιχεῖα, букв … Православная энциклопедия

ДИАГРАММА — ДИАГРАММА, наиболее распространенная форма графических изображений (см.), состоящая в том, что для выражения тех или иных количественных свойств явлений или для выражения закономерностей, установленных при помощи статистики, пользуются различными … Большая медицинская энциклопедия

КРИСТАЛЛЫ — (от греч. crystallos лед), однородные твердые тела, которые имеют закономерное внутреннее строение. Схемой такого строения является так называемая пространственная решот ка (см. рисунок), которую надо понимать как геометрический образ… … Большая медицинская энциклопедия

Биссектриса — (от лат. bis дважды и seco рассекаю) угла, прямая, проходящая через вершину угла и делящая его пополам. Б. треугольника отрезок Б. одного из углов треугольника от вершины угла до пересечения с противоположной стороной. Б. делит… … Большая советская энциклопедия

ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… … Физическая энциклопедия

Источник

Прямая и обратная пропорциональность

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

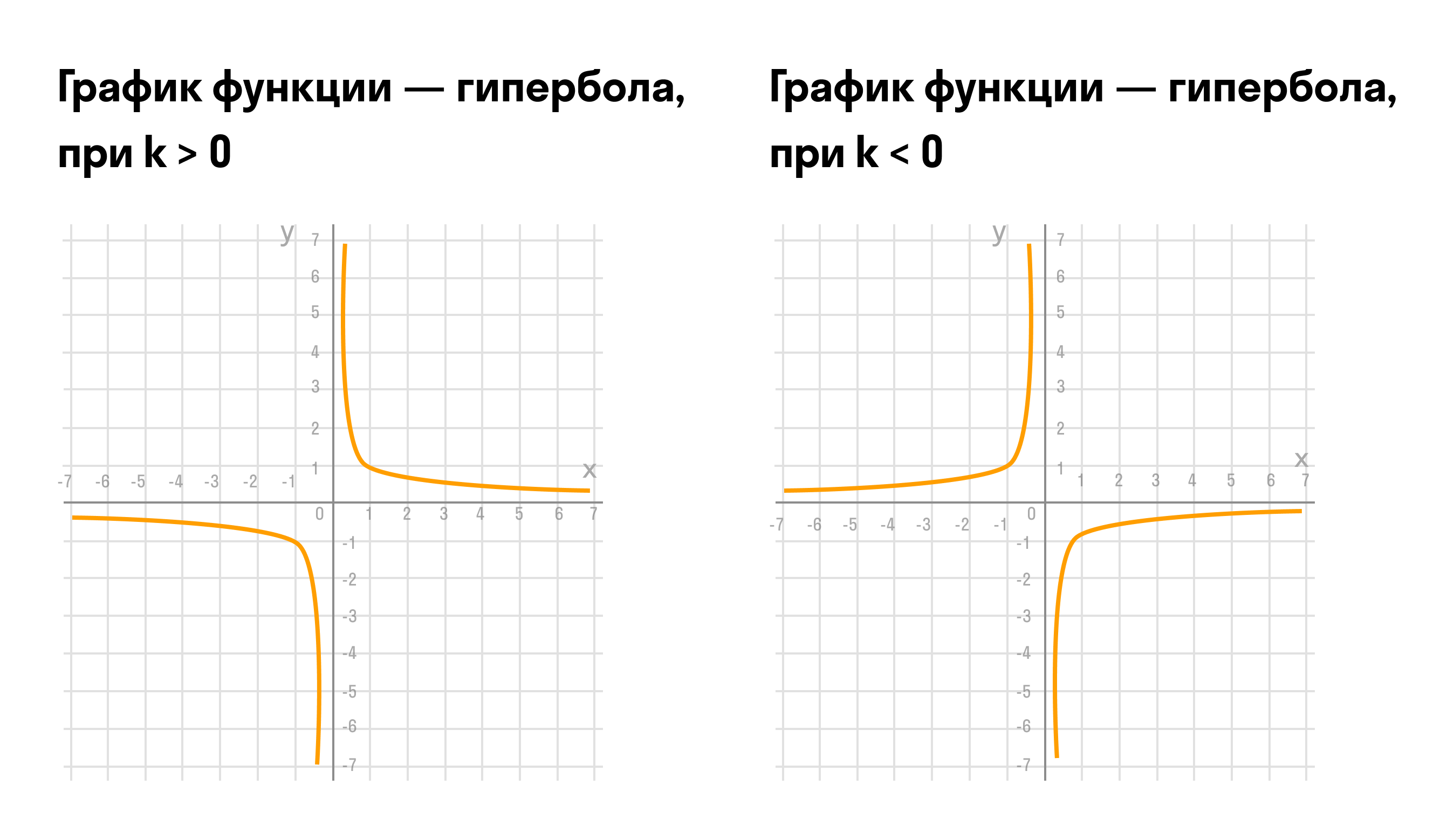
Графиком обратно пропорциональной зависимости величин является гипербола.

Свойства функции обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

Пропорциональные отрезки

Вокруг нас немало предметов, которые имеют одинаковую D форму, но разные размеры. Самый простой пример — большой и маленький мячи. В геометрии фигуры одинаковой формы называются подобными. Данная глава посвящена изучению подобных треугольников и признаков их подобия. Эти признаки широко используются в геометрии, в частности с их помощью будет доказано утверждение, сформулированное ещё при изучении геометрии в 7 классе: медианы треугольника пересекаются в одной точке. Кроме того, будет рассказано об использовании свойств подобных треугольников при проведении измерительных работ на местности.

Отношением отрезков АВ и CD называется отношение их длин, т. е.

Говорят, что отрезки АВ и CD пропорциинальны отрезкам А₁В₁ и C₁D₁, если

Например, отрезки АВ и CD, длины которых равны 2 см и 1 см, пропорциональны отрезкам А₁В₁ и C₁D₁, длины которых равны 3 см и 1,5 см. В самом деле,

Понятие пропорциональности вводится и для большего числа отрезков. Так, например, три отрезка АВ, CD и EF пропорциональны трём отрезкам А₁В₁ С₁D₁, и E₁F₁, если справедливо равенство

Источник