Что значит произвольные числа
Что такое произвольное число?
Что такое произвольное число?
Перевод произвольных чисел, т.
Е. чисел, содержащих целую и дробную части, осуществляется в два этапа.
Отдельно переводится целая часть, отдельно — дробная.
В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Р вопрос по математике.
Что такое произвольные функции?
Что такое произвольные функции.
Число записано с помощью трехсот единиц и произвольного количества нулей, может ли оно быть квадратом натурального числа?
Число записано с помощью трехсот единиц и произвольного количества нулей, может ли оно быть квадратом натурального числа?
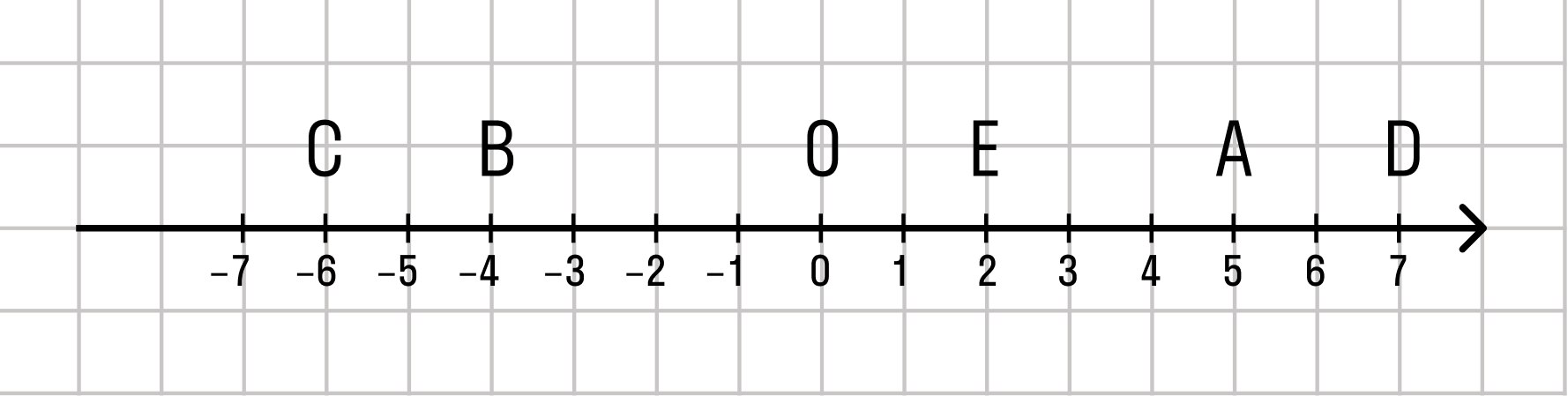
Изобразите на координатной плоскости все точки (x ; y) такие, что x = 5, y – произвольное число?
Изобразите на координатной плоскости все точки (x ; y) такие, что x = 5, y – произвольное число.
Что такое произвольный треугольник?
Что такое произвольный треугольник.
Натуральное число можно умножать на два и произвольным образом переставлять в нем цифры (запрещается лишь ставить ноль на первое место)?
Натуральное число можно умножать на два и произвольным образом переставлять в нем цифры (запрещается лишь ставить ноль на первое место).
Докажите, что превратить число 1 в число 8412 с помощью таких операций невозможно.
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры( нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры( нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 74?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры (нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры (нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 74?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры ( нельзя только ставить нуль на первое место)?
С числами можно выполнять следующие операции : умножать на два или произвольным образом переставлять цифры ( нельзя только ставить нуль на первое место).
Можно ли с помощью таких операций из 1 получить 78?
Действительные числа: определение, примеры, представления
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Данное определение можно записать иначе с учетом следующего:
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Действительные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение действительных чисел
Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —
Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —
Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:
Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.
Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.
Примеры действительных чисел:
Число нуль также является действительным числом, так как 0 — рациональное число.
Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.
При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.
Действительные числа на координатной прямой
Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Интересный факт: действительные числа заполняют каждую точку координатной прямой.
Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.
Представления действительных чисел
По определению действительными числами являются:
Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.
Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений
будут действительные числа.
Сравнение действительных чисел
Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:
Числовые и буквенные выражения. Формулы
Так же, как и у нашего языка общения есть алфавит и знаки-помощники (точка, тире, запятая и т.д.), математический язык вычисления также имеет свой алфавит:
Буквы и цифры в математике служат для обозначения чисел.
Цифрами обозначается конкретное, какое-то определённое число.
Буквами – любое или неизвестное число, в зависимости от задачи.
МАТЕМАТИЧЕСКИЕ ВЫРАЖЕНИЯ – это «слова» и «фразы» математики, записи, в которых содержатся:
При этом знаки математических действий и вспомогательные знаки ОБЯЗАТЕЛЬНО связывают числа и обозначают последовательность действий над ними.
Примеры математических выражений:
ВНИМАНИЕ!
НЕ ЯВЛЯЕТСЯ математическим выражением:
Например, это НЕ математические выражения:
Случаи опускания знака умножения в выражениях
В буквенных выражениях обычно знак умножения пишут только между числами, которые выражены цифрами.
В остальных случаях знак умножения опускают, например:
Как читать математические выражения
Простейшие математические выражения, состоящие из одного математического действия, называются по названию результата этого действия:
Более сложные выражения, называют по последнему выполняемому действию:
Важно не только уметь читать готовые математические выражения, но и «переводить» слова на математический язык – язык чисел, знаков действия и других символов:
Алгоритм чтения математических выражений
Чтобы прочитать математическое выражение, нужно:
При чтении сложного выражения повторяем действия алгоритма столько раз, сколько необходимо.
Формулы
Используя математические выражения можно одну величину представить в виде другой, то есть, установить зависимость значения одной величины от значения другой величины.
Велосипедист едет со скоростью \(v_<1>\) км/ч. Найти скорость:
а) автомобиля, если известно, что он едет в 3 раза быстрее: \(v_=3\cdot v_<1>\);
б) пешехода, если известно, что он двигается на 15 км/ч медленнее: \(v_
= v_<1>-15\).
Иначе это называется выразить одну величину через другую.
Многие величины в математике имеют свои собственные обозначения. Например: S – площадь фигуры, P – периметр, t – время и т.д.
Запись такого равенства называется формулой.
ФОРМУЛА – это запись зависимости значения некоторой величины от значений одной или нескольких других величин. Или другими словами, это запись правила вычисления одной неизвестной величины при помощи известных других.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 3.3 / 5. Количество оценок: 8
Перевод произвольных чисел
Перевод дробных чисел из одной системы счисления в другую
Можно сформулировать алгоритм перевода правильной дроби с основанием p в дробь с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления числа.
3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример 2.17. Перевести число 0,6562510 в восьмеричную систему счисления.
Пример 2.17. Перевести число 0,6562510 в шестнадцатеричную систему счисления.
Пример 2.18. Перевести десятичную дробь 0,562510 в двоичную систему счисления.
| 0, | x 2 |
| x 2 | |
| x 2 | |
| x 2 |
Пример 2.19. Перевести в двоичную систему счисления десятичную дробь 0.710.
| 0, | x2 |
| x2 | |
| x2 | |
| x2 |
Очевидно, что этот процесс может продолжаться бесконечно, давая все новые и новые знаки в изображении двоичного эквивалента числа 0,710. Так, за четыре шага мы получаем число 0,10112, а за семь шагов число 0,10110012, которое является более точным представлением числа 0,710 в двоичной системе счисления, и т.д. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа.
Перевод произвольных чисел
Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Пример 2.20. Перевести число 17,2510 в двоичную систему счисления.
| Переводим целую часть: | Переводим дробную часть: |
| 17 2 1 8 2 0 4 2 0 2 2 0 1 | 0, 25 x2 0 50 x2 1 00 |
Пример 2.21. Перевести число 124,2510 в восьмеричную систему.
| Переводим целую часть: | Переводим дробную часть: |
| 124 8 4 15 8 7 1 | 0, 25 x8 2 00 |
2.3.4. Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2 n и обратно
1. Двоичное число разбить справа налево на группы по n цифр в каждой.
2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.
Пример 2.22. Число 1011000010001100102 переведем в восьмеричную систему счисления.
Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 5410628.
Пример 2.23. Число 10000000001111100001112 переведем в шестнадцатеричную систему счисления.
Разбиваем число справа налево на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 200F8716.
1. Двоичное число разбить слева направо на группы по n цифр в каждой.
2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов.
Пример 2.24. Число 0,101100012 переведем в восьмеричную систему счисления.
Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 0,5428.
Пример 2.25. Число 0,1000000000112 переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 0,80316
1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой.
2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов;
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2 n
Пример 2.26. Число 111100101,01112 переведем в восьмеричную систему счисления.
Разбиваем целую и дробную части числа на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 745,348.
Пример 2.27.Число 11101001000,110100102 переведем в шестнадцатеричную систему счисления.
Разбиваем целую и дробную части числа на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 748,D216.
Пример 2.28. Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления.
В соответствии с алгоритмом:
Задания для самостоятельного выполнения (Ответы)
2.38. Заполните таблицу, в каждой строке которой одно и то же целое число должно быть записано в различных системах счисления.
| Двоичная | Восьмеричная | Десятичная | Шестнадцатеричная |
| 9B |
2.39. Заполните таблицу, в каждой строке которой одно и то же дробное число должно быть записано в различных системах счисления.
| Двоичная | Восьмеричная | Десятичная | Шестнадцатеричная |
| 0,101 | |||
| 0,6 | |||
| 0,125 | |||
| 0,4 |
2.40. Заполните таблицу, в каждой строке которой одно и то же произвольное число (число может содержать как целую, так и дробную часть) должно быть записано в различных системах счисления.