Что значит прочитать график функции

Урок «Изучение графика числовых функций»

Краткое описание документа:

Каждый старший школьник должен уметь читать графики числовых функций. Такие навыки начинают отрабатываться с момента знакомства с графиками в курсе математики. К 10 классу эти умения должны получить достаточно устойчивый уровень. Хотя с самим понятием чтения графиков, в более глубоком смысле, обучающиеся знакомятся именно в 10 классе. И в помощь учителю, который собирается объяснять материал по данной теме, разработан данный видеоурок.

Здесь содержится полезная, полная и качественная информация, усвоение которой не затруднено ничем. Обучающиеся легко освоят материал по теме, так как он подобран в соответствии со рядом требований, в том числе по возрасту обучающихся.

Урок длится 5:32 минут. Практически столько же времени, если не отвлекаться на какие-то посторонние моменты, понадобится учителю, чтобы объяснить новый материал на уроке. Здесь же время строго регламентировано. Поэтому пока обучающиеся будут просматривать видеоурок, у них не будет времени отвлекаться, иначе они не поймут суть происходящего. Так с помощью данного урока можно сформировать у обучающихся такие качества, как внимательность, дисциплинированность и самостоятельность.

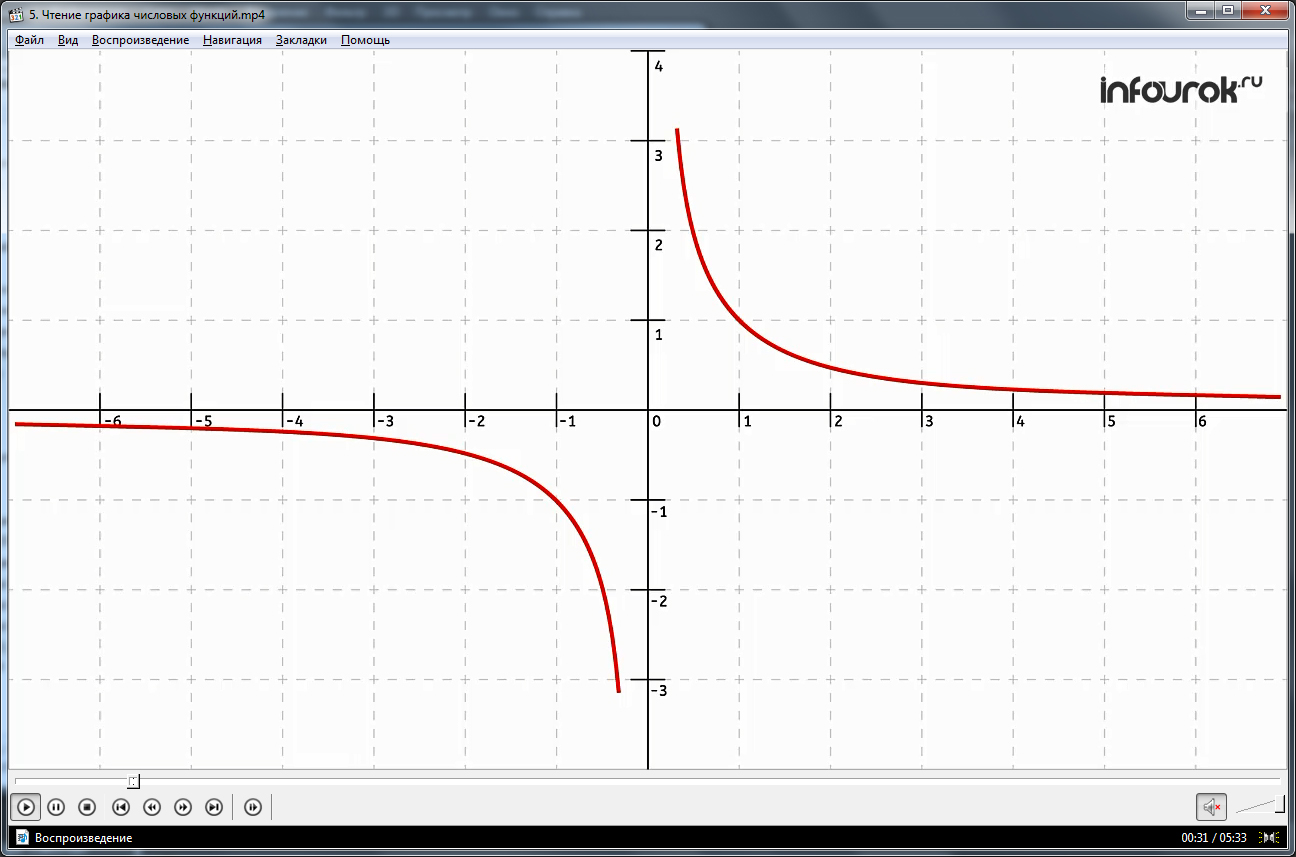
Автор урока обращает внимание слушателей на то, что чтение графиков числовых функций имеет широкое применение в нашей жизни. Особенно часто чтение графиков используется в экономике. При этом на экране изображен график некоторой функции.

Здесь же автор предлагает вспомнить, какая функция называется числовой. Пока обучающиеся начинают вспоминать, он напоминает им данное понятие. При этом объяснение сопровождается иллюстрацией. При этом, получается, что необходимо также вспомнить, что называется областью определения и областью значений функции. Автор напоминает и то, как выглядит уравнение функции в общем виде.

Чтобы обучающимся было проще понять принцип чтения графиков функций, необходимо вспомнить, что называется аргументом, то есть зависимой переменной, и независимой переменной. После этого предлагается рассмотреть некоторую произвольную функцию и построить ее график, подобрав пары чисел, которые являются координатами точек в системе координат. Когда график построен, вводится определение графика функции.

Далее автор говорит, что означает прочитать график функции. Получается, что для этого необходимо перечислить ее свойства, которые видны по графику. При этом перечисляются те свойства, которыми обладают все функции, и те, которыми обладают только некоторые функции.

Затем предлагается рассмотреть в качестве примеров, известные функции, которые были изучены в курсе алгебры ранее. Таких функций рассматривается две, последовательно. Сначала на экране изображается график функции, а затем подробно описывается каждое свойство, которым обладает функция. На каждом пункте автор останавливается и поясняет, что и как получается.

На этом видеоурок завершается, но не заканчивается занятие в школе. Поэтому оставшееся время желательно посвятить закреплению материала, подобрав для этого необходимые задания.

Урок будет полезен как для учителей, так и для обучающихся.

Чтение графика числовой функции.

Чтение графиков функций имеет большое практическое значение. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.

Для изучения сегодняшней темы нам необходимо вспомнить: какая функция называется числовой?

Числовой функцией называется правило, с помощью которого каждому элементу из множества икс большое мы ставим в соответствие единственный элемент из множества игрек большое.

Множество Х называется областью определения функции.

Множество У называется множеством значений функции.

Равенство игрек равен эф от икс называется уравнением функции.

А что называется графиком функции?

Если дана функция игрек равно эф от х, где икс принадлежит икс большому и возьмем все пары икс, игрек и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами икс большое и игрек большое.

1)область определения функции;

2)область значений функции;

3)нули функции – значения аргумента, при которых функция равна нулю;

4)промежутки знакопостоянства функции, т.е.промежутки,

где значения функции имеют один и тот же знак;

5)промежутки монотонности функции, т.е. промежутки, где функция возрастает или убывает;

6)наибольшееи наименьшее значения функции, т.е. самое большое и самое маленькое значение зависимого переменного;

Свойства, которые имеют не все функции:

9) четность, нечетность;

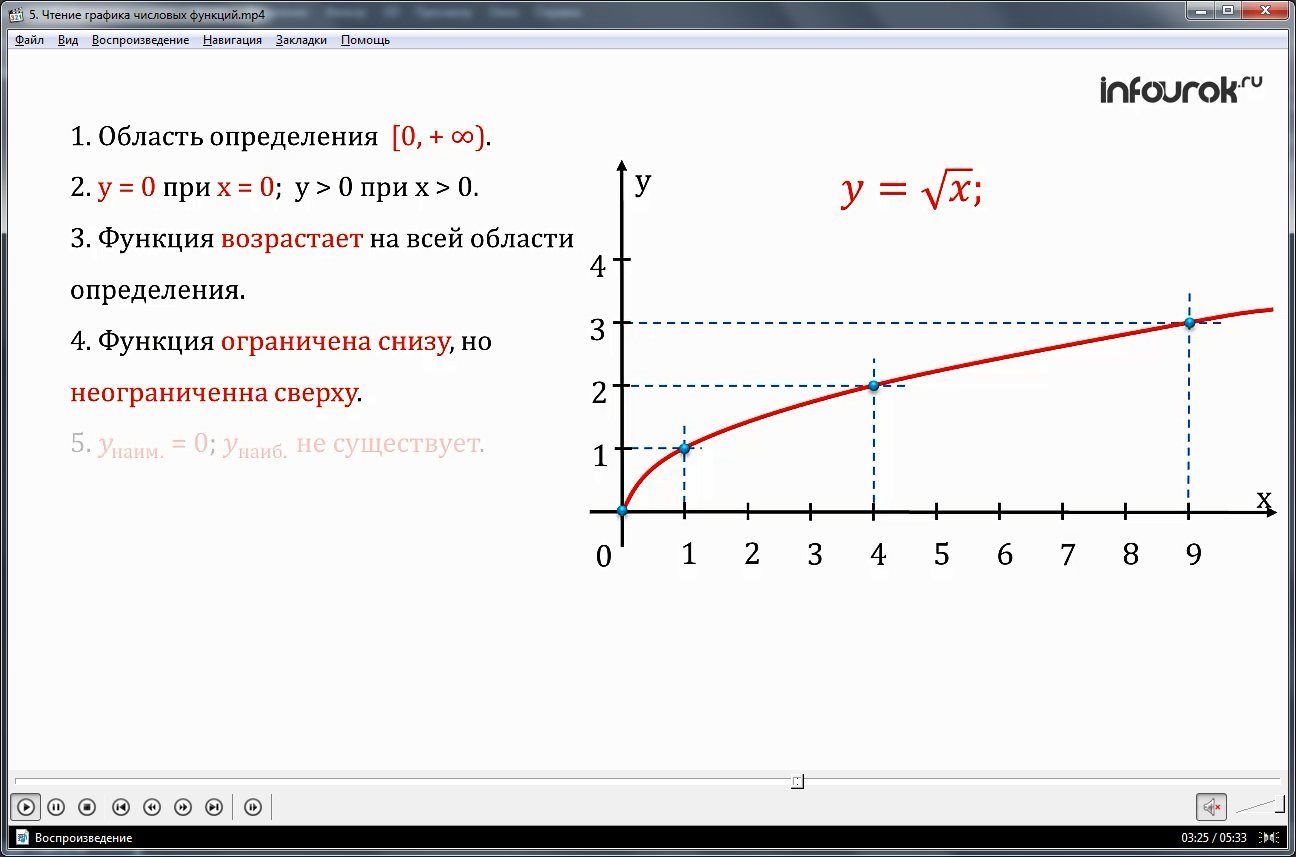
Прочитаем графики известных нам функций, например,игрек равен квадратный корень из икс.

1. Область определения функции —

луч от нуля до плюс бесконечности
2. Игрек равен нулю при икс равному нулю; игрек больше нуля при икс больше нуля.

3. Функция возрастает на всей области определения.

6.Функция непрерывна в заданной области определения.
7. Область значений функции — луч от нуля до плюс бесконечности
8.График обращен выпуклостью вверх.
у=кх+в

Прочитаем график ограниченной функции, график которой изображен

1.Область определения функции – отрезок от минус трех до трех.

7.Функция ограничена и сверху и снизу.

8.На отрезке минус трех до нуля функция выпукла вниз, а

на отрезке нуля до трех выпукла вверх.

9.Непрерывна на всей области определения.

Сегодня, мы научились читать графики элементарных функций. На следующем уроке мы продолжим чтение графиков тригонометрических функций, показательной, логарифмической.

Источник

Построение графиков функций

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Сдвигаем график вправо на 1:

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Источник

Чтение графиков и диаграмм

Урок 7. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Чтение графиков и диаграмм»

Напомним, что график – это чертёж, который применяют для наглядного изображения зависимости какой-либо одной величины от другой. Другими словами, график – это линия, которая даёт наглядное представление о характере изменения функции или о каких-либо табличных данных.

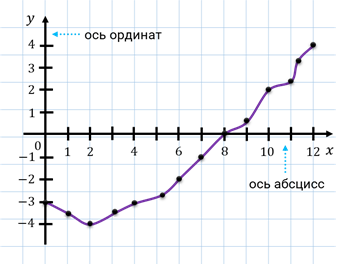
Как правило, график располагают на координатной плоскости, в которой горизонтальная ось называется осью абсцисс, вертикальная ось – осью ординат.

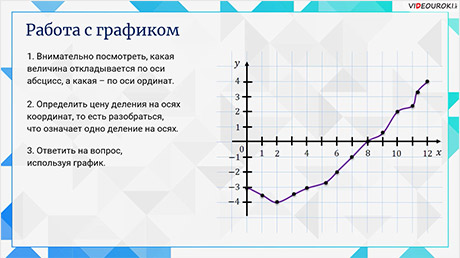
Для работы с графиками главное:

1. Внимательно посмотреть, какая величина откладывается по оси абсцисс, а какая – по оси ординат.

2. Определить цену деления на осях координат, то есть разобраться, что означает одно деление на осях.

3. Ответить на вопрос, используя график.

Также напомним, что диаграмма — графическое представление данных, позволяющее быстро оценить соотношение нескольких величин.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

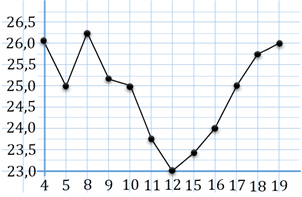
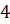
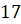
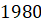
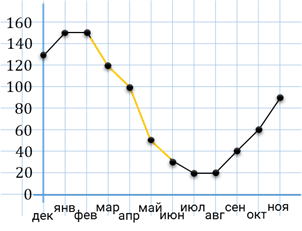
Задание первое. На рисунке жирными точками показана среднесуточная температура воздуха в Риге за каждый день с по апреля года. По горизонтали указаны числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какого числа среднесуточная температура была наименьшей за данный период.

Решение. Так как в вопросе задачи нас просят определить, какого числа среднесуточная температура была наименьшей за данный период, то на графике нам необходимо найти точку, где значение по оси ординат будет наименьшим, то есть найти такую точку, которая будет расположена ниже всех остальных. Нужная нам точка имеет координаты 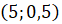. Числа месяца отмечены на горизонтальной оси. Следовательно, пятого числа среднесуточная температура была наименьшей за данный период.

В ответе запишем 5.

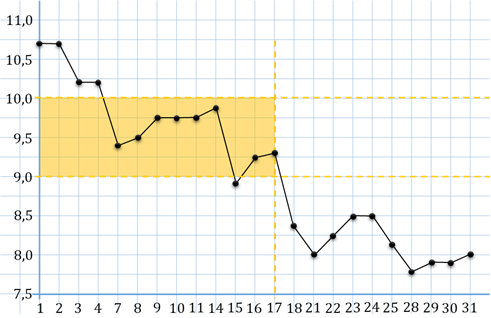
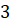
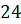
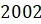
Задание второе. На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с по октября года. По горизонтали указываются числа месяца, по вертикали — цена золота в долларах США за унцию. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую цену золота на момент закрытия торгов за данный период. Ответ дайте в долларах США за унцию.

Решение. Цена золота отмечена на вертикальной оси, а числа месяца – на горизонтальной. Так как в вопросе задачи нас просят определить наименьшую цену золота, то на графике нам необходимо найти точку, значение которой по оси ординат будет наименьшим, то есть найти такую точку, которая будет расположена ниже всех остальных. Видим, что нужная точка расположена в промежутке между числами 312 и 310.

,

.

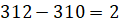
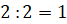
То есть цена деления одной клеточки равна 1 доллару США за унцию. Тогда понятно, что искомая цена золота составляет 311 долларов США за унцию.

В ответе запишем 311.

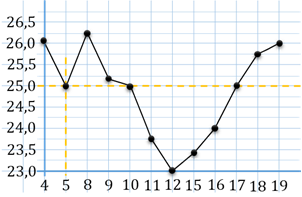
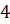
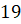
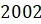
Задание третье. На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с по апреля года. По горизонтали указываются числа месяца, по вертикали – цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линиями. Определите по рисунку, какого числа цена нефти на момент закрытия торгов впервые за данный период составила 25 долларов за баррель.

Решение. Чтобы ответить на вопрос задачи, нам нужно на вертикальной оси найти число 25, то есть 25 долларов за баррель. Мы смотрим на график и прокладываем горизонтальную черту на уровне 25. Обратите внимание, нашим ответом будет первая точка, которая будет на проведённой нами прямой, то есть самая левая. Итак, находим эту точку. Затем проводим вертикальную прямую до пересечения с осью абсцисс. И видим, что 5-го числа цена нефти на момент закрытия торгов впервые за данный период составила 25 долларов за баррель.

В ответе запишем 5.

Задание четвёртое. На рисунке жирными точками показана цена серебра, установленная Центробанком Российской Федерации, во все рабочие дни в октябре года. По горизонтали указываются числа месяца, по вертикали – цена серебра в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода цена серебра была между и рублями за грамм.

Решение. Чтобы ответить на вопрос задачи, нам нужно найти все те дни, которые будут относиться к промежутку между и рублями за грамм. Для этого на вертикальной оси мы найдём числа 9 и 10, то есть 9 и 10 рублей за грамм. Затем проведём горизонтальные линии на уровне этих чисел. Обратите внимание, последний день, когда цена серебра за грамм была между и рублями – это 17 число. Также следует отметить, что за этот период цена серебра за грамм 15 числа была меньше 9 рублей. Значит, этот день нам нужно будет исключить. Итак, теперь посчитаем, сколько же рабочих дней из данного периода цена серебра была между девятью и десятью рублями за грамм. В результате получим 8 рабочих дней.

В ответе запишем 8.

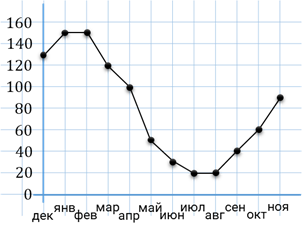
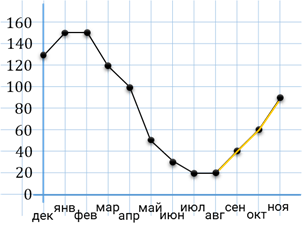
Задание пятое. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали – количество проданных обогревателей. Для наглядности точки соединены линией. Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.

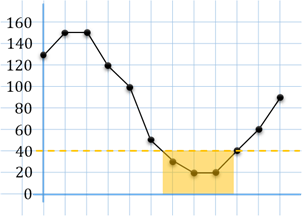
Решение. Итак, прочитаем первую характеристику. Нам нужно найти период, когда ежемесячный объём продаж был меньше 40 штук в течение всего периода. Количество проданных обогревателей отмечено на вертикальной оси. Тогда найдём на вертикальной оси число 40 и проведём горизонтальную линию на уровне этого числа. По графику видно, что период, когда ежемесячный объём продаж был меньше 40 штук, приходился на лето.

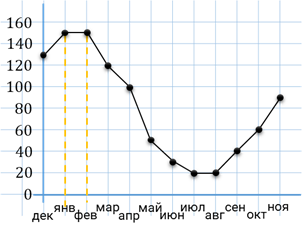
Перейдём ко второй характеристике. Здесь нам нужно найти период, когда ежемесячный объём продаж достиг максимума. Для этого на графике нам необходимо найти точку, значение которой по оси ординат будет наибольшим, то есть найти такую точку, которая будет расположена выше всех остальных. Видим, на графике есть две такие точки. Проведём из этих точек вертикальные линии до пересечения с осью абсцисс. Теперь понятно, что в январе и феврале ежемесячный объём продаж достиг максимума. А эти два месяца относятся к зиме.

Следующая характеристика: ежемесячный объём продаж падал в течение всего периода. На горизонтальной оси указаны месяцы. Рассмотрим внимательно график и найдём такой промежуток, в котором график постоянно идёт вниз. Несложно заметить, что график постоянно идёт вниз в марте, апреле и мае. А эти месяцы относятся к весне.

И последняя характеристика: ежемесячный объём продаж рос в течение всего периода. В этом случае нам нужно найти такой промежуток графика, в котором график постоянно идёт вверх. Внимательно посмотрев на график, видно, что в сентябре, октябре и ноябре график постоянно идёт вверх. А эти месяцы относятся к осени.

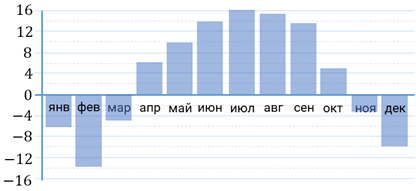
Задание шестое. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 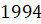года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в году. Ответ дайте в градусах Цельсия.

Решение. Температура откладывается по оси ординат. Поэтому нам нужна самая высшая точка на диаграмме. Мы видим, что самый длинный столбик, направленный вверх, находится на уровне седьмого месяца. Понятно, что искомая среднемесячная температура составляет .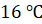

В ответе запишем .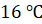

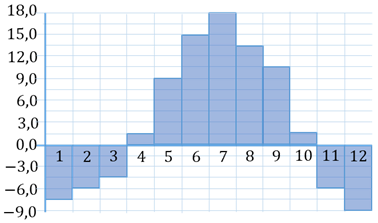
Задание седьмое. Среднемесячная температура воздуха в Ижевске за каждый месяц года показана на диаграмме. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме среднюю температуру летом года.

Решение. На горизонтальной оси отмечены месяцы. Напомним, что к летним месяцам относятся шестой, седьмой и восьмой месяцы. На вертикальной оси указана температура. Тогда столбику, расположенному в шестом месяце, соответствует температура , столбику, расположенному в седьмом месяце, – 1. А вот значение градусов, соответствующее столбику, расположенному в восьмом месяце, находится между и . Получается, что разность между этими двумя числами равна трём. Эти 3 градуса нужно разбить на 2 деления. Поэтому понятно, что в одном делении откладывается , так как . Тогда столбику, расположенному в восьмом месяце, соответствует температура ().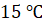

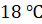
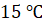
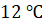
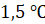
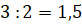
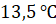
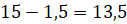
Тогда средняя температура за летние месяцы:

.

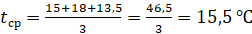
В ответе запишем .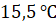

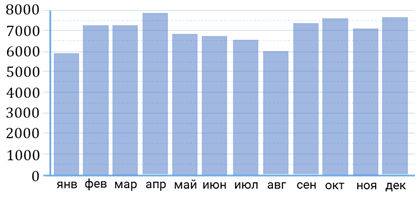
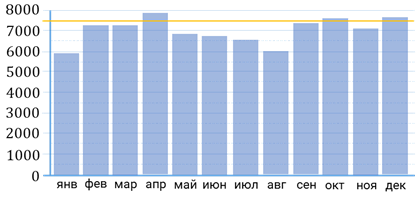
Задание восьмое. На диаграмме показано среднесуточное количество перевезённых пассажиров в Московском метрополитене за каждый месяц 2008 года (в тысячах человек). Сколько было месяцев, в каждый из которых среднесуточное число перевезённых пассажиров составило не менее 7500 человек?

Решение. На вертикальной оси отмечено количество пассажиров, перевезённых в Московском метрополитене. Найдём на вертикальной оси значение 7500. Для этого нам нужно определить цену деления. Так как второму делению на вертикальной оси соответствует отметка в 1000 человек, то цена одного деления будет равна 500. Тогда значение 7500 на вертикальной оси будет расположено посередине между числами 7000 и 8000. Проведём горизонтальную прямую на уровне 7500. И посчитаем, сколько столбиков будут расположены выше нашей линии. Итак, видим, что у нас таких столбиков 3.

В ответе запишем 3.

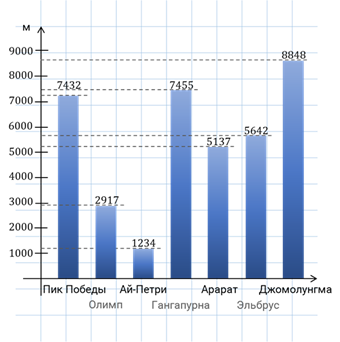
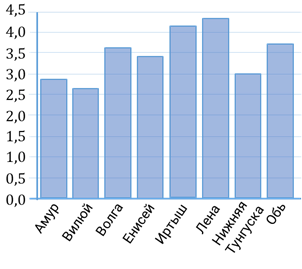
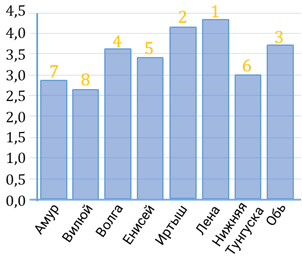
Задание девятое. На диаграмме приведены данные о длине восьми крупнейших рек России (в тысячах километров). Первое место по длине занимает река Лена. На каком месте по длине находится река Амур?

Решение. Для начала расположим названия рек в порядке убывания их длин. Для того чтобы делать это задание не на глаз, давайте приложим линейку к самому высокому столбику и затем будем медленно опускаться вниз, записывая реки в порядке убывания их длин. Итак, первое место – Лена, второе – Иртыш, третье место – Обь, четвёртое – Волга, пятое место – Енисей, шестое – Нижняя Тунгуска, седьмое место – Амур и восьмое – Вилюй. Амур находится на седьмом месте.

В ответе запишем 7.

В завершение урока хочется сказать, что задания на тему чтение графиков и диаграмм не такие уж и сложные. Чтобы не было ошибок, главное:

1. Внимательно прочитать условие задачи.

2. Определить, относительно какой оси нужно искать искомую величину.

3. Разобраться с ценой деления на осях координат.

Источник