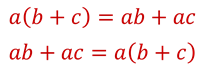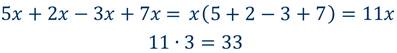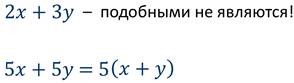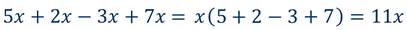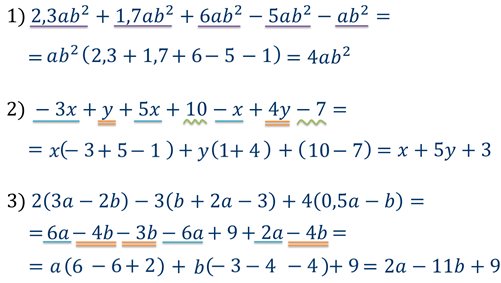Что значит привести подобные слагаемые 6 класс

Подобные слагаемые, их приведение, примеры

Приведение подобных слагаемых является одним из наиболее употребимых тождественных преобразований. В этом разделе мы дадим определение термина, разберем, что обозначает словосочетание «приведение подобных слагаемых», рассмотрим основные правила выполнения действий и наиболее распространенные типы задач.

Определение и примеры подобных слагаемых

В большинстве учебных пособий тема подобных слагаемых разбирается после знакомства с буквенными выражениями, когда появляется необходимость проводить с ними различные преобразования.

Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.

Слагаемые – это, как известно, составные элементы суммы. Это значит, что они могут присутствовать лишь в тех выражениях, которые представляют собой сумму. Буквенная часть – это одна или произведение нескольких букв, которые представляют собой переменные. Слагаемые с буквенной частью – это произведение некоторого числа и буквенной части. Здесь некоторое число также носит название числового коэффициента.

Буквенная часть может быть представлена не только произведением букв, но также и произвольным буквенным выражением. Например:

Обобщим изложенные выше утверждения и дадим еще одно определение подобных слагаемых.

Подобные слагаемые – это слагаемые в буквенном выражении, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части, если под буквенной частью понимать любое буквенное выражение.

Числовые коэффициенты подобных слагаемых могут быть равны, тогда мы говорим о том, что подобные слагаемые одинаковые. Если же числовые коэффициенты различаются, то подобные слагаемые будут разными.

Возьмем для примера выражение 2 · x · y + 3 · y · x и рассмотрим такой нюанс: являются ли слагаемые 2 · x · y и 3 · y · x подобными. В задачах этот вопрос может иметь следующую формулировку: одинаково ли буквенное выражение части x · y и y · x указанных слагаемых? Буквенные множители в приведенном примере имеют различный порядок, что в свете данного выше определения не делает их подобными.

К слову, в некоторых источниках при нестрогом отношении к вопросу, слагаемые из примера могут называться подобными. Но лучше не допускать таких неточностей в трактовках.

Приведение подобных слагаемых, правило, примеры

Под преобразованием выражений, которые содержат подобные слагаемые, подразумевается проведение сложения этих слагаемых. Проводится это действие обычно в три этапа:

Приведем пример таких вычислений.

Описанные три шага для экономии времени записывают в виде правила приведения подобных слагаемых. Согласно правило для того, чтобы привести подобные слагаемые, необходимо сложить их коэффициенты, а затем умножить полученный результат на буквенную часть при ее наличии.

Решение

Источник

Подобные слагаемые

Урок 42. Математика 6 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Подобные слагаемые»

Сегодня на уроке мы узнаем, какие слагаемые называют подобными, а также научимся приводить подобные слагаемые или, проще говоря, упрощать выражения.

Для изучения нового материала нам понадобятся понятие «коэффициента» и знание распределительного свойства умножения. Вспомним их.

Коэффициентом называют числовой множитель, который записан перед буквенным (одним или несколькими) множителем.

Распределительное свойство умножения справедливо для любых чисел a, b и c.

Оно позволяет, как раскрывать скобки, так и выносить общий множитель за скобки.

Часто при работе с выражениями сначала их обычно упрощают, т.е. преобразуют в более компактную и удобную для вычислений форму.

Найти значение выражения 5х + 2х – 3х + 7х при х = 3.

Конечно, можно просто подставить вместо х указанное значение и посчитать сумму полученных произведений.

Но такой процесс вычислений займёт немало времени. Вычисления значительно упростятся, если обратить внимание, на то, что все слагаемые имеют один и тот же буквенный множитель х. И вот тут к нам на помощь приходит распределительное свойство умножения. Мы знаем, что на основании распределительного свойства можно выносить общий множитель за скобки. Вынесем в нашем выражении общий буквенный множитель х за скобки.

Смотрите, как мы себе упростили вычисления. Такие преобразования можно выполнять только в тех случаях, когда слагаемые имеют одинаковую буквенную часть.

Такие слагаемые называют подобными, а сами преобразования называют приведением подобных слагаемых.

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Замену суммы подобных слагаемых одним слагаемым называют приведением подобных слагаемых.

Подобные слагаемые могут отличаться только коэффициентами. Кроме того, подобными считают и равные слагаемые, а также числа.

Заметим, что слагаемые, у которых равны коэффициенты, а буквенные множители различны, подобными не являются, хотя и к ним иногда полезно применять распределительное свойство умножения.

Ответим на вопрос: зачем же нужно приводить подобные слагаемые?

Ответ на этот вопрос прост. Приводят подобные слагаемые для того, чтобы сделать суммы более короткими, т.е. преобразовывают их в суммы с меньшим числом слагаемых.

Посмотрите, в нашей начальной сумме было 4 слагаемых, а мы её преобразовали в выражение, состоящее из двух множителей. С более короткими суммами легче выполнять вычисления.

Запишем правило, по которому приводят подобные слагаемые:

Для того чтобы привести подобные слагаемые, надо:

1) сложить коэффициенты подобных слагаемых;

2) результат умножить на общую буквенную часть.

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Замену суммы подобных слагаемых одним слагаемым называют приведением подобных слагаемых.

Для того чтобы привести подобные слагаемые, надо:

1) сложить коэффициенты подобных слагаемых;

2) результат умножить на общую буквенную часть.

Источник

Подобные слагаемые, их приведение, примеры.

Одним из наиболее часто используемых тождественных преобразований является приведение подобных слагаемых. В этой статье мы дадим определение подобных слагаемых, разберемся, что называют приведением подобных слагаемых, рассмотрим правила, по которым выполняется это действие, и приведем примеры приведения подобных слагаемых с подробным описанием решения.

Навигация по странице.

Определение и примеры подобных слагаемых.

Разговор о подобных слагаемых возникает после знакомства с буквенными выражениями, когда возникает необходимость проведения преобразований с ними. По учебникам математики Н. Я. Виленкина определение подобных слагаемых дается в 6 классе, и оно имеет следующую формулировку:

Подобные слагаемые – это слагаемые, которые имеют одинаковую буквенную часть.

Стоит внимательно разобраться в этом определении. Во-первых, речь идет о слагаемых, а, как известно, слагаемые являются составными элементами сумм. Значит, подобные слагаемые могут присутствовать лишь в выражениях, которые представляют собой суммы. Во-вторых, в озвученном определении подобных слагаемых присутствует незнакомое понятие «буквенная часть». Что же понимают под буквенной частью? Когда дается это определение в шестом классе, под буквенной частью понимается одна буква (переменная) или произведение нескольких букв. В-третьих, остается вопрос: «А что же это за такие слагаемые с буквенной частью»? Это слагаемые, представляющие собой произведение некоторого числа, так называемого числового коэффициента, и буквенной части.

Дальше из контекста указанного выше учебника становится видно дополнение к определению подобных слагаемых – слагаемые в буквенном выражении, не имеющие буквенной части, также называют подобными.

Позже расширяется и понятие буквенной части – буквенной частью начинаю считать не только произведение букв, а произвольное буквенное выражение. К примеру, в учебнике алгебры для 8 класса авторов Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова под редакцией С. А. Теляковского приведена сумма вида , и сказано, что составляющие ее слагаемые являются подобными. Общей буквенной частью этих подобных слагаемых является выражение с корнем вида .

Обобщив всю изложенную информацию, можно дать следующее определение подобных слагаемых.

Подобными слагаемыми называются слагаемые в буквенном выражении, имеющие одинаковую буквенную часть, а также слагаемые, не имеющие буквенной части, где под буквенной частью понимается любое буквенное выражение.

Отдельно скажем, что подобные слагаемые могут быть одинаковыми (когда равны их числовые коэффициенты), а могут быть и разными (когда их числовые коэффициенты различны).

Приведение подобных слагаемых, правило, примеры

Приведение подобных слагаемых проводится в три этапа:

Для удобства три перечисленных выше шага объединяют в правило приведения подобных слагаемых: чтобы привести подобные слагаемые, нужно сложить их коэффициенты и полученный результат умножить на буквенную часть (если она есть).

Для закрепления материала рассмотрим решение еще одного примера.

Источник

41. Подобные слагаемые

Замену выражения (а + b) • с выражением ас + bс или выражения с • (а + b) выражением са + сb также называют раскрытием скобок.

Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.

Подобные слагаемые могут отличаться только коэффициентами.

Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Вопросы для самопроверки

Выполните упражнения

1281. Раскройте скобки:

1282. Выполните действия, применив распределительное свойство умножения:

1283. Сложите подобные слагаемые:

— сумма семи икс, минус трёх икс, шести икс и минус четырёх икс,

— семь икс минус три икс плюс шесть икс минус четыре икс.

1284. Выполните приведение подобных слагаемых:

1285. Раскройте скобки и приведите подобные слагаемые:

1286. Найдите значение выражения:

1288. В мешок помещается 20 кг картофеля или 14 кг капусты. В столовую привезли картофеля на 3 мешка больше, чем капусты. Всего привезли 1,62 ц картофеля и капусты. Сколько привезли мешков картофеля и сколько капусты?

1289. Турист шёл 3 ч пешком и 4 ч ехал на велосипеде. Всего он проделал путь в 62 км. С какой скоростью турист шёл пешком, если он шёл на 5 км/ч медленнее, чем ехал на велосипеде?

1290. Вычислите устно:

1292. Найдите значение выражения:

1294. Выполните умножение:

1295. Чему равен коэффициент в каждом из выражений:

1296. Расстояние от Москвы до Нижнего Новгорода 440 км. Каким должен быть масштаб карты, чтобы на ней это расстояние имело длину 8,8 см?

1297. Отрезком какой длины изображается на карте расстояние 35 км, если масштаб карты 1 : 100 000?

1298. Расстояние от Киева до Одессы изображается на карте, масштаб которой 1 : 10 000 000, отрезком 6,5 см. Определите это расстояние на местности.

1299. Прямоугольник на плане, масштаб которого 2 : 5, имеет длину 38 мм, а ширину 26 мм. Найдите площадь этого прямоугольника в натуре.

1300. Отрезок на плане, масштаб которого 2 : 7, изображается отрезком 4,2 см. Какой длины будет этот отрезок на плане, сделанном в масштабе 5 : 3?

Кто на каком инструменте играет и какой иностранный язык знает?»

1305. Найдите значение выражения, применив распределительное свойство умножения:

1306. Приведите подобные слагаемые:

1307. Раскройте скобки и приведите подобные слагаемые:

1308. Решите уравнение:

1309. Группа туристов 1 ч ехала на автобусе, а затем 6 ч шла пешком со скоростью на 18 км/ч меньшей, чем скорость автобуса. Всего группа преодолела 67 км. Найдите скорость автобуса и туристов в пешем походе.

1310. В трёх классах 71 учащийся. В первом классе учащихся на 4 человека больше, чем во втором, и на 3 человека меньше, чем в третьем классе. Сколько учащихся в каждом классе?

1311. Определите масштаб карты, если расстояние между двумя пунктами на местности 750 м, а на карте 25 мм.

1312. Какой длины отрезком изображается на карте расстояние 6,5 км, если масштаб карты 1 : 25 000?

1313. На карте отрезок имеет длину 12,6 см. Какова длина этого отрезка на местности, если масштаб карты 1 : 150 000?

Источник

Конспект урока по теме «Подобные слагаемые»

Открытие способа приведения подобных слагаемых

Планируемые образовательные результаты

Содержимое разработки

Автор: учитель Смехова Ирина Геннадьевна, МАОУ «Средняя общеобразовательная школа №1» г. Набережные Челны.

Тема урока: Приведение подобных слагаемых.

Тип урока: урок изучения нового материала.

Вид урока: формирование УДД.

Цели урока: Открытие способа приведения подобных слагаемых

1) формирование понятия «подобные слагаемые» и умения приводить подобные слагаемые.

2) развивать критическое мышление, умение анализировать, сравнивать;

3) способствовать формированию: навыков самостоятельной работы; умению аккуратно и грамотно выполнять математические записи, способствовать воспитанию организованности.

Планируемые результаты изучения темы:

Предметные:
Знание правила приведения подобных слагаемых.
Умение находить в выражениях подобные слагаемые и приводить их.

Владение в практике правилом приведения подобных слагаемых, употребление в речи математической терминологии, выполнять задания творческого и поискового характера.

Формы организации познавательной деятельности: фронтальная, индивидуальная, работа в парах.
Оборудование урока: мультимедийная презентация, учебник, карточки контроля, памятка составления синквейна.
Основные понятия: Подобные слагаемые, приведение подобных слагаемых.

Структура и ход урока

Актуализация ранее изученного материала.

-Расскажите правило раскрытия скобок

3(5+х)= (какое свойство вы применяли? (распределительное свойство умножения))

Б) Упростить выражения

(дать определение коэффициенту)

В) Упростить выражения

13 b + b = с помощью какого свойства вы будете упрощать? (распределительное свойство умножения)

– n – 18 n +5 = здесь можно выполнить упрощение выражения? Попробуйте выполнить.

Постановка проблемной задачи

Упростите еще одно выражение:

С такими вы еще не встречались? Попробуйте упростить выражение. Работаем в парах.У вас на столе есть листочки. Обсудите в паре и выполните задание. Рассмотрим ваши решения. (ученики выходят к доске и записывают свои варианты решения.) Теперь давайте проверим. (ответ на слайде). Расскажите, как вы выполнили это задание? (выслушать варианты ответов, выявить признаки подобия)

И тема нашего урока ПРИВЕДЕНИЕ ПОДОБНЫХ СЛАГАЕМЫХ. Запишите в тетради.

Назовите цели урока

(узнать какие слагаемые называются подобными и как их приводить)

Постановка учебной задачи

Ребята кто-то уже может дать определение подобным слагаемым? Обсудите в парах. Выслушать варианты и проверить на слайде. Если возникли затруднения объяснить на примерах. Выводы.

Слагаемые имеющие одинаковую буквенную часть называются подобными.

Подобные слагаемые могут отличаться только коэффициентами
(запишите в тетради)

Что такое подобные слагаемые мы выяснили. А что значит приведение, вы уже догадались? (выслушать варианты ответов)

Вывод: Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.

Посмотрите на пример. Что можно сделать чтобы легче было привести подобные слагаемые. (выделить их). Как бы вы это сделали? После предложений дать пояснение, как это принято в математике. Да, для удобства нужно подчеркнуть подобные слагаемые.

4х+7у-16+17-6х-3у (записывают в тетради, решают, проверяем на слайде)

VI . Закрепление и совершенствование знаний, умений и навыков.

Для закрепления выполняют задания из учебника

№ 1283 (а,г), № 1284 (а,б) (после каждого задания проверка)

У каждого учащегося своя карточка с критериями оценивания.

в) – 15 x + 10 y + 12 x – 1 =

а) 23 x – 23 + 40 + 4 x =

б) y + 124 + a – 124 – y =

в) 9 a + 13 b – 5 + 8 a =

Предлагаю вам самостоятельную работу оценить по критериям. Из предложенных критериев выберете те, по которым вы будете оценивать работу соседа. Может тут есть лишние? (на доске записать номера критериев) На столе так же лежат листочки со списком критериев. (лишнее пункт 6, почему? Нет примеров со скобками)

Все задания выполнены верно

Подчеркнуты все подобные слагаемые

Приведены все подобные слагаемые

Нет вычислительных ошибок.

В ответе не «потерян» знак минус

Правильно раскрыты скобки

Самостоятельную работу проверяют в парах по слайду (меняются тетрадями) Опрос по результатам. Скажите какие возникли затруднения?

Выставляют оценку с учетом количества «+» по выбранным критериям. Опрос оценок в классе.

Ваша задача творчески обсудить тему нашего урока и составить синквейн на тему «Подобные слагаемые». Правило составления синквейна на экране. Работаем в парах. Выслушать предложение и сообща составить и записать синквейн.

Источник