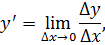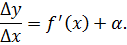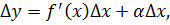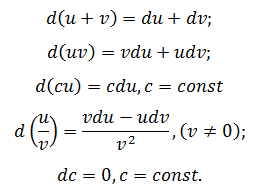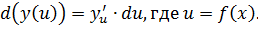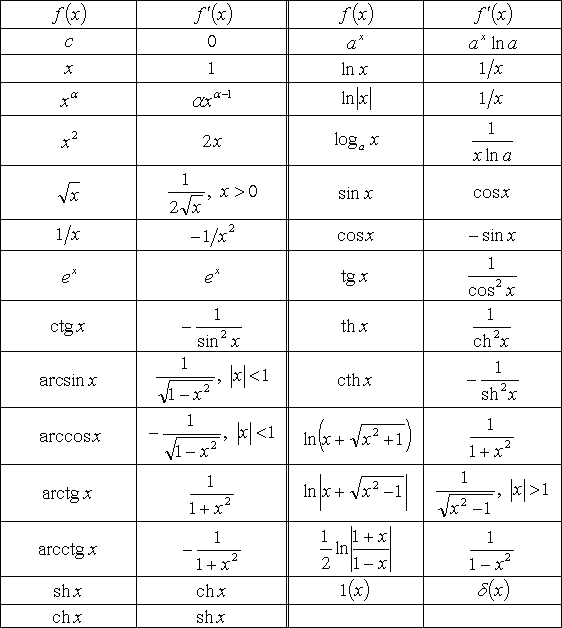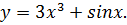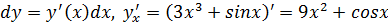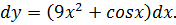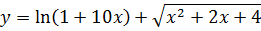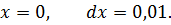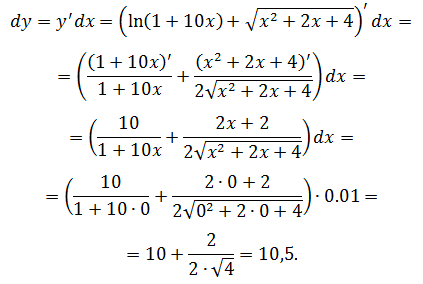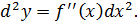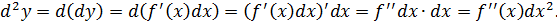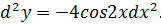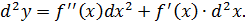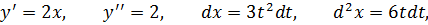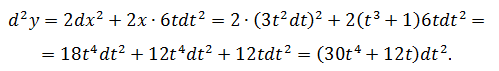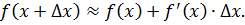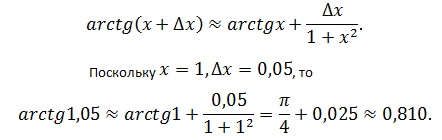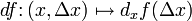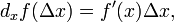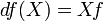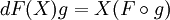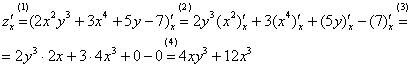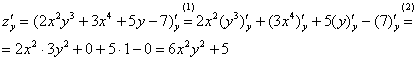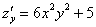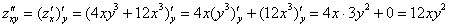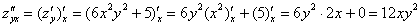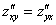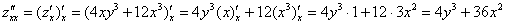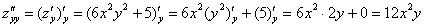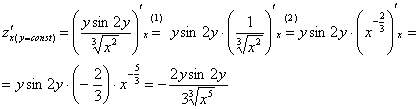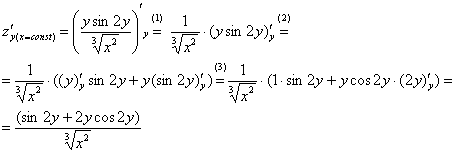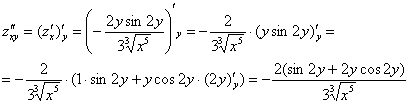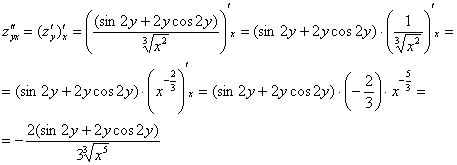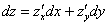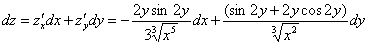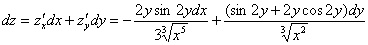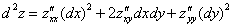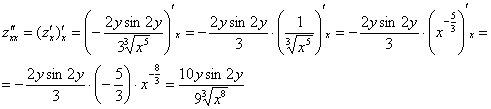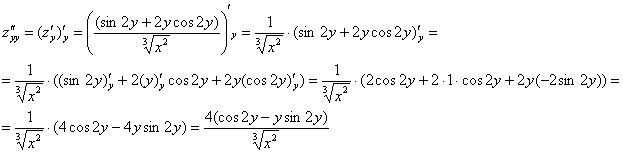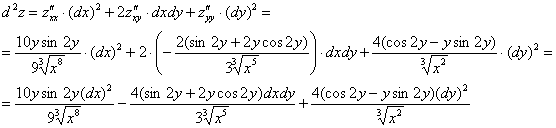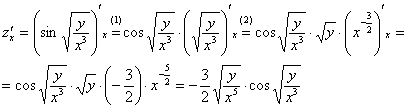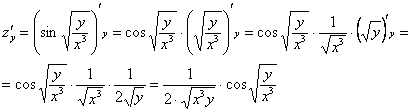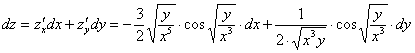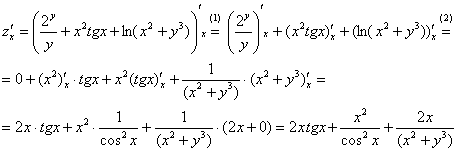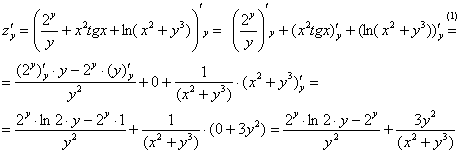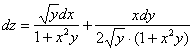Что значит полный дифференциал

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

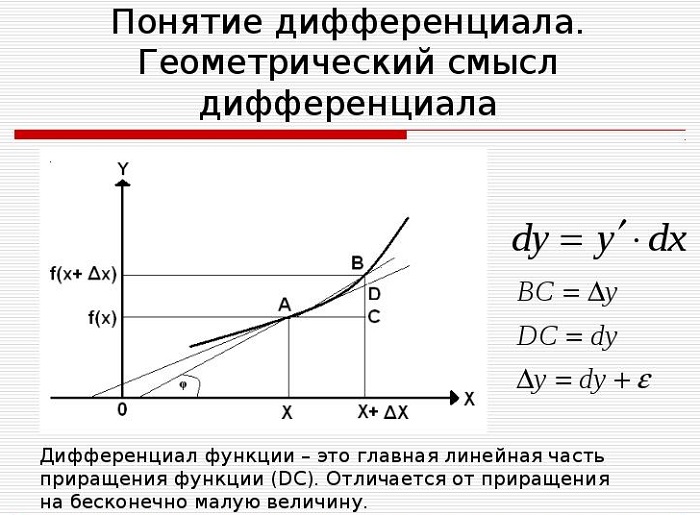
Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

Полный дифференциал

Дифференциа́л в математике — линейная часть приращения функции или отображения. Это понятие тесно связанное с понятием производной по направлению.

Содержание

Неформальное описание

в частности, разность приращения функции и её дифференциала — бесконечно малая величина:

Определения

Для функций

Дифференциал гладкой вещественнозначной функции f определённой на M ( M — область в или гладкое многообразие) представляет собой 1-форму и обычно обозначается df и определяется соотношением

Для отображений

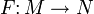
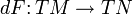
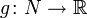
Дифференциал гладкого отображения из гладкого многообразия в многообразие есть отображение между их касательными расслоениями, , такое что для любой гладкой функции имеем

Это понятие естественно обобщает дифференциал функции.

Связанные определения

Свойства

Примеры

История

Термин Дифференциал (от лат. differentia — разность, различие) введён Лейбницем. Изначально, dx применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики (за исключением нестандартного анализа).

См. также

Полезное

Смотреть что такое «Полный дифференциал» в других словарях:

полный дифференциал — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN ordinary differentialtotal differential … Справочник технического переводчика

Полный дифференциал — функции f (x, у, z. ) нескольких независимых переменных выражение в случае, когда оно отличается от полного приращения (См. Полное приращение) Δf = f (x + Δx, y + Δy, z + Δz,…) f (x, y, z, …) на… … Большая советская энциклопедия

ДИФФЕРЕНЦИАЛ — (лат., от differe различать). Предел бесконечно малой разности между функцией переменного, получившего бесконечно малое приращение, и первоначальной функцией того же переменного (мат. терм.). Словарь иностранных слов, вошедших в состав русского… … Словарь иностранных слов русского языка

Дифференциал (механика) — У этого термина существуют и другие значения, см. Дифференциал (значения). Устройство дифференциала (центральная часть) Дифференциал это механическое устройство, котор … Википедия

Дифференциал (автомобиль) — Устройство дифференциала(центральная часть) Дифференциал это механическое устройство, которое передает вращение с одного источника на два независимых потребителя таким образом, что угловые скорости вращения источника и обоих потребителей могут… … Википедия

Полный привод — У этого термина существуют и другие значения, см. Полный привод (значения). Наиболее распространённая (но не единственная) схема трансмиссии полноприводного автомобиля. Полный привод (4×4, 4WD … Википедия

Постоянный полный привод — Наиболее распространённая (но не единственная) схема трансмиссии полноприводного автомобиля. Полный привод (4×4, 4WD, AWD) конструкция трансмиссии автомобиля, когда крутящий момент, создаваемый двигателем, передаётся на все колеса. До… … Википедия

Теплота — 1) Т. мы называем причину, вызывающую в нас специфические, всем известные тепловые ощущения. Источником этих ощущений являются всегда какие либо тела внешнего мира, и, объективируя наши впечатления, мы приписываем этим телам содержание некоторого … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Источник

Дифференциал функции определение, виды, свойства, формула полного дифференциала функции, геометрический смысл, правило применения, примеры решения уравнений

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.

Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

Что такое дифференциал функции?

Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений.

Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента.

История открытия дифференциала

Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света.

Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления.

Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени.

Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке.

В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни.

Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач.

Геометрический смысл дифференциала

Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx.

Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть.

Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений.

Применение дифференциала в приближенных вычислениях

Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений.

С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности.

Использование дифференциала для оценки погрешностей

Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов.

Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью».

Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью».

Для оценки величины погрешностей измерений используют дифференциальное исчисление.

Источник

Частные производные функции двух переменных.
Понятие и примеры решений

На данном уроке мы продолжим знакомство с функцией двух переменных и рассмотрим, пожалуй, самое распространенное тематическое задание – нахождение частных производных первого и второго порядка, а также полного дифференциала функции. Студенты-заочники, как правило, сталкиваются с частными производными на 1 курсе во 2 семестре. Причем, по моим наблюдениям, задание на нахождение частных производных практически всегда встречается на экзамене.

Для эффективного изучения нижеизложенного материала вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде. Раздобыть справочный материал можно на странице Математические формулы и таблицы.

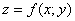
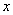
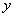
Быстренько повторим понятие функции двух переменных, я постараюсь ограничиться самым минимумом. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.

Пример: 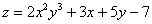– функция двух переменных.

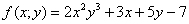
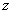
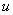
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .

С геометрической точки зрения функция двух переменных 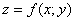чаще всего представляет собой поверхность трехмерного пространства (плоскость, цилиндр, шар, параболоид, гиперболоид и т. д.). Но, собственно, это уже больше аналитическая геометрия, а у нас на повестке дня математический анализ, который никогда не давал списывать мой вузовский преподаватель является моим «коньком».

Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:

…да, кстати, для этой темы я таки создал маленькую pdf-книжку, которая позволит «набить руку» буквально за пару часов. Но, пользуясь сайтом, вы, безусловно, тоже получите результат – только может чуть медленнее:

Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения:
или – частная производная по «икс»
или – частная производная по «игрек»

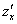
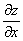
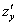
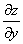
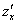
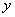
Начнем с . Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).

Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.

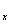
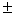
Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).

Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.

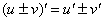
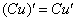
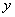
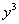
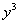
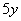
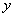
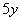
(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

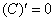
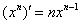
(3) Используем табличные производные и .

(4) Упрощаем, или, как я люблю говорить, «причесываем» ответ.

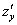
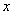
Теперь . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).

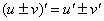
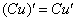
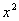
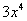
(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.

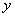
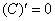
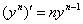
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива и для (да и вообще почти для любой буквы). В частности, используемые нами формулы выглядят так: и .

В чём смысл частных производных?

По своей сути частные производные 1-го порядка напоминают «обычную» производную:

– это функции, которые характеризуют скорость изменения функции в направлении осей и соответственно. Так, например, функция характеризует крутизну «подъёмов» и «склонов» поверхности в направлении оси абсцисс, а функция сообщает нам о «рельефе» этой же поверхности в направлении оси ординат.

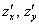
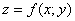
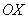
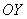
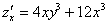
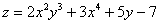
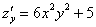
! Примечание: здесь подразумеваются направления, которые параллельны координатным осям.

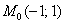
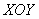
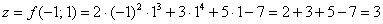
В целях лучшего понимания рассмотрим конкретную точку плоскости и вычислим в ней значение функции («высоту»):
– а теперь представьте, что вы здесь находитесь (НА САМОЙ поверхности).

Вычислим частную производную по «икс» в данной точке:

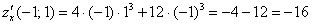
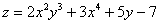
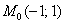
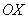
Отрицательный знак «иксовой» производной сообщает нам об убывании функции в точке по направлению оси абсцисс. Иными словами, если мы сделаем маленький-маленький (бесконечно малый) шажок в сторону острия оси (параллельно данной оси), то спустимся вниз по склону поверхности.

Теперь узнаем характер «местности» по направлению оси ординат: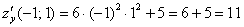

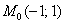
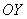
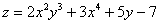
Производная по «игрек» положительна, следовательно, в точке по направлению оси функция возрастает. Если совсем просто, то здесь нас поджидает подъём в гору.

Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше по модулю – тем поверхность круче, и наоборот, чем оно ближе к нулю – тем поверхность более пологая. Так, в нашем примере «склон» по направлению оси абсцисс более крут, чем «гора» в направлении оси ординат.

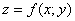
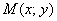
Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности по возможности в каждой точке области определения данной функции по всем доступным путям. Об этом и других интересных вещах я расскажу на одном из следующих уроков, ну а пока что вернёмся к технической стороне вопроса.

Систематизируем элементарные прикладные правила:

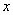
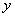
1) Когда мы дифференцируем по , то переменная считается константой.

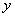
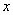
2) Когда же дифференцирование осуществляется по , то константой считается .

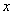
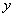
3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (, либо какой-нибудь другой), по которой ведется дифференцирование.

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения:
или – вторая производная по «икс»
или – вторая производная по «игрек»
или – смешанная производная «икс по игрек»
или – смешанная производная «игрек по икс»

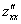
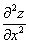
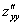
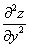
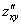
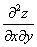
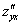
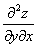
Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.

Для удобства я перепишу уже найденные частные производные первого порядка: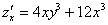

Сначала найдем смешанные производные:

Как видите, всё просто: берем частную производную 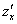и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

В практических примерах можно ориентироваться на следующее равенство:

Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».
Никаких изобретений, берем 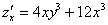и дифференцируем её по «икс» еще раз:

Аналогично:

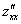
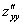
Следует отметить, что при нахождении , нужно проявить повышенное внимание, так как никаких чудесных равенств для их проверки не существует.

Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных. Но всему своё время:

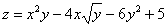
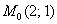
Вычислить частные производные первого порядка функции в точке . Найти производные второго порядка.

Это пример для самостоятельного решения (ответы в конце урока). Если возникли трудности с дифференцированием корней, вернитесь к уроку Как найти производную? А вообще, довольно скоро вы научитесь находить подобные производные «с лёту».

Набиваем руку на более сложных примерах:

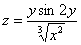
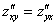
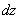
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .

Решение: Находим частные производные первого порядка:

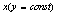
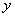
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.

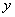
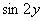
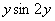
(1) Выносим все константы за знак производной. В данном случае и , а, значит, и их произведение считается постоянным числом.

(2) Не забываем, как правильно дифференцировать корни.

(1) Выносим все константы за знак производной, в данной случае константой является .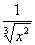

(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .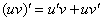

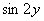
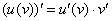
(3) Не забываем, что – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .

Теперь находим смешанные производные второго порядка:

, значит, все вычисления выполнены верно.

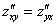
Запишем полный дифференциал 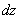. В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.

Полный дифференциал первого порядка функции двух переменных имеет вид:

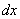
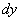
То есть, в формулу нужно тупо просто подставить уже найденные частные производные первого порядка. Значки дифференциалов и в этой и похожих ситуациях по возможности лучше записывать в числителях:

И по неоднократным просьбам читателей, полный дифференциал второго порядка.

ВНИМАТЕЛЬНО найдём «однобуквенные» производные 2-го порядка:

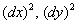
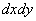
и запишем «монстра», аккуратно «прикрепив» квадраты , произведение и не забыв удвоить смешанную производную:

Ничего страшного, если что-то показалось трудным, к производным всегда можно вернуться позже, после того, как поднимите технику дифференцирования:

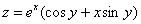
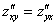
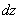
Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .

Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.

Рассмотрим серию примеров со сложными функциями:

Найти частные производные первого порядка функции .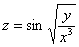
Записать полный дифференциал .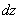

Решение:

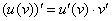
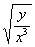
(1) Применяем правило дифференцирования сложной функции . С урока Производная сложной функции следует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение (внутренняя функция) у нас не меняется.

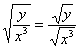
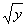
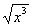
(2) Здесь используем свойство корней: , выносим константу за знак производной, а корень представляем в нужном для дифференцирования виде.

Аналогично:

Запишем полный дифференциал первого порядка:

Найти частные производные первого порядка функции .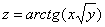
Записать полный дифференциал .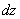

Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое

Довольно часто все вышерассмотренные правила применяются в комбинации.

Найти частные производные первого порядка функции .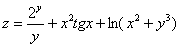

(1) Используем правило дифференцирования суммы

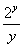
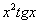
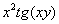
(2) Первое слагаемое в данном случае считается константой, поскольку в выражении нет ничего, зависящего от «икс» – только «игреки». Знаете, всегда приятно, когда дробь удается превратить в ноль). Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в этом смысле ничего бы не изменилось, если бы вместо была дана функция – важно, что здесь произведение двух функций, КАЖДАЯ из которых зависит от «икс», а поэтому, нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.

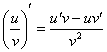
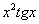
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: . Второе слагаемое зависит ТОЛЬКО от «икс», значит, считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.

Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки:

Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:

– А почему это ты от меня никуда не убегаешь?

– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!

На что злобная производная с коварной улыбкой отвечает:

– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.

Кто понял анекдот, тот освоил производные, минимум, на «тройку»).

Найти частные производные первого порядка функции .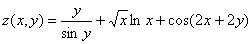

Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.

Ну вот почти и всё. Напоследок не могу не обрадовать любителей математики еще одним примером. Дело даже не в любителях, у всех разный уровень математической подготовки – встречаются люди (и не так уж редко), которые любят потягаться с заданиями посложнее. Хотя, последний на данном уроке пример не столько сложный, сколько громоздкий с точки зрения вычислений.

Дана функция двух переменных 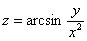. Найти все частные производные первого и второго порядков.

Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.

Что дальше? Дальше знакомимся с родственной темой – частными производными функции трёх переменных. После этого я рекомендую ДОБРОСОВЕСТНО (жить будет легче ;)) отработать технику дифференцирования на уроках Производные сложных функций нескольких переменных, Как проверить, удовлетворяет ли функция уравнению? и Частные производные неявно заданной функции. И, наконец, обещанная вкусняшка – Производная по направлению и градиент функции. Стратегия и тактика знакомы – сначала учимся решать, затем вникаем в суть!

Пример 2: , , , ,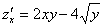
, , .

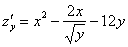
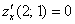
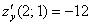
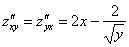
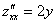
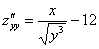
Пример 4: Ссылка для просмотра или скачивания ниже.

Пример 6: , ,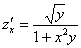

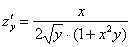
Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник